DSP实验三 离散系统的频率响应分析和零、极点分布

实验目的：加深对离散系统的频率响应分析和零、极点分布的概念理解。

实验原理：离散系统的时域方程为

在MATLAB中，可以用函数[z，p，K]=tf2zp（num，den）求得有理分式形式的系统转移函数的零、极点，用函数zplane（z，p）绘出零、极点分布图；也可以用函数zplane（num，den）直接绘出有理分式形式的系统转移函数的零、极点分布图。

另外，在MATLAB中，可以用函数 [r，p，k]=residuez（num，den）完成部分分式展开计算；可以用函数sos=zp2sos（z，p，K）完成将高阶系统分解为2阶系统的串联。

补充：tf2zp全称是Convert transfer function to zero-pole-gain form。使用范式[z,p,k]= tf2zp(b,a)，H(s)是传递函数，b代表分子系数数组，a代表分母系数数组。tf2zf函数的作用就是把上式的H(s)转换为下面这种表现形式：

zplane(z, p)绘制出列向量z中的零点（以符号“○” 表示）和列向量p中的极点（以符号“×”表示），同时画出参考单位圆，并在多阶零点和极点的右上角标出其阶数。zplane(b, a)绘制出系统函数H(z)的零极点图。

Z--zero P-- pole

[r，p，k]=residuez（b，a）z^-1形式的展开式

输出r p k的值代表部分分式展开后的 分子 分母 常数项（其中分子分母一一对应）留数r极点p多项式k

[r，p，k]=residue（b，a）是以z形式展开

实验内容：求系统

  的零、极点和幅度频率响应。

clc;
b=[0.0528 0.0797 0.1295 0.1295 0.797 0.0528];
a=[1 -1.8107 2.4947 -1.8801 0.9537 -0.2336];
subplot(311);
zplane(b,a);

[r,p,k]=residuez(b,a);
fs=-pi:pi/100:pi;
H=freqz(b,a,fs);
%计算数字滤波器的频率响应[H, f] = freqz(b, a, n, fs) 
%：n:频率响应点数。默认为 512 ；fs：数字滤波器的采样频率。默认为 2π。
%返回参数H：数字滤波器的复频率响应；f：数字滤波器的频率向量，单位为 Hz。
subplot(312),plot(fs,abs(H))
title('幅度响应曲线')
subplot(313),plot(fs,180/pi*unwrap(angle(H)));
title('频率响应曲线')
%卷绕：若一个角度从0变到2pi，但实际得到的结果是0～pi，再由-pi～0，在w=pi处发生跳变，跳变幅度为2pi，这就叫相位的卷绕。
%unwrap（w）反正切函数：解卷绕，使相位在pi处不发生跳变，从而反应出真实的相位变化。
%theta = angle(z)为复数数组 z 的每个元素返回区间 [-π,π] 中的相位角。
%theta 中的角度表示为 z = abs(z).*exp(i*theta)。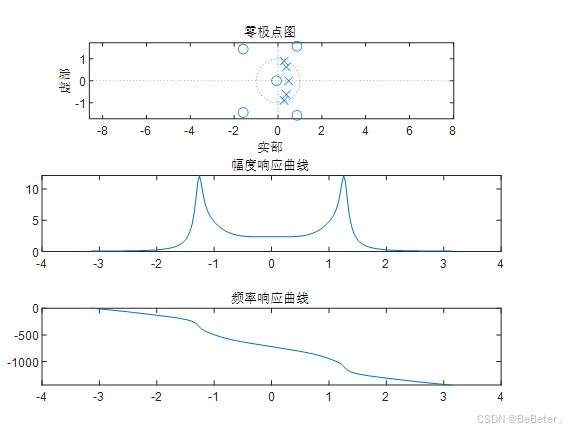

实验要求：编程实现系统参数输入，绘出幅度频率响应曲线和零、极点分布图。