使用LTSpice进行最坏情况分析

使用LTSpice进行最坏情况分析

在一些电路设计场合，如差分放大电路、恒流源、精密采样电路等，对于部分无源器件的自身精度有着特殊的要求。出于电路成本和设计难度的考虑，需要考虑无源器件标称值的不确定度是否满足电路设计需求。因此，需要对相关电路进行最坏情况分析。

SPICE提供了相关语句，方便电路设计者进行最坏情况分析。但是，在LTSpice中.WCASE并未提供。因此，需要采用曲线救国的方式进行最坏情况分析。

电路原理图

首先，给出演示用的电路原理图，相关的运行指令也在图中。该电路来自于ADI的技术文章LTspice: Worst-Case Circuit Analysis with Minimal Simulations Runs。图中所给出的是一个典型的差动放大器。

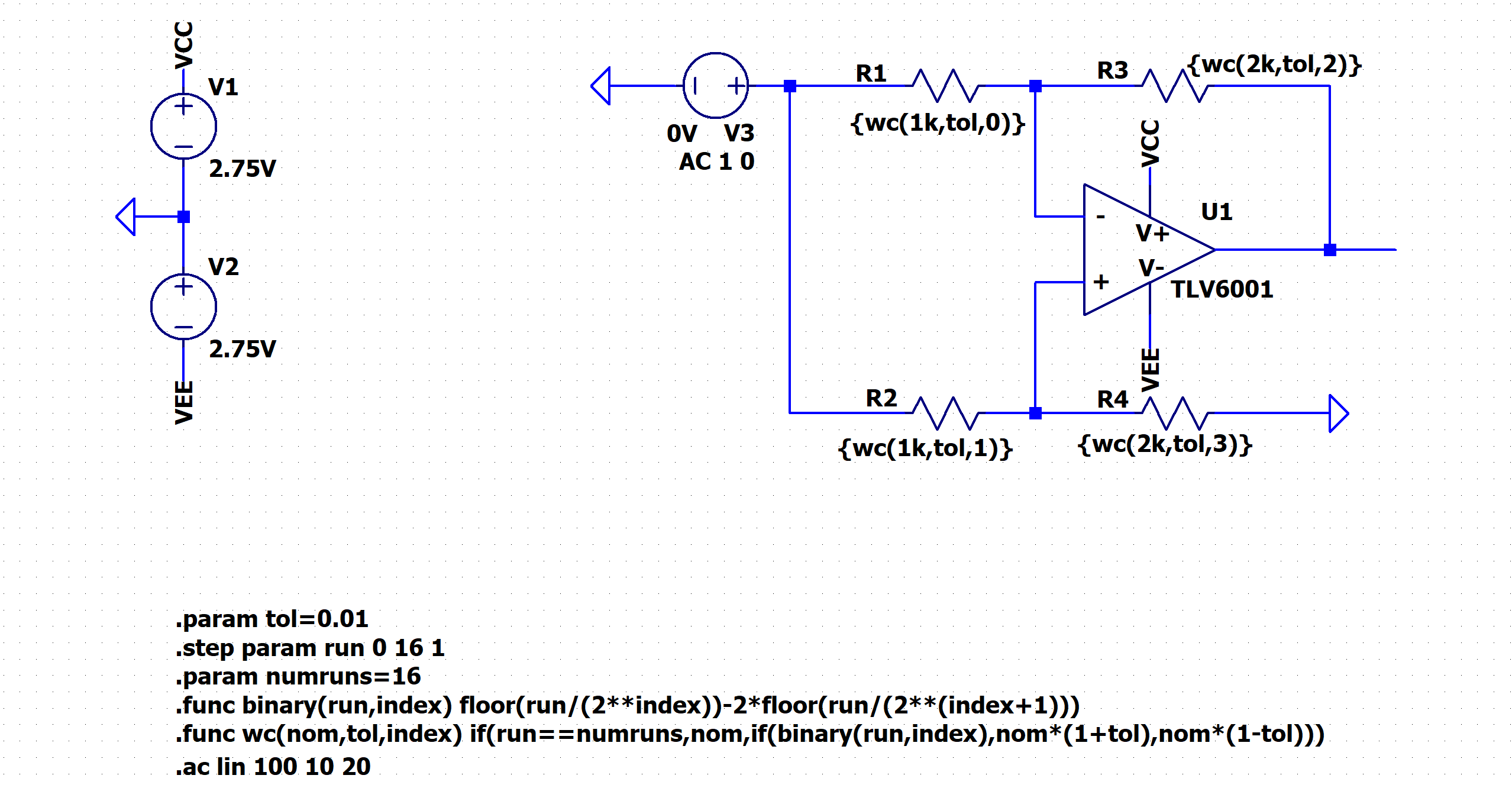
仿真运行原理

假设器件的标称值为val，精度是tol，那么器件的实际值属于$[\mathrm{val}\ast (1-\mathrm{tal}),\mathrm{val}\ast (1+\mathrm{tal})]$这一区间内。那么电路运行的最坏情况只有可能在器件的实际值等于$\mathrm{val}\ast (1-\mathrm{tal})$或$\mathrm{val}\ast (1+\mathrm{tal})$的情况下出现。因此，只需要对所有器件的最大最小值进行排列组合，并对所有情况做交流或直流分析就能得到电路的最坏情况分析结果。
对于N个待分析的器件，所需要进行的分析次数为$2^{\mathrm{N}}$次，图中代码还分析了最理想的情况（所有器件的值皆为标称值），因此图中的仿真代码的实际运行次数是$2^{\mathrm{N}}+1$次。这段代码的精华部分在于利用LTSpice提供的函数，依据二进制的思想，实现元器件实际值的排列组合，对应的代码就是自定义函数binary。

相关命令解释

.param

这个指令的功能是定义一个常数。如图中所示的两行:

.param tol=0.01
.param numruns=16

这里分别定义了两个参数tol和 numruns。其中tol用来表示器件的精度。numruns顾名思义表示的运算次数

.step

这个指令类似于for循环，在一个范围内按规定步长步进。

.step param run 0 16 1

以上命令的功能是让参数run从0变化到16，步长为1。

.ac

这个命令想必并不陌生，他就是进行交流仿真的命令，如图中所示：

.ac lin 100 10 20

这句话的意思就是从10Hz~20Hz进行线性的交流扫描，扫描点数为100个点。

.func

该命令用于创建自定义函数。这里定义了两个自定义函数，用于设置器件的参数值。

wc函数

首先来看第一个最外层的函数wc，其定义如下

.func wc(nom,tol,index) if(run==numruns,nom,if(binary(run,index),nom*(1+tol),nom*(1-tol)))

该函数的返回值是器件的值，值的选取是由仿真的次数来确定的。该函数拥有三个形参：

• nom：元器件的标称值
• tol：元器件的精度
• index：元器件的编号（从0开始，不能重复）

该函数的执行逻辑流程图如下：

binary函数

再来看一下嵌套在wc函数内部的函数binary，其定义如下：

.func binary(run,index) floor(run/(2**index))-2*floor(run/(2**(index+1)))

该函数里调用了一个系统函数floor，其定义如下：

floor(x): Integer equal to or less than x

返回值是不超过输入变量的最大整数。

binary设计的核心思想是在进行最坏情况分析时，每个器件实际上只有两个取值（最大或最小的情况），可以用0和1来表示。假设有N个器件，对器件的取值进排列组合，一共有$2^{\mathrm{N}}$种情况，因此需要进行$2^{\mathrm{N}}$次仿真。仿真次数正好可以使用二进制来表示，假设器件的值为 v n ∈ { 0 , 1 } v_{n}\in\{0,1\} vn​∈{0,1}，器件的编号记为 n ∈ { 0 , 1 , … , N − 1 } n\in\{0,1,\dots,\mathrm{N-1}\} n∈{0,1,…,N−1}，则运行的次数numruns可以满足：
$$\mathrm{numruns}=\sum _{n=0}^{\mathrm{N}-1}{v}_n\cdot 2^n$$
现在问题转换为已知$\mathrm{numruns}、n$求$v_n$的值。用第n位的位权整除numruns去除低位的所有信息，再用第n+1位的位权整除numruns得到高位的所有信息，二者相减就能得到第n位上的值。用公式表示如下：
$$v_n=\lfloor \frac{\mathrm{numruns}}{2^{\mathrm{N}}}\rfloor -2\times \lfloor \frac{\mathrm{numruns}}{2^{\mathrm{N}+1}}\rfloor$$
在本次的案例中，进行的16次仿真中，各器件的取值变化如下表：

run	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
index 0	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
index 1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
index 2	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
index 3	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1

仿真结果

最后，运行仿真，可以得到如下结果：