利用运动学实现导弹仿真飞行

利用Unity实现导弹飞行的算法网上案例很多，本篇博客主要给读者介绍如何将所学算法运用到项目开发的实战教程。
我们将使用运动学原理实现仿真，这意味着我们将只在计算中使用速度，而不考虑物体上的质量和其他作用的物理力，这些力会影响物体的运动，比如阻力。为了能够模拟导弹击中目标，我们将考虑以下变量:
发射速度，发射角度，导弹距离目标的距离。
很多程序员学过算法，学过数据结构，但是在项目开发过程中就不会灵活运用了，所以有些人觉得以前学的知识没用，其实这是完全错误的，大学读书的过程也是一种培养能力的过程，大学所学的都是一些基础知识，他也是为我们以后能够自学打下基础。而且大学学习的算法在游戏开发中用的非常多，我们也借助本篇博客告诉读者如何将所学知识应用到项目开发中。
下面我们就围绕算法讲解实现过程：
我们将从运动的运动学方程开始，其实也就是我们说的抛物线方程，它描述了基于初始速度和加速度所获取到的位置:

P1是最后的位置，P0是初始位置，v0初始速度，a加速度，t是运动持续时间。我们在纸上推导一下数学公式，看能到什么结果？

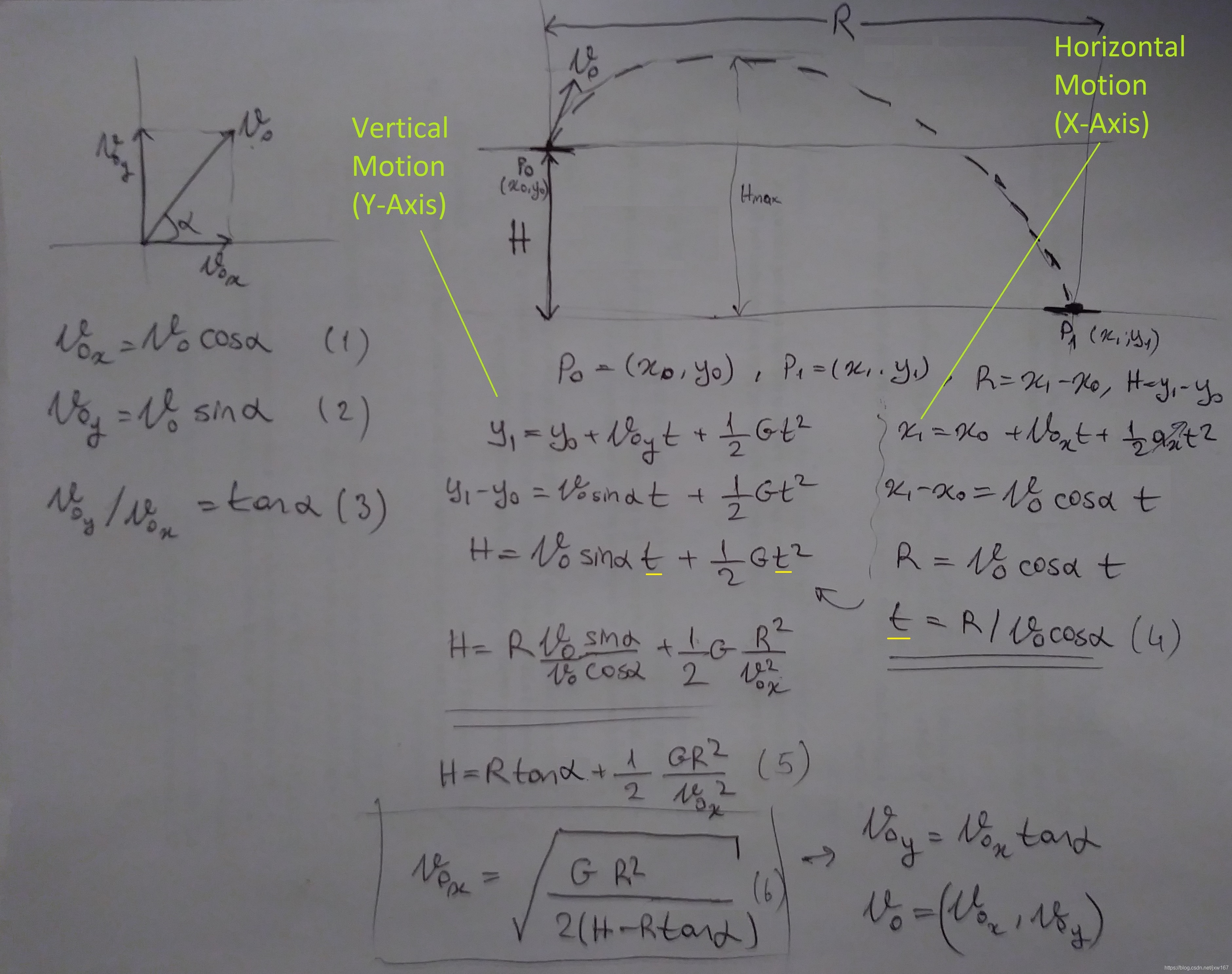
a是发射角度，V0是初始速度，V0x，V0y是初始速度V0的两个分量，H是沿着y轴位置距离差，R是沿x轴的位置距离差，t就是抛物线运动的时间。
通过我们的推演可以知道以下几个条件：一是，在x轴的运动距离是R，初始速度是V0x，运行时间是t；二是，在y轴运动距离是H，初始速度是V0y，重力G以及运行轨迹的时间t；三是，沿着y轴的距离H, x轴R, G重力，发射角α和初速度V0x也就是V0的分量。利用我们的这些已经计算好的公式，最终推导出上图的公式如下所示：

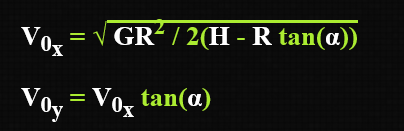
在解答方程之前，我们还要解决一个问题就是导弹朝向目标问题，在Unity中提供了LookAt函数，再思考目标物体和导弹的高度不同的情况，虽然我们希望在下面的gif中使用左边的效果，但是如果使用LookAt()函数，我们将获得右边的效果。

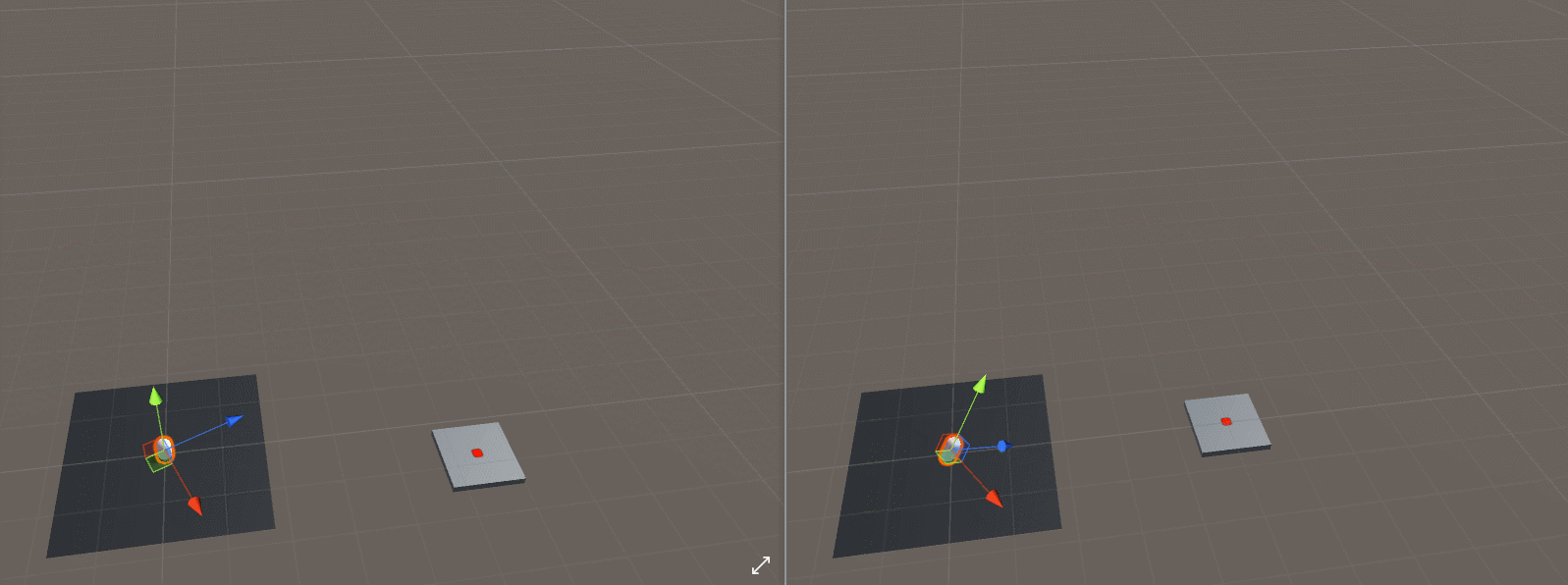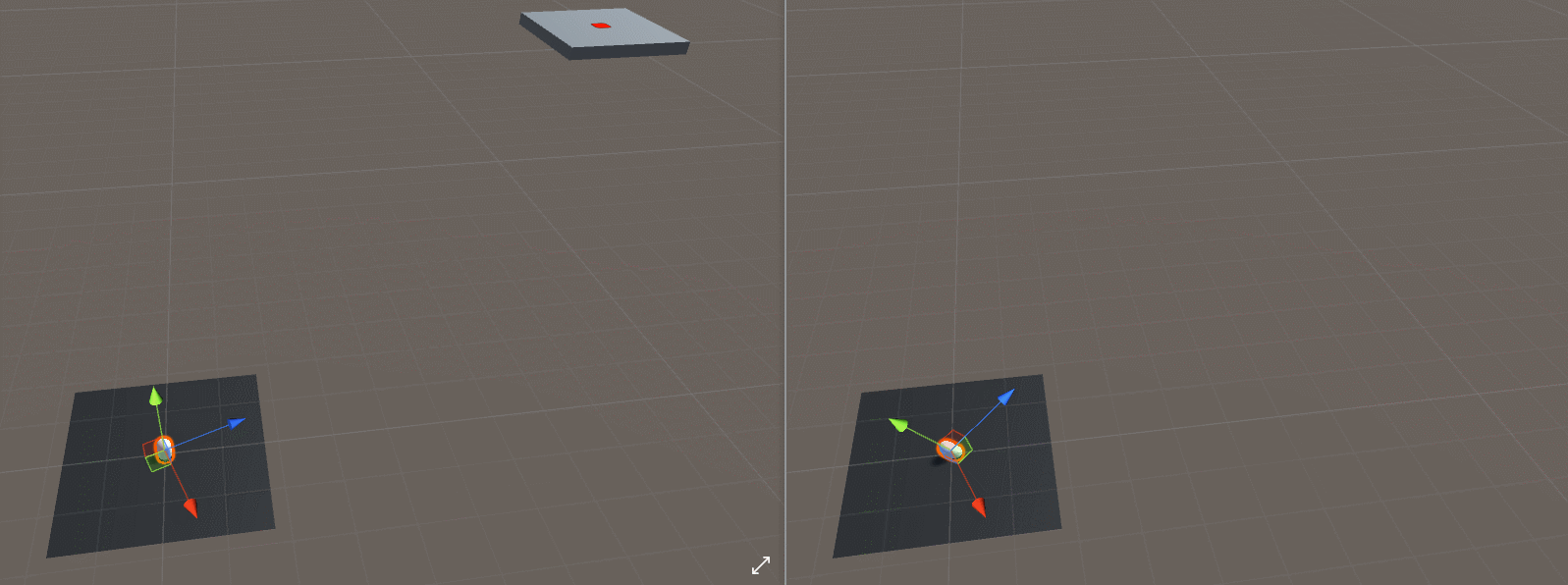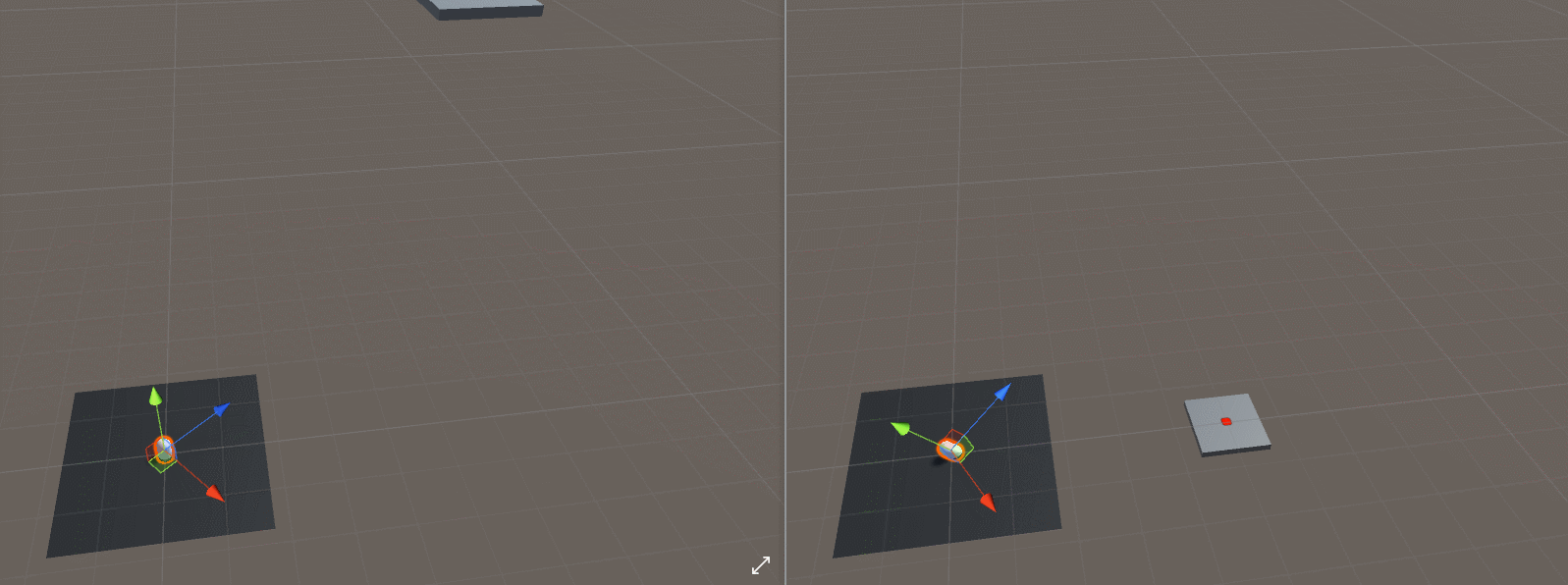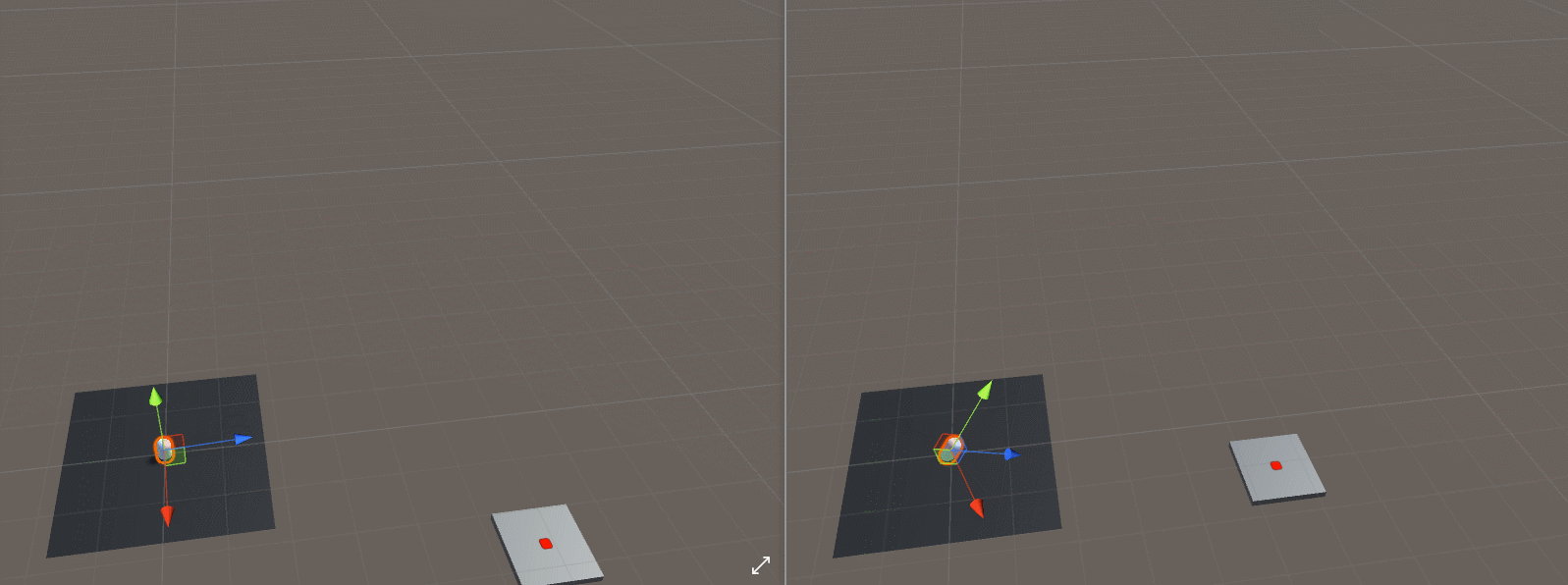
如果我们像这样放弃目标的Y分量和抛射体的位置，我们可以达到预期的“转向”效果，代码如下所示：

void Launch()
{
    // think of it as top-down view of vectors: 
    //