【扩散模型核心思想讲解】李宏毅 2023 最新 Diffusion Model 原理讲解

kebijuelun

已于 2024-07-11 18:19:42 修改

阅读量7.1k

点赞数 35

文章标签：人工智能 AIGC stable diffusion

于 2024-04-14 18:46:50 首次发布

本文链接：https://blog.csdn.net/kebijuelun/article/details/137739340

版权

Diffusion Model 概念讲解

基本原理介绍

Diffusion 定义与应用

Diffusion Model（扩散模型）是一种深度学习算法，主要用于生成模型领域，尤其在图像生成中取得了显著的成果。这种模型的核心思想是模拟一个从有序到无序再到有序的扩散过程，通过逐步增加然后再逐步去除噪声的方式来生成数据。
- 应用：扩散模型在多种数据生成任务中表现出色，例如图像生成、音频合成和文本生成等。在图像生成方面，扩散模型能够生成高质量、高分辨率的图像，竞争力甚至超过了其他类型的生成模型，如生成对抗网络（GANs）。

原理

Diffusion Model
- 扩散模型包括两个主要的阶段：前向扩散阶段和反向扩散（或去噪）阶段。
  - 前向扩散阶段：在这一阶段，模型将逐步向原始数据添加噪声，使数据从有序状态变成几乎完全随机的噪声状态。这个过程通常是预定的并遵循特定的噪声增加路径。
  - 反向扩散阶段：这一阶段是扩散模型的核心，模型将逐步从噪声数据中恢复出原始的有序数据。在这个过程中，模型学习如何有效地从包含高比例噪声的数据中恢复出干净的数据。这一阶段通常需要通过训练一个深度神经网络来实现。

推理阶段

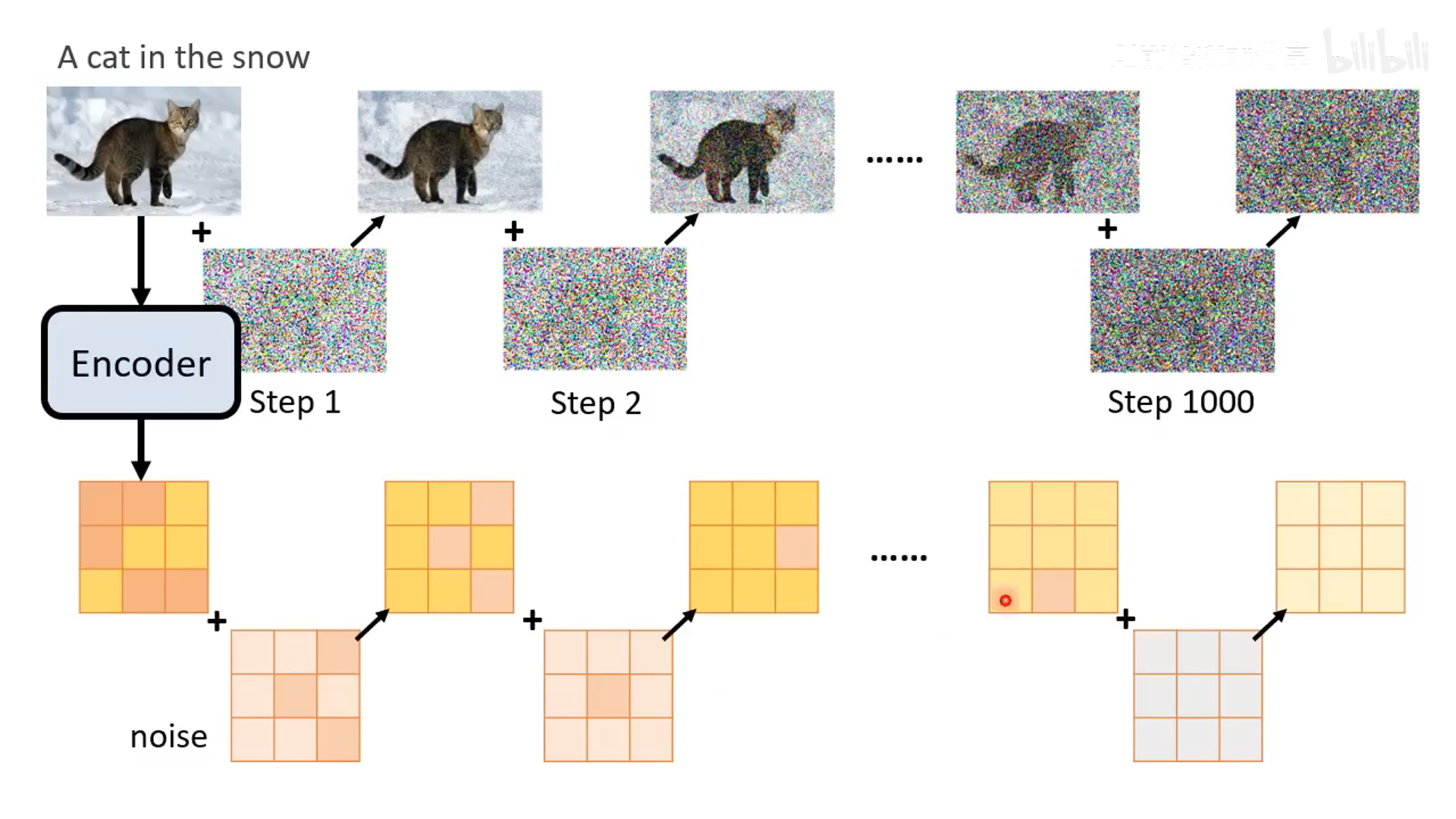
降噪过程，基于一个 denoise 模型来做，除了吃输入的带噪声的图片还要输入当前的降噪步数 t。比如 1 step 的噪声较少，1000 step 的噪声很多
denoise 模块内部是预测噪声，然后减去噪声。预测噪声的难度比预测去噪后的图像的难度不一样，预测噪声更简单

训练阶段

训练阶段加噪声
输入是带噪声的图，预测的输入是该时间步加上的噪声

text to image

text to image 的训练需要大量的文本图像对数据。和 LAION 数据比起来，ImageNet 的数据量算很小的
需要把文字也输入给 Diffusion 模型
text to image 的训练 loss 如下

训练推理算法

在这里插入图片描述

Diffusion 主流方法

latent diffusion model （典型工作是 Stable Diffusion）

latent diffusion model：与传统 Diffusion 不一样的是在 latent 的隐状态空间进行 diffusion 操作，通过 VAE 编码的 latent 训练，推理阶段通过 VAE 解码的图像作为最终结果。以下三个 model (text encoder， generation model，decoder) 一般是分开训练的。
stable diffusion 也是类似这样 latent diffusion model 的形式
OpenAI 的 DALL-E 做法也类似，不过 generation 步骤同时尝试了 Autoregressive 和 Diffusion 两种方式。这两种方式在效果上差异不大，但是 Diffusion 在训练效率上优于 Autoregressive (AR) 。因此，最终 DALL·E 2 选择 Diffusion。
Google Imagen 的套路也基本一样，多的是加了个 diffusion 的 SR 模型进行高清化上采样

三个主要模块介绍

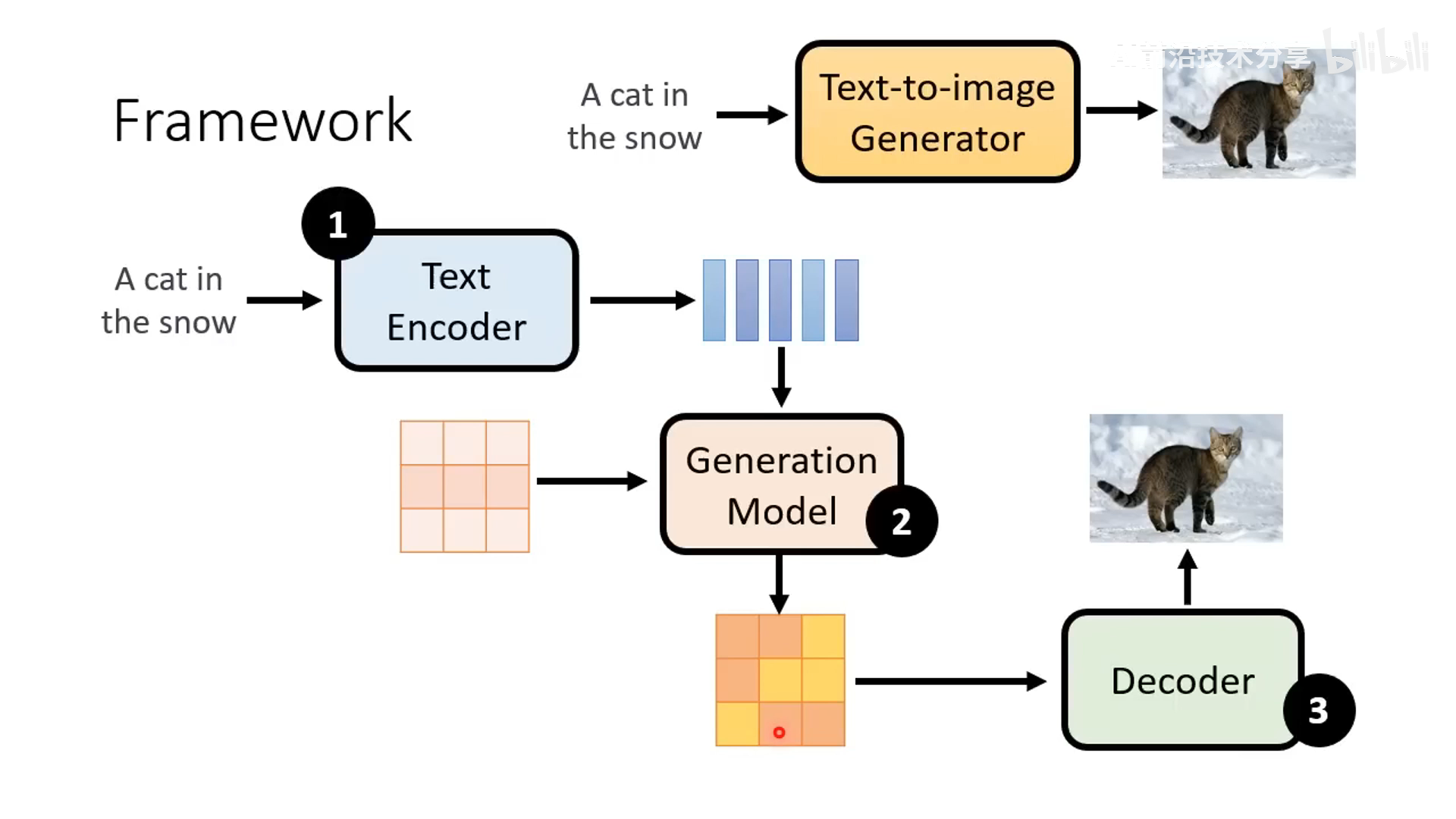
在这里插入图片描述

Text encoder

text encoder 介绍（来源 Imagen），encoder 对结果影响很大。FID 越小越好，CLIP Score 越大越好，所以在图像中偏右下角会更好，随着 encoder 参数量变大，效果逐渐变好。
FID 介绍，利用一个模型分别提取真实图像和生成图像的特征，假设这两组特征的分布为高斯分布，然后算这两组分布的距离，这个距离越小说明生成的图像越接近真实图像。
CLIP 介绍：基于大规模的图文对数据训练，分辨图像和文本是否接近。CLIP score 越大越好

Decoder

训练 auto-encoder，encoder 将图像编码为 latent，decoder 将 latent 恢复为原始图片

generation

在 latent 层面上进行加噪声
loss 计算方式与之前的图像层面的一致，只是输入图片变为了输入 latent
推理阶段就是从高斯分布采样一个噪声，与文本输入后不断降噪得到生成的 latent，latent 经过 decoder 后得到预测图片

Diffusion 数学原理

Diffusion 算法流程的介绍

具体讲解算法的数学原理

VAE 与 Diffusion Model 区别

整体形式比较接近，diffusion 的 add noise 对应于 VAE 的 encoder，去噪类似 VAE 中的 decoder

Training

训练集中抽一个 clean image x0，然后采样一个高斯噪声 $\epsilon$ ，采样一个时间步数 t。以上信息输入 noise predicter，得到预测的噪声与采样得到的 $\epsilon$ 计算 loss
这里和之前所说的要从 1-1000 一步步加噪声和降噪不一样，而是一步加噪声和降噪声。这一步数学原理比较复杂，后续会详细讲解。

推理阶段

循环 T 步，不断降噪。这里比较奇怪的是每个迭代都需要采样一个噪声来加到降噪后的图像上得到最终预测的降噪图像，这里后续会介绍原因

具体数学原理

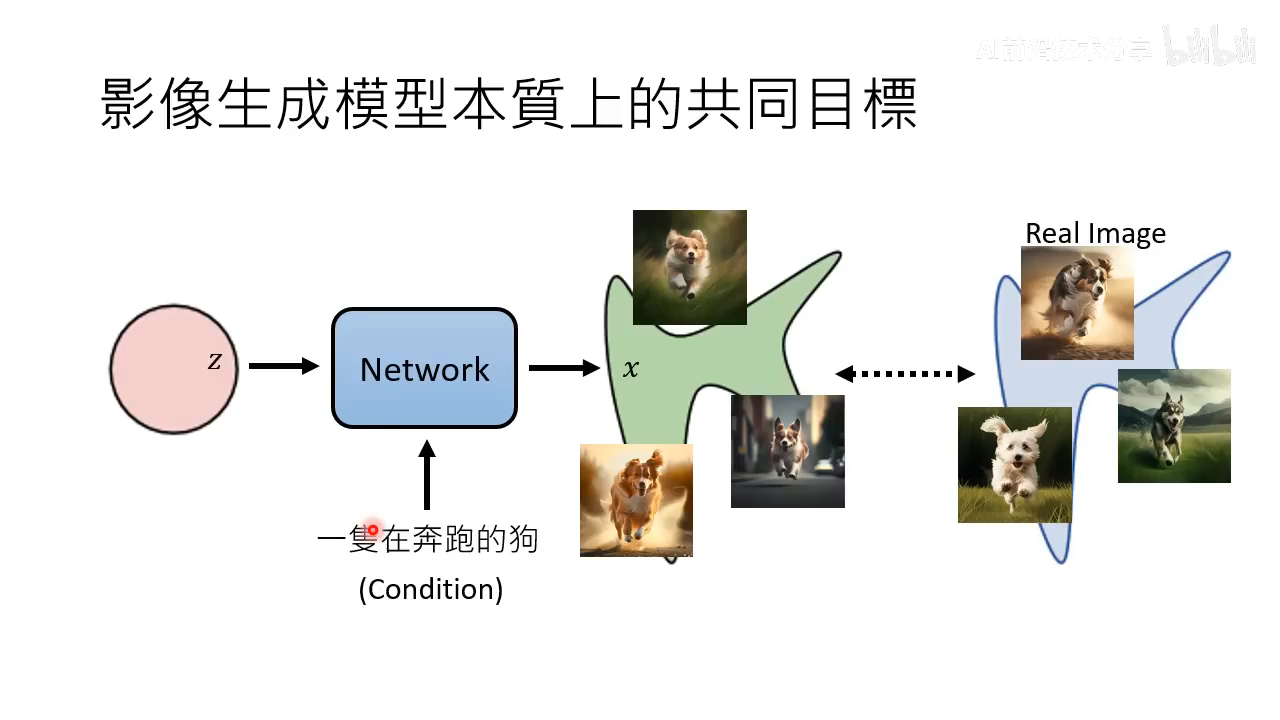
图像生成模型的目标

图像生成模型的共同目标：生成图像分布与真实图像分布尽量一致
在增加 condition 的情况下本质上还是一样的目标
maximum likelihood estimation 用于让生成的分布尽量和真实的分布接近。在真实分布中采样一批图片，找一个模型参数 $\theta$ 让生成真实图片 x1,…, xm 的概率最大
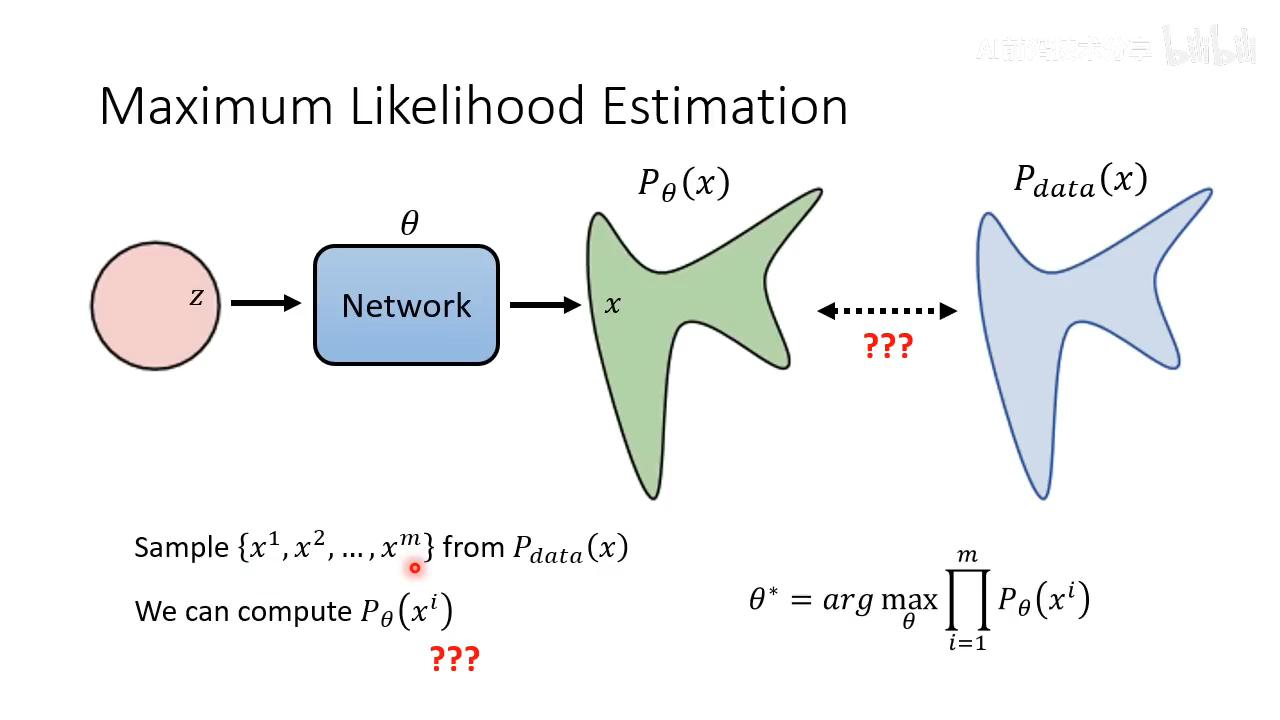
推导可以发现以上计算最大似然等价于最小化 KL Divergence，这个也就其实等价于让生成的分布和真实图像分布尽量接近

diffusion model 是 maximum likelihood，GAN 是 minimize Divergence

VAE

VAE 如果直接预测 $P_{\theta}(x)$ 比较困难，所以预测 Mean of Gaussian
VAE 一般是通过 maximize lower bound 的方式来训练

DDPM 数学原理推导

DDPM 计算 $P_{\theta}(x)$ (下标中有 $\theta$ 代表通过模型计算 ) 的方式，对所有可能的 xt 做积分。
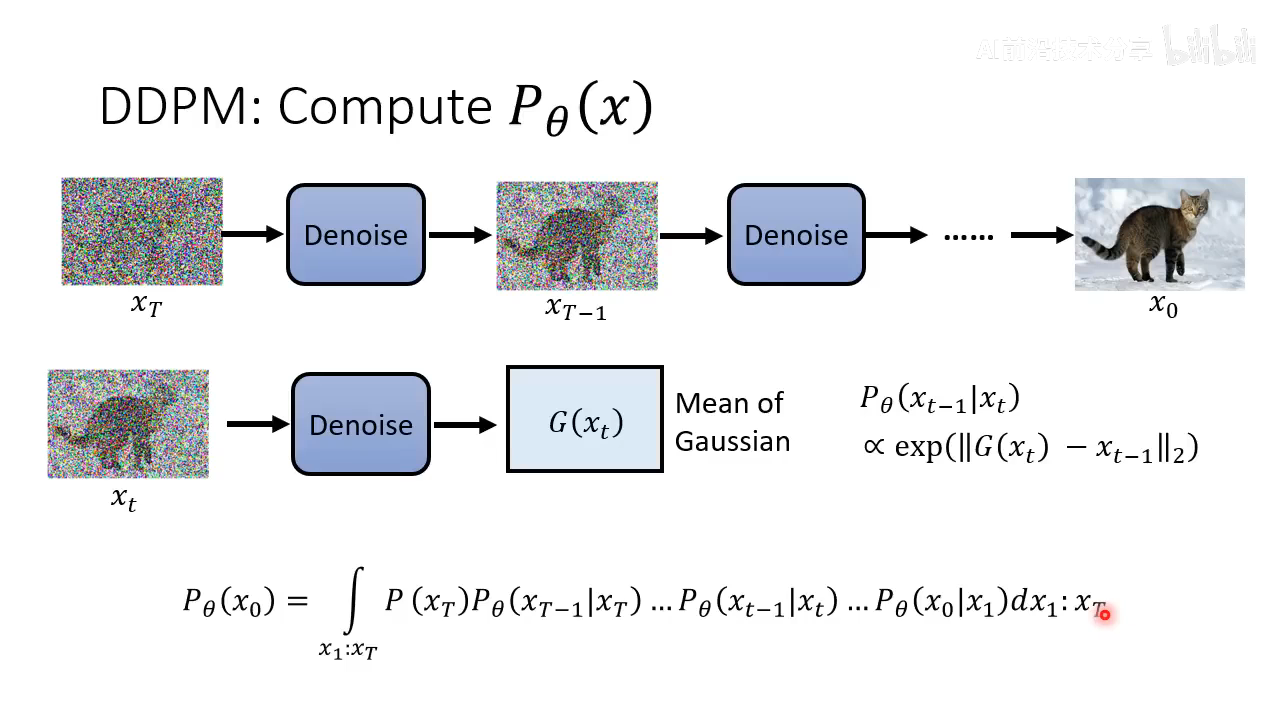
DDPM 对比 VAE，目标很接近。VAE Encoder 对应于 Diffusion 的 forward 过程
计算 $q(x_{t}|x_{(t-1)})$ 的方式，这个 $q(x_{t}|x_{(t-1)})$ 依然是高斯分布，mean 是 $\sqrt{1-{\beta}_{t}}$ ，variance 就是 $\beta_{t}$ 。这里从 $x_0$ 到 $x_t$ 可以如图中这样一步一步计算得到
以上 $x_0$ 到 $x_t$ 也可以一步计算得到。因为每次加的高斯噪声是独立同分布的：

2 步采样等同采样 1 步的结果的方式

t 步的采样也可以等价于 1 步采样。将 $\beta$ 讲话为用 $\alpha$ 表示
推导 diffusion 的优化目标，比较复杂老师不仔细讲，直接给出结果

继续上面的推导结果。第二项不用管，因为和 network 的参数没有关系，因为是 $x_T$ 是直接高斯分布采样得到的，q 也是人工定义好的 diffusion process，和 network 无关。

主要将第三项如何推导，第一项和第三项比较像。

$q(x_{t-1}|x_{t}, x_{0})$ 这个之前没有讲过如何计算，计算方式如下

经过一些推导之后，结果依然是一个高斯分布

均值和方差为

两个高斯分布的 KL 散度是有公式解的，可以用公式计算。不过这里不用直接计算出来，因为这里不考虑 diffusion 的方差，直接让两个高斯分布的 mean 接近就行

实际上的操作如下，让 diffusion 模型的输出分布的 mean 和 $q(x_{t-1}|x_{t}, x_{0})$ 的 mean 尽量接近

这个过程的可视化如下

化简掉 $x_0$

这里模型唯一需要预测的就是 $\epsilon$ ，这样就推导出了 sampling 的算法公式了

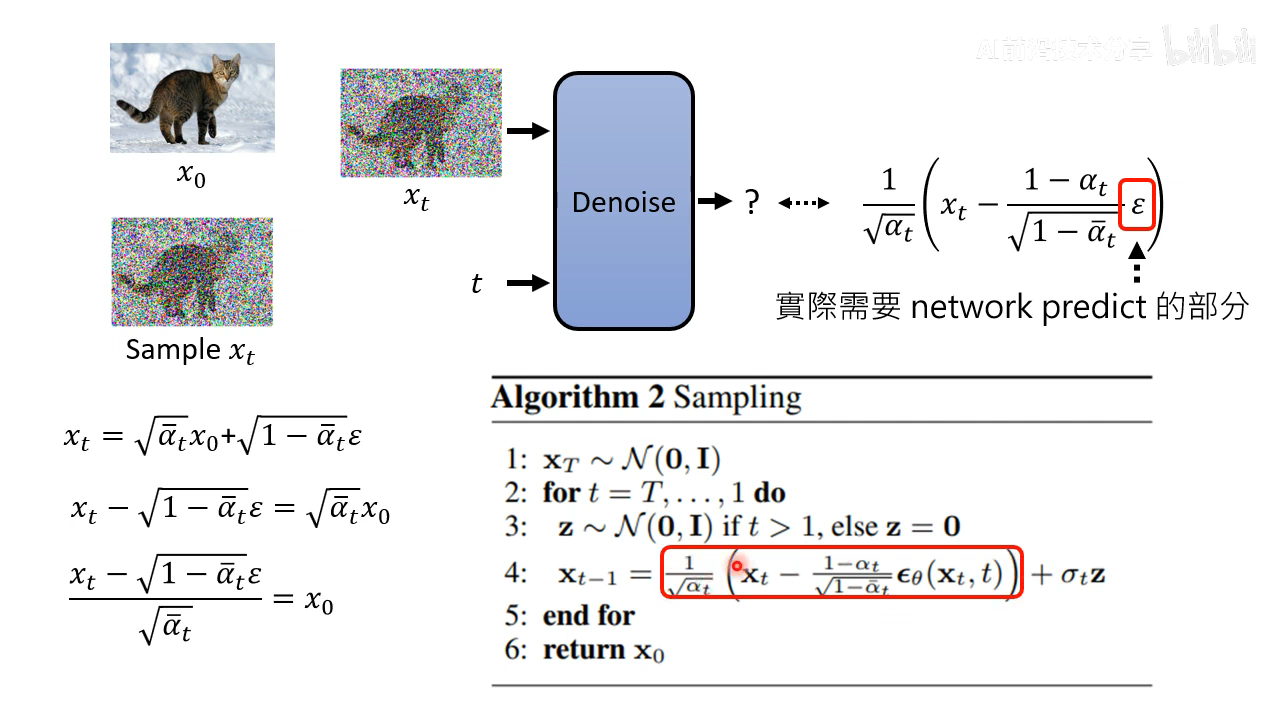
数学原理讨论

sampling 为什么要加 noise 项

这里有个问题是为什么要多加一个 noise 项，这个原因是网络预测的是 Mean of Gaussian，所以要加一个 noise 项重新 sample 为高斯分布。这就引出问题：为什么不直接取 Mean？
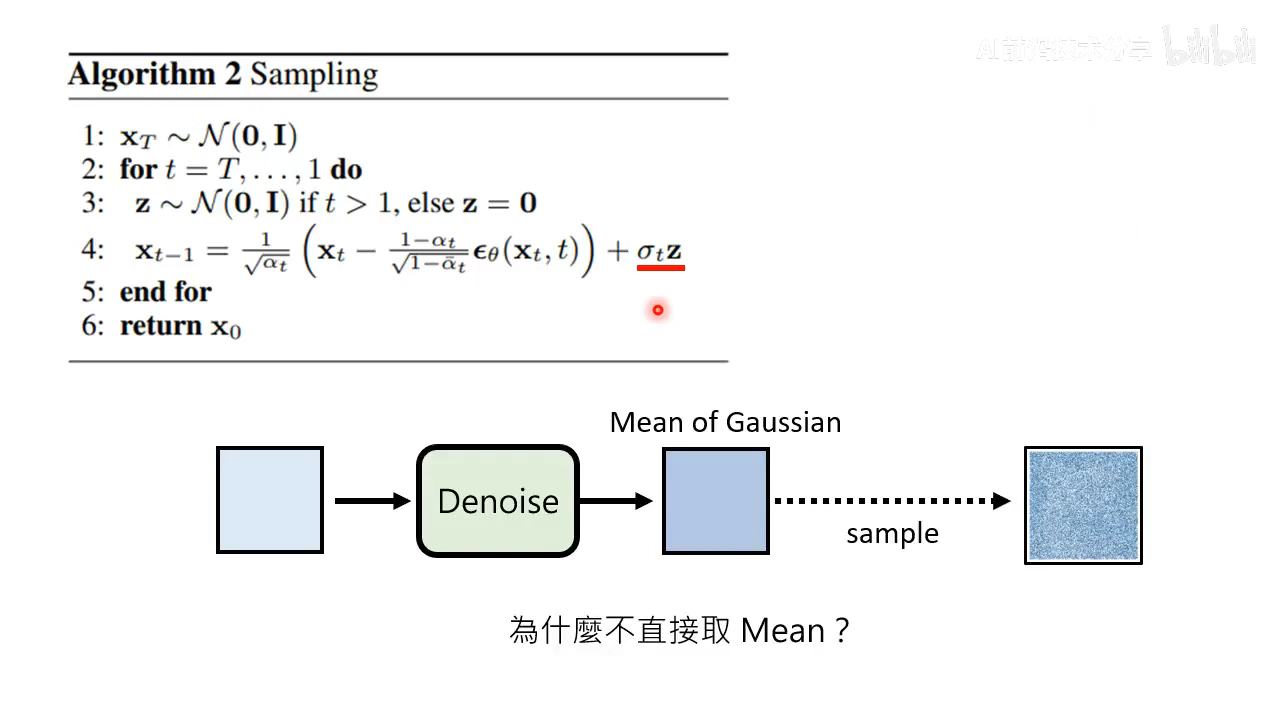
在这里插入图片描述
该问题暂时没有定论，以下是李宏毅老师的猜测。认为这和 LLM 要 sample 很类似

取几率最大的，最后结果容易重复，sample 结果更好

人写的文章并不是选几率最大的，人生成的文本的效果更好，所以需要 sampling 过程
在这里插入图片描述
语音合成也是需要 sampling 才行

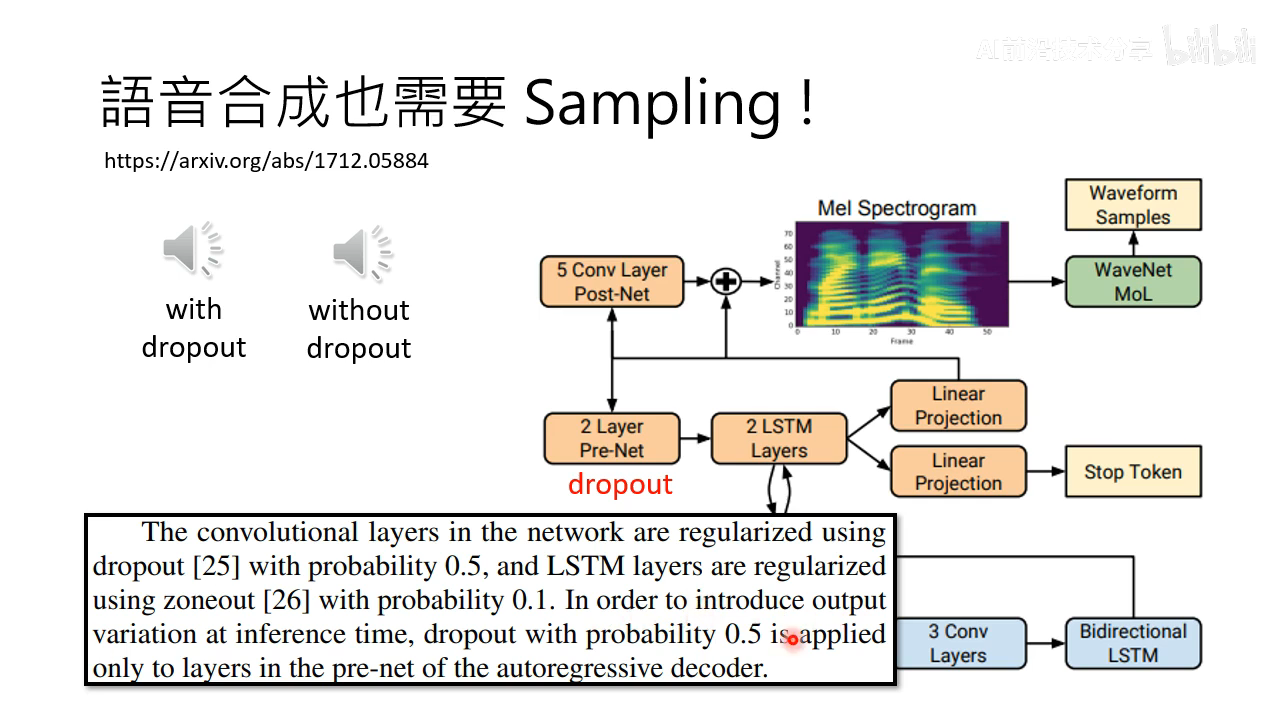
如果不加 noise 效果不好
在这里插入图片描述

diffusion 应用讨论

diffusion 模型用于语音，流程与 DDPM 没有太大区别，2d noise 替换为 1d noise
diffusion 模型用于文本。难点是不能直接应用 DDPM，因为文本是离散的，无法加 noise 到看不出来文本信息的高斯分布。解决方法是在 latent space 上来加高斯分布

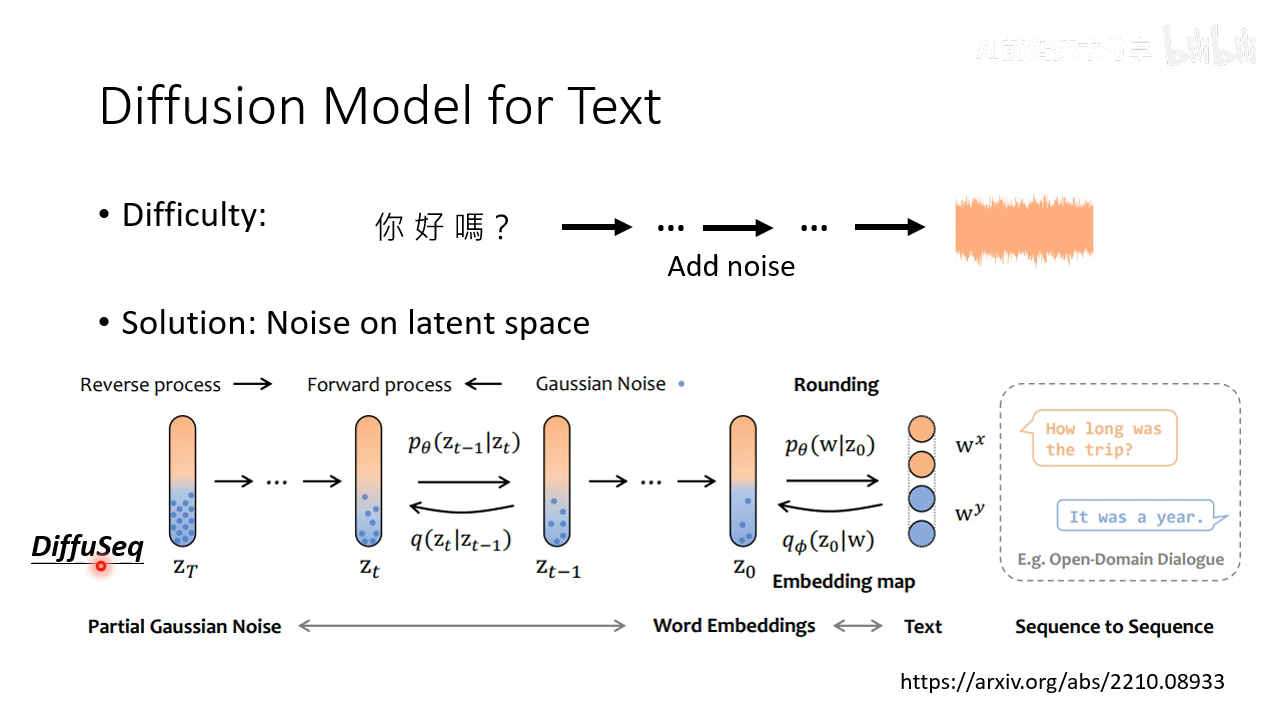
还可以不加高斯分布，比如 noise 是加 [MASK]

Diffusion 成功的原因分析

diffusion model 也是一种 autoregressive model

diffusion model 也是一种 autoregressive model，每次 denoise 看成是 autoregressive 中的一步
各个击破 + N 次到位

和 mask-predict 很像，也是多次生成的方式

把几率比较低的 mask 掉再做一次生成

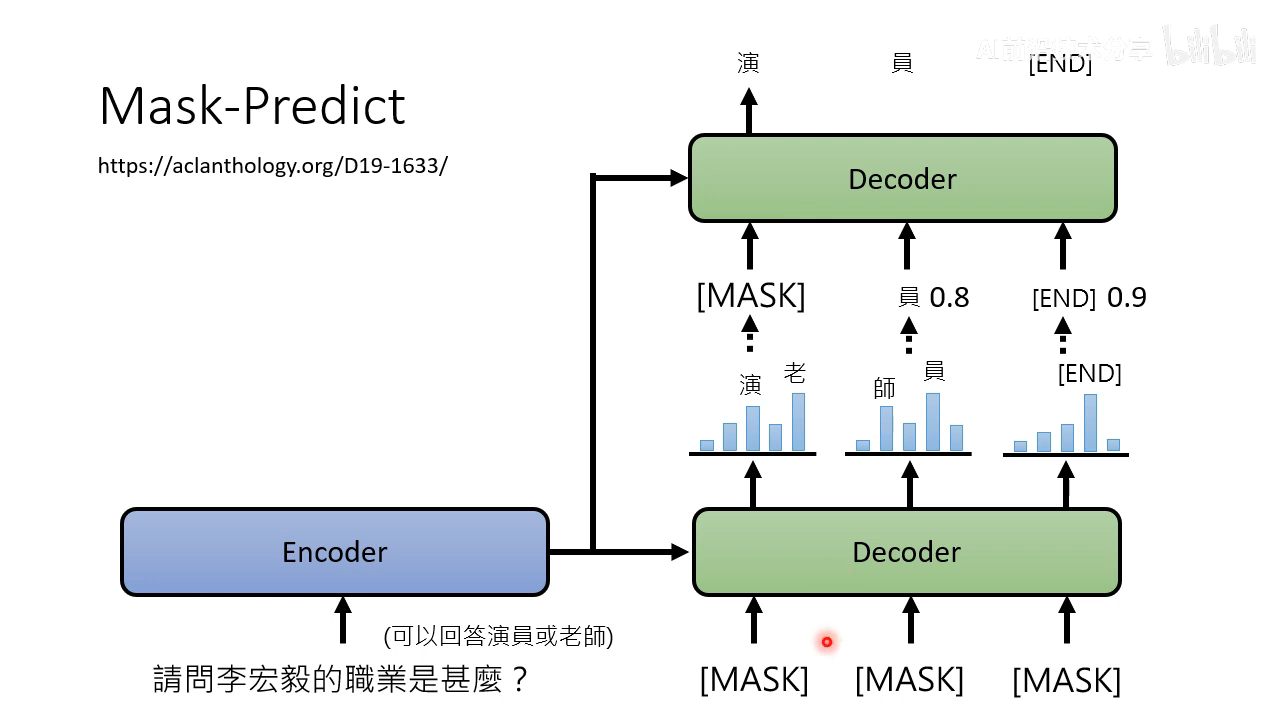
类似 MTP 的图像生成方式 MaskGIT，一般 mask 然后迭代预测 12 次效果就很好了

这种方式比 autoregressive 的迭代步数会少一些。

总结

本文为 Diffusion Model 课程的学习笔记，详细讲解了扩散模型（Diffusion Model）的基本原理、应用场景、以及与其他生成模型如 VAE 和 GAN 的对比。扩散模型主要用于生成高质量图像、音频和文本等数据，其核心机制包括前向扩散（逐步增加数据的噪声）和反向扩散（逐步去除噪声以恢复原始数据）。本文还介绍了扩散模型在图像生成中的多种应用，例如 Stable Diffusion 和 DALL-E 2。

此外，文章还深入探讨了扩散模型的数学原理，解释了如何通过最大似然估计和 KL 散度来训练模型，以及在生成过程中为什么需要添加噪声。文中提及的不同的扩散模型方法包括 latent diffusion 和 text-to-image 模型，说明了这些模型如何在隐空间进行操作以优化生成质量。

最后，讨论了扩散模型成功的原因，指出其实质上是一种 autoregressive model，通过多次迭代改进生成的数据质量。文章还分析了扩散模型在特定应用中的表现，如语音合成和文本生成，展示了其广泛的适用性和潜力。