行列式和矩阵相关

目录

行列式

通用方法

简单方法

余子式和代数余子式

矩阵

乘法

伴随矩阵

矩阵的逆

低阶行列式

初等矩阵的转置

初等矩阵的逆

左行右列  求逆矩阵

秩的结论

---

行列式

通用方法

自上而下化零 

使用代数余子式

简单方法

行列式 么型行列式 按照横展开 

爪型行列式 使用c 化零

余子式和代数余子式

eg

 余子式是除去剩下的元素构成的行列式

代数余子式是

矩阵

初等矩阵是指由单位矩阵经过一次初等变换得到的矩阵 

乘法

是M行M列

乘法公式 A的行依次乘以B的列

塌缩矩阵 主对角线是零 上面/下面有元素 相乘后向角落压 适用于A^n

伴随矩阵

若A是可逆的，则

其中二阶伴随矩阵等于 主对调 副相反数

矩阵的逆

低阶行列式

A的逆矩阵 = A的行列式分之一 *乘以A的伴随矩阵（适用于低阶行列式）

所有的伴随矩阵都有AA*=|A|E，若A还是可逆的 则A*=|A|A的逆

初等矩阵的转置

初等矩阵的逆

矩阵的行列式不为零 矩阵可逆 

E12（K）将第2行乘以K倍加到1上;E12 就是吧12行（列）互换;E1（K）就是把第1行都乘上K

AP = Pλ 求φ（A）等于P*φ（λ）P^-1

（AB）的逆等于B的逆乘以A的逆

其中倍乘-1/3的逆是-3  加减的逆是减加-2的逆是2 

可逆矩阵相当于若干个初等矩阵的乘积，代表了若干次初等变换

左行右列  求逆矩阵.

左行右列说的 求得矩阵位置

若AX=B 则可以使用 (A,B) 求得X 

中 在右边 对B进行 列变 P放上面 B放下面 之后将P位置换为E得到B

B  在左边进行行变 P在左边 将 P换成E 得到B

秩的结论

①0≤R(Amn)≤min{m,n}.r(A)≤m,r(A)≤n

②R(A^T)=R(A).

③若A~B,则R(A)=R(B)

④若P、Q可逆,则R(PAQ)=R(A)    （PAQ）=B ~A 把A 进行行变 列变得到B

⑤max{R(A),R(B)}≤R(A,B)≤R(A)+R(B)，

⑥R(A+B)≤R(A)+R(B）

⑦R(AB)≤minR(A)+R(B)，特别地:R(AA^T)=R(A^TA)=R(A) 

⑧若 AmnBnl:=O,则R(A)+R(B)≤n

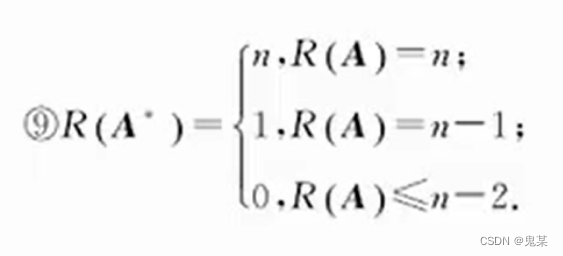
若R(Amn)=n,则R(AB)=R(B);若R(A )=m,则R(BA)=R(B)

证明⑧ 因为B（b1,b2,b3...bl）则A（b1,b2,b3...bl）=（0,0,0...0）Abi=0（i∈range（1，l+1））

若n阶矩阵是满秩 则肯定是可逆矩阵.

可逆矩阵乘以别的矩阵不改变别的矩阵的秩

可逆矩阵的的行列式是等于0

行列式不等于零 矩阵满秩

行*列 等于向量的内积

线性方程组

n元线性方程组Ax=b

(i)无解的充分必要条件是R（A）<R(A,b);

(ii)有唯一解的充分必要条件是R（A）=R(A,b)=n;

(iii)有无限多解的充分必要条件是R/(A)=R(A,b)<n

例:设A为m×n的矩阵 b为非零常数列，且r(A)= m<n,分析下列方程组接的情况

（注：非零常数列的特点 1.恒定性:数列的所有项都相等。2.非零性数列中的每一项都不等于零。3.简单性：数列的性质非常简单 便于就按和分析）

m<n 则矩阵A是个长方形

（a）Ax= b                 r(A) = r(A,b) = m <n ,无穷多解 列为n

（b）A转置x = b        {1.r(A转置)<r(A转置，b)无解 2.r(A转置)=r(A转置,b)=m 唯一解} 因为m是咧所以无穷多解不存在

（c）AA转置x = b      r(AA转置)=r(AA转置，b) = m  唯一解 列为m

（d）A转置Ax =b       {1.r(A转置A)=m<r(A转置A,b)无解 2. r(A转置A)=m=r(A转置A,b)无穷多节}    列为n 不可能有唯一解

行列式不等于零 矩阵满秩 

行*列等于向量的内积

矩阵乘以矩阵的转置 得出一个对称矩阵 若B= A*At 则 Bij= bji且 b的特征值是非负的

特征值该矩阵减去λE 求出来的特征值

方程组的同解  

（1）把方程组1的解带入方程组2 对任意k恒成立；

（2）系数矩阵的秩相等

例如：

若Ax=0，则ATAx=0 所以Ax = 0的均是A转置Ax=0的解

若 ATAx = 0 所以xTATAx =0即(Ax)T(Ax)=0 行*列= 内积 所以Ax = 0所以ATAx=0的解均是Ax=0的解

综上Ax=0与ATAx=0同解 r(A)=r(ATA)

向量组等价

定义

设有两个向量组A：a1a2a3...及B：b1b2b3b4....若B组中每个向量都能由向量组A线性表示则称向量组B能由向量组A线性表示，若向量组A与向量组B能相互线性表示则称两个向量组等价

1.r(A,B)=r(A)  <=> B组可有A组表示

2.r(A,B)=r(B) <=> A组可由B组表示

3.r(A,B)=r(A)=r(B),则称两个向量组相互等价（要求较高）

            矩阵相等则只要求r(A)=r(B)  （要求较低）

4.AB矩阵等价 即等型 秩相等即可 （经过初等变换）

5.在AB向量个数一样的情况下 向量组等价可推出矩阵等价 
    矩阵等价是向量组等价的必要不充分条件

6. AB =C C的列可以由A的列表示  BA = C C的行可由A的行表示

注：r(A)=r( AT) 乘在左边看行乘在右边看列

例题

可逆矩阵

规定

逆矩阵相当于若干个初等矩阵的乘积

理解

PQ为可逆矩阵 则PA=B AB矩阵是等价的 对应的向量关系是P在A的左边看行可以表示为A =P^-1B

得出 AB可以相互表示

齐次线性方程组

例7

因为 （α1,α2,α3，）=A 所以r(A)=r(B)  3是因为B有三列

特征值和特征向量

矩阵是几阶的特征值就有几个

α1*A =A的行列式的值  α2= （1,2，-1）的转置

特征向量倍数不同不能组合 倍数相同可以组合

当λ12 = 0时候 对应的特征值向量为 k1α1+k2α2  k1k2不全为零

（注：K一个的时候不可以为零 k多个的时候不全为零）