这里写目录标题
皮尔逊相关系数:
概念
总体 ——所要考察对象的全部个体叫做总体.
我们总是希望得到总体数据的一些特征(例如均值方差等)
样本 ——从总体中所抽取的一部分个体叫做总体的一个样本.
计算这些抽取的样本的统计量来估计总体的统计量:
例如使用样本均值、样本标准差来估计总体的均值(平均水平)和总体的标准差(偏离程度)。
例子:我国10年进行一次的人口普查得到的数据就是总体数据。
大家自己在QQ群发问卷叫同学帮忙填写得到的数据就是样本数据




这里的相关系数只是用来衡量两个变量线性相关程度的指标;
也就是说,你必须先确认这两个变量是线性相关的,然后这个相关系数才能告诉你他俩相关程度如何。
总结:
(1)如果两个变量本身就是线性的关系,那么皮尔逊相关系数绝对值大的就是相关性强,小的就是相关性弱;
(2)在不确定两个变量是什么关系的情况下,即使算出皮尔逊相关系数,发现很大,也不能说明那两个变量线性相关,甚至不能说他们相关,我们一定要画出散点图来看才行。
事实上,比起相关系数的大小,我们往往更关注的是显著性。(假设检验)
描述性统计
在matlab 中描述性统计:

excel也可以进行描述性统计:

spss 处理:

计算皮尔逊相关系数
在计算皮尔逊相关系数之前,一定要做出散点图来看两组变量之间是否有线性关系,
这里使用Spss比较方便: 图形 - 旧对话框 - 散点图/点图 - 矩阵散点图
代码:
R = corrcoef(Test) % correlation coefficient
得到:


美化相关系数表

对皮尔逊相关系数进行假设检验




皮尔逊相关系数假设检验:
第一, 实验数据通常假设是成对的来自于正态分布的总体。因为我们在求皮尔逊相关性系数以后,通常还会用t检验之类的方法来进行皮尔逊相关性系数检验,而t检验是基于数据呈正态分布的假设的。
第二, 实验数据之间的差距不能太大。皮尔逊相关性系数受异常值的影响比较大。
第三: 每组样本之间是独立抽样的。构造t统计量时需要用到
假设检验
x~f(x) 概率密度函数
F(x)累计密度函数


步骤:
-
写出H0和H1
-
在H0成立的条件下,得到统计量Z~f(x)

-
计算验证值,>0.05,同意原假设,反之,不同意原假设
正态分布检验
两种方法:
Shapiro‐wilk夏皮洛‐威尔克检验,小数据
JB检验,>30,大数据
一 JB检验
[h,p] = jbtest(x,alpha)
当输出h等于1时,表示拒绝原假设;h等于0则代表不能拒绝原假设。
alpha就是显著性水平,一般取0.05,此时置信水平为0.95
x就是我们要检验的随机变量,注意这里的x只能是向量。 ,
一列一列分析
% 检验第一列数据是否为正态分布
[h,p] = jbtest(Test(:,1),0.05)
[h,p] = jbtest(Test(:,1),0.01)
% 用循环检验所有列的数据
n_c = size(Test,2); % number of column 数据的列数
H = zeros(1,6); % 初始化节省时间和消耗
P = zeros(1,6);
for i = 1:n_c
[h,p] = jbtest(Test(:,i),0.05);
H(i)=h;
P(i)=p;
end
disp(H)
disp(P)
二 Shapiro‐wilk夏皮洛‐威尔克检验

还有一种方法Q-Q图:
qqplot(Test(:,1))
斯皮尔曼相关系数的假设检验
- 概念
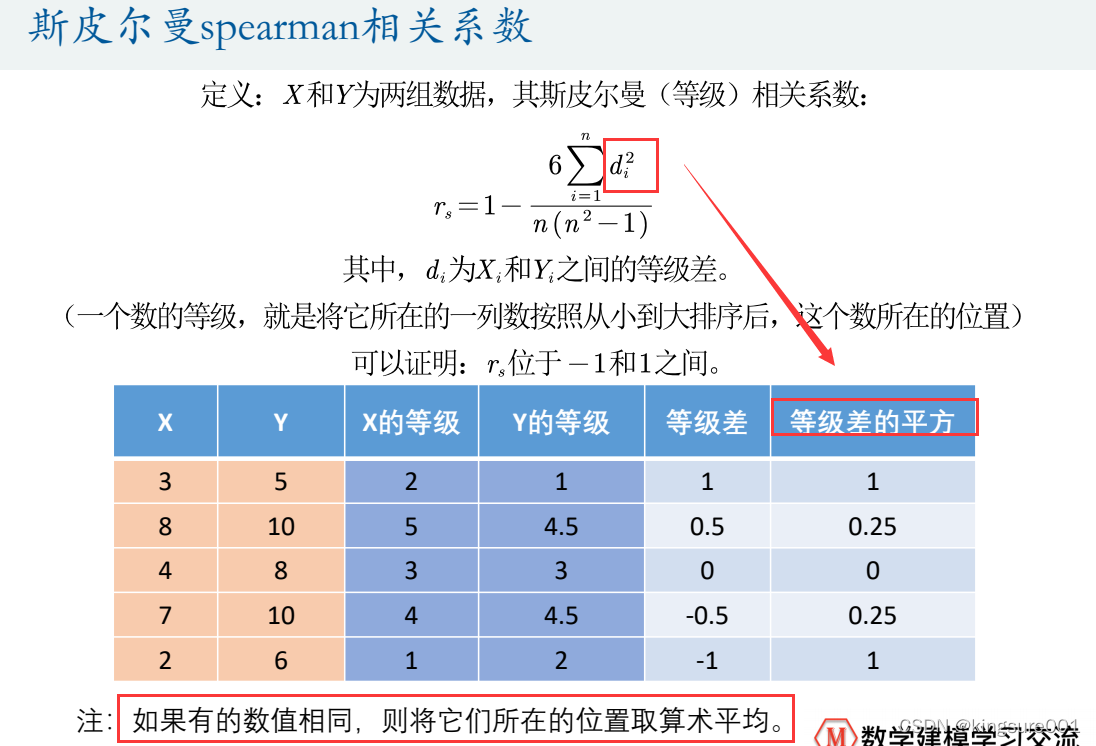
MATLAB中计算斯皮尔曼相关系数:
斯皮尔曼相关系数被定义成等级之间的皮尔逊相关系数。
[R,P]=corr(Test, 'type' , 'Spearman')
- 斯皮尔曼相关系数的假设检验:


整理,只用相关系数这一栏就可以
斯皮尔曼相关系数和皮尔逊相关系数选择:
大多用斯皮尔曼相关系数都可以
1.连续数据,正态分布,线性关系,用pearson相关系数是最恰当,当然用
spearman相关系数也可以, 就是效率没有pearson相关系数高。
2.两个定序数据之间也用spearman相关系数,不能用pearson相关系数。
定序数据是指仅仅反映观测对象等级、顺序关系的数据,是由定序尺度计量
形成的,表现为类别,可以进行排序,属于品质数据。
例如:优、良、差;
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








