怎么把数列和函数一一对应起来

怎么把数列和函数一一对应起来

通过幂级数进行对应

数列和变成函数——幂级数求和问题

在求幂级数的和函数时，先积后导法和先导后积法是两种不同的策略，它们可以用来简化求和过程。

先积后导法

想象你有一堆糖果，每堆糖果的数量都不同。你想要知道所有糖果的总数。先积后导法就像是你先将所有糖果堆成一列，然后数出总数。在数学中，这意味着你先对幂级数进行积分（将糖果堆成一列），然后对结果求导（数出总数）。

具体来说，如果你有一个幂级数 ( f(x) = \sum_{n=0}^{\infty} a_n x^n )，你想要找到它的和函数 ( F(x) )。你可以先对 ( f(x) ) 进行不定积分，得到 ( F(x) = \int f(x) , dx )。然后，对 ( F(x) ) 求导，得到 ( F’(x) = f(x) )。这样，你就找到了 ( f(x) ) 的和函数。

先导后积法

现在想象你有一堆糖果，每堆糖果的数量都不同。你想要知道所有糖果的总数。先导后积法就像是你先数出每堆糖果的数量，然后将这些数量加起来。在数学中，这意味着你先对幂级数求导（数出每堆糖果的数量），然后对结果进行不定积分（加起来得到总数）。

具体来说，如果你有一个幂级数 ( f(x) = \sum_{n=0}^{\infty} a_n x^n )，你想要找到它的和函数 ( F(x) )。你可以先对 ( f(x) ) 求导，得到 ( f’(x) = \sum_{n=1}^{\infty} n a_n x^{n-1} )。然后，对 ( f’(x) ) 进行不定积分，得到 ( F(x) = \int f’(x) , dx )。这样，你就找到了 ( f(x) ) 的和函数。

对比先积后导法和先导后积法在求幂级数和函数时的应用：

方法	描述	适用情况	步骤
先积后导法	先对幂级数进行积分，然后对结果求导	当幂级数的和函数难以直接求得时	1. 对幂级数 ( f(x) ) 进行不定积分，得到 ( F(x) = \int f(x) , dx )。 2. 对 ( F(x) ) 求导，得到 ( F’(x) = f(x) )。
先导后积法	先对幂级数求导，然后对结果进行不定积分	当幂级数的和函数难以直接求得时	1. 对幂级数 ( f(x) ) 求导，得到 ( f’(x) )。 2. 对 ( f’(x) ) 进行不定积分，得到 ( F(x) = \int f’(x) , dx )。

先积后导法

• 描述：这种方法适用于当你有一个幂级数，但直接求和函数比较困难时。通过先积分再求导，可以简化求和过程。
• 适用情况：当幂级数的和函数难以直接求得时，或者积分后求导比直接求和更简单时。
• 步骤：先对幂级数 ( f(x) ) 进行不定积分，得到 ( F(x) )，然后对 ( F(x) ) 求导得到 ( f(x) )。

先导后积法

• 描述：这种方法适用于当你有一个幂级数，但直接求和函数比较困难时。通过先求导再积分，可以简化求和过程。
• 适用情况：当幂级数的和函数难以直接求得时，或者求导后积分比直接求和更简单时。
• 步骤：先对幂级数 ( f(x) ) 求导得到 ( f’(x) )，然后对 ( f’(x) ) 进行不定积分得到 ( F(x) )。

这两种方法都是求幂级数和函数的技巧，选择哪一种方法取决于幂级数的具体形式和求解的便利性。在实际应用中，可能需要根据具体情况来选择最适合的方法。

函数变成数列——泰勒展开式问题

将函数展开为幂级数是微积分中的一个重要技巧，它允许我们用一个无穷级数来近似表示一个函数。这在数学分析、物理学、工程学等领域中非常有用。下面是一些将函数展开为幂级数的方法：

1. 泰勒级数展开

泰勒级数是将函数 ( f(x) ) 在某一点 ( a ) 展开为幂级数的标准方法。如果函数在 ( a ) 点可微，那么它的泰勒级数展开式为：

[ f(x) = f(a) + f’(a)(x-a) + \frac{f’‘(a)}{2!}(x-a)^2 + \frac{f’‘’(a)}{3!}(x-a)^3 + \cdots ]

其中 ( f’(a) )、( f’‘(a) )、( f’‘’(a) ) 分别表示函数在 ( a ) 点的一阶、二阶、三阶导数，依此类推。

2. 麦克劳林级数展开

麦克劳林级数是泰勒级数在 ( a = 0 ) 时的特殊情况。如果函数在 ( x = 0 ) 处可微，那么它的麦克劳林级数展开式为：

[ f(x) = f(0) + f’(0)x + \frac{f’‘(0)}{2!}x^2 + \frac{f’‘’(0)}{3!}x^3 + \cdots ]

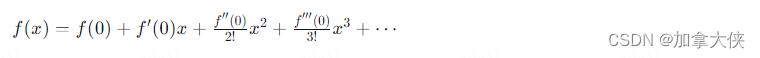
3.通过恒等变形，求导，积分等等转换成简单函数的幂级数展开，从而避免求高阶导

题外话

先积后导法和先导后积法

先积后导法

想象你有一块蛋糕，蛋糕上有一层糖霜。你想要知道蛋糕上糖霜的总量。先积后导法就像是先将蛋糕上的糖霜全部刮下来，然后称重。但是，如果你想知道的是糖霜在蛋糕上的分布情况，比如糖霜在蛋糕的哪一部分最厚，那么这个方法就不太适用了。

在数学中，先积后导法就像是先对一个复杂的函数进行积分（刮下糖霜），然后对结果求导（称重）。这个方法适用于当你需要知道整个函数的积分结果对某个变量的依赖程度时。

先导后积法

现在想象你有一块蛋糕，你想知道蛋糕的总重量。先导后积法就像是先称量蛋糕的重量，然后减去蛋糕上没有糖霜的部分的重量。这个方法适用于当你需要知道蛋糕上糖霜的重量时。

在数学中，先导后积法就像是先对一个函数求导（称量蛋糕），然后对结果进行积分（减去没有糖霜的部分）。这个方法适用于当你需要知道函数的某个部分对整个积分结果的贡献时。

应用

这两种方法在数学中非常有用，它们帮助我们解决各种问题。例如：

• 先积后导法：如果你想知道一个物体在不同时间的速度变化，你可以先计算物体的位移（积分），然后求导得到速度。
• 先导后积法：如果你想知道一个物体的总位移，你可以先求出物体的速度（求导），然后积分得到位移。

这两种方法就像是数学中的工具，帮助我们理解和计算函数的行为。选择哪种方法取决于你想要解决的问题类型。

在微积分中，先积后导法和先导后积法是两种不同的方法，用于处理复合函数的导数问题。这两种方法在解决某些特定类型的问题时非常有用。

先积后导法（Leibniz’s Rule）

先积后导法，也称为莱布尼茨法则，是一种用于求解复合函数导数的方法。它适用于求解形如 ( \int f(x, g(x)) , dx ) 的积分的导数，其中 ( f ) 是关于两个变量的函数，而 ( g(x) ) 是 ( x ) 的函数。

莱布尼茨法则的公式是：

[ \frac{d}{dx} \int_{a}^{g(x)} f(x, t) , dt = f(x, g(x)) \cdot g’(x) + \int_{a}^{g(x)} \frac{\partial}{\partial x} f(x, t) , dt ]

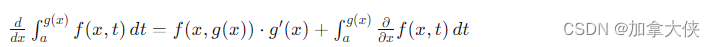
这个法则告诉我们，求解复合函数的导数时，可以先对内函数 ( g(x) ) 进行积分，然后对结果求导，同时还要加上一个积分项，该积分项是原函数 ( f(x, t) ) 关于 ( x ) 的偏导数在积分区间上的积分。

先导后积法

先导后积法，也称为分部积分法，是一种用于求解不定积分的方法。它适用于求解形如 ( \int u , dv ) 的积分，其中 ( u ) 和 ( dv ) 是 ( x ) 的函数。

分部积分法的公式是：

[ \int u , dv = uv - \int v , du ]

这个法则告诉我们，求解不定积分时，可以将积分分为两部分：一部分是 ( u ) 乘以 ( dv ) 的积分，另一部分是 ( v ) 乘以 ( du ) 的积分。通过这种方式，可以将复杂的积分问题转化为更简单的积分问题。