用复合函数求原本的函数两种方法
回溯法


等价变化法


代指法
数学上也允许自己定义变量,然后用定义的变量代指 明确存在的东西,然后应用于问题中。

- 2.


第一数学归纳法
验证条件 X1>a>0。
如果 Xn>a>0 能推出 Xn+1 > a > 0, 那么 Xn>a>0 成立。
解释:
“如果 Xn>a>0 能推出 Xn+1 > a > 0, 那么 Xn>a>0 成立。”
换句话说,不就是,如果前一个成立,那么后一也必然成立。
既然如此,那我们知道X1成立,那X2也必然成立,同理, 递推出Xn成立。
例题:
- 1.

- 2.

数列和的极限求法




一元函数性态问题
常见问题
求极值
通过第一充分条件、第二充分条件,不必多说。
求最值
将端点与所有导数为0的点进行比较即可。

答案:C, 注意讨论的驻点在不在区间内。
求离散函数最值

求单调区间
若不可以通过一阶导数判断,那么就结合二阶导数,通过凹凸性判断。
求凹凸区间
凹区间:二阶导数大于0的区间。
凸区间:二阶导数小于0的区间。
求拐点
第一充分条件,第二充分条件 ,不必多说。
求渐近线
铅垂渐近线、水平渐近线、斜渐近线,不必多说。
例题




求曲线交点个数

分析:
- 联立出方程。
- 通过高阶导数判断至多有多少根。
- 试点,然后运用零点定理。
- 答案:3
函数单调性关注要素
严格单调性

一阶导数大于等于0,当“=”成立时,有两种情况:1.变化的太平缓了,一阶导数测不出来(如 x3);2. x1 ≠ x2, f(x1) = f(x2)。
因此,我们实际上就是在证明是第一种情况,而不是第二种情况,因为,第一种情况导致的“=”成立不影响严格单调性。
点性质不能推区域

此题若无二阶导数存在条件,则B错误。
原因:函数在一点的导数值大于0,只能说明函数在这一点左邻域的点比它低,右邻域内的点比它高,并不能说明左右邻域内的高低性。
由于二阶导数存在,所以一阶导在该点连续,由极限保号性知,在该点邻域内一阶导大于0。
同理,可排除D。
函数在一点的二阶导数值大于0,只能说明函数在这一点处两边的点都在它上方(这里的“上面” 不是数值,是切线!),但具体怎么排列的,我们不知道。如果在该点二阶导数连续,由极限保号性,可对。
泰勒公式
牛顿插值法代替泰勒公式
引入

例题



近似函数:
通过这个近似函数可以看出,若要证的函数超过二阶可导,那么就不适合用牛顿插值法代替泰勒公式
因为,后面的操作非常复杂,不划算了…

总结
- 我们可以通过牛顿插值法生成一个逼近曲线的直线,然后再更具误差,添加多项式,使得直线弯曲,尽可能逼近曲线。
- 构造辅助函数F(x)=原函数 f(x) - 近似函数 g(x),由于我们的g(x)是f(x)的近似函数,因此,最靠前的几个F(x)函数值必为零,于是,我们便可引入罗尔定理进行讨论。
- 牛顿插值法代替泰勒公式产生更好效果,应满足情况以下情况:①函数导数最高阶<=2; ②可以确定两个点 “ ( x 1 , y 1 ) , ( x 2 , y 2 ) ”;
泰勒公式的应用
极限计算


在等价无穷小的应用

求高阶导数

带拉格朗日余项和佩亚诺余项的泰勒展开式




中值定理适用题型
| 探讨f 和 f’ | 用 拉格朗日中值定理 |
|---|---|
| 探讨f与f的高阶导数 | 泰勒公式 |
| 探讨 f, g 和 f’, g’ | 柯西中值定理 |
| 探讨 f’=0 | 罗尔定理、费马定理 |
| f=0 | 零点定理 |


延伸: 拉格朗日中值定理的重要作用之一:用 f’ 的大小来限定 f 的变化幅度大小



积分中值定理推广

反函数基本性质
关于y=x对称
值域和定义域互换


复合结果



反函数求导公式

导函数相对于原函数特有的性质
引入
- f(x) 在区间[a,b]上存在,函数值之间是无牵无挂的,连续存在还是间断存在都不一定。
- f(x) 在区间[a,b]上连续,函数值之间距离是一个无穷小量,点和点之间是有缝隙的。
- f(x) 在区间[a,b]上可导,函数值之间距离是一个比连续跟小的无穷小量,函数值之间的靠近速度非常快。
导函数性质
导函数极限与连续关系
如果导函数在一点处的极限存在,那么导函数在这个点必然是连续的。
分析: 如果一个函数在区间[a,b]上是可导的,则在该区间每个函数点的靠近速度必然非常快,距离非常近,那么 每个过函数点切线的斜率变化也几乎是连续的。 由此,我们可以推断出,导函数的函数值点也必然是非常接近的。
注意: 由于导函数可以含有震荡间断点,因此,导函数在一点存在,导函数在该点的极限不一定存在。

答案:C
A:在x=a处不一定可导。
B:导函数可以含有震荡间断点。
D:含有第一类间断点同样可以使导函数不存在。

介值性
如果函数f(x)在[a,b]上是可导的,且 在x=a处的右导数和 在x=b处的左导数 不等于0,那么 在(a,b)上存在u, 使f(u)=A, 其中A是介于 在x=a处的右导数和 在x=b处的左导数之间的任意值。
证明: 构造辅助函数+导数零点定理

保号性
如果在 [a,b] 上f’(x)≠0, 那么f’(x)恒正或恒负。
证明:
反证法,假设在 [a,b] 上f’(x)≠0,且f’(a)<0, f’(b)>0。
由导数零点定理知,存在u∈(a,b),使得f’(u)=0,
故,与原假设矛盾。
间断点
导函数必然不含第一类间断点和无穷间断点。
-
导函数不含第一类间断点,可以有导函数的几何意义分析知或者由导函数的介值性知。
-
导函数不含无穷间断点,理由:

-
是否含有震荡间断点是不确定的,因为震荡间断点不一定就是点与点离得不够近,只不过是不符合连续的定义罢了。

点连续或点可导推不出在其他地方也连续或可导
注意:f(x) 在 x=x0 处 (n+1)阶可导,可以推出 f(n) 在x0的一个邻域内可导。


答案:C
例题:



一元可微与二元可微
一元函数可微
是指过平面曲线上一点作切线,然后切点的邻域内的点与切线上的点之间的误差是一个高阶无穷小,即可替换,那么称该点可微。
其实,由可微的几何意义也可以知道,当满足一点可微时,那么该切点邻域内的点必然是充分靠近该点的,也就是该点左右两边的变化率必然相等,即该点可导。
另外,可以证出来,A=f’(x):

由以上可知,下图尖点处必然不可导也不可微。因为它没有一条统一的切线,并且随便一条切线都会使切点附近与切线的误差非常大。

于是,有定义:

二元函数可微
是指过空间曲面上一点作切平面,切点某方向的领域内的点(即每个方向上都必须满足)与切平面上的点之间的误差是高阶无穷小,即可替换,那么称该点可微。
从前面我们对一元函数可微的几何分析可以很容易理解二元函数可微的几何意义:
于是,有定义:
二元函数:
注意:以下的靠近程度一定要放到超实数领域内想象!!!
- 在x和y方向的偏导数存在,你只能说明曲面在这两个特殊方向的导数存在,并不能说明对应曲面上的点与切平面上的点是充分靠近的,因此,偏导存在并不能说明二元函数在该点可微。反过来,如果可微的话,那么该点周围的点必然是充分靠近的,因为要满足与切片面上的点的误差是高阶无穷小,故,周围方向上的导数也必然存在。
- 若二元函数在一点处的偏导存在且连续,那么在该点可微。理解: 该点处的偏导数是连续的,那也就是说,在这个点的周围的点在偏导存在要求靠近程度的基础上更加靠近,即可以达到可微的要求。
- 注意:三维曲面的一点在任何方向的导数存在,也不一定可微!待解释:(根据上面也能理解,导数存在,并不一定能满足该点周围的点与切片面上的点的误差是高阶无穷小)
- 可微的判别:(个人理解,其实不管是切点的哪一个方向上的增量对应的线性增量应该都是相同的,因为过该点的切平面应该符合唯一性,因为一但切面不唯一,曲面在该点几乎类似于一元函数里的尖点了,必然不可能可微,又因为是可微的(即切面上的点与切点周围的点充分靠近),所以线性增量才统一取成 dz=关于x的偏导 * △x + 关于y的偏导 * △y。 那么如果用 任意方向上的改变量-统一的线性增量…关系式符合可微定义的话,即可微)



总结
- 总的来说,不管是一元可微还是二元可微,都是要满足 全增量=线性增量+高阶无穷小
- 关系图

- 二元函数在一点可微,那么在该点的周围的点必然充分靠近切平面,即不可能出现间断点,故,多元函数在一点可微,那么在该点必连续。
一元函数积分
积分的精确定义

- 1.

数列和的极限求法




积分的简单物理应用

加速度就是速度的变化率
答案:B
反常积分的收敛性判别
一、如好积分,就用计算法直接判别。
二、不好积分,就用判别法(放缩、极限比值、p积分)。
步骤:
①拆分积分,一个积分符号带一个奇点。
②去掉无关因式。
③用等价无穷小或换元作恒等变形。


-
1.答案:B (由于lnx 趋向于正无穷或负无穷的速度非常慢,因此几乎不会对整体的收敛性产生任何影响。
)
-
2.



有理函数积分
如果n>=m, 那么一定可以化成多项式+有理函数形式。
如果积分形式是多项式之比,那么一定要向着有理函数积分的方向考虑。
- 如果积分函数不是有理函数,那就化成有理函数。
- 对分母的式子因式分解(需要的话)。
- 将整个有理函数拆分成若干个最简有理函数之和(拆分方法见下图),然后分别计算每一项的积分。

- Q式已经分解好的例题

- Q式未分解好的例题

- 已经是最简有理函数的例题

求分段函数的不定积分
选择题快速做法(根据原函数性质判断):
- 原函数必然连续,主要判断在分段点处是否连续。
- 对原函数在分段点两边分别求导,在分段点处单独求导,看是否等于导函数。
- 为什么要在分段点处单独求导?答:对一个函数整体求导,前提是这个函数在定义域内是可导的,在分段点处可能是间断的,所以要用定义特判。

分段函数求导:(原因已解释过)
- 非分段点处直接求
- 分段点处定义特判,求导。


参考答案:


变限积分性质

定积分比较
基本不等式解决

答案:B、C

数形结合

答案:A
基本法(作差+求导判断)
注意:如果直接作差求导麻烦,可以通过交叉相乘,做恒等变形。




二重积
注意陷阱!
1.如果遇到已经给你积分次序的形式,一定要注意它是否是合法的,即下限都必须小于等于上限!若不合法,那就颠倒一下,然后加负号。

由图知,若按y定限从0到2时,画直线,应该先交y=x,再交x=2,因此,上题显然不合法。

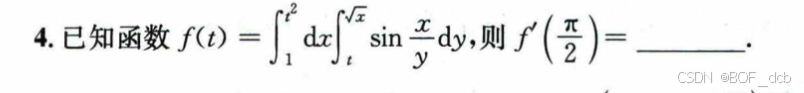
由于这题求的是在t=π/2处的变化率,因此,我们默认t的取指范围是 π/2的邻域,再这个基础上判断合不合法。

二重积分换元法
通用法
三换:函数+积分区域+…
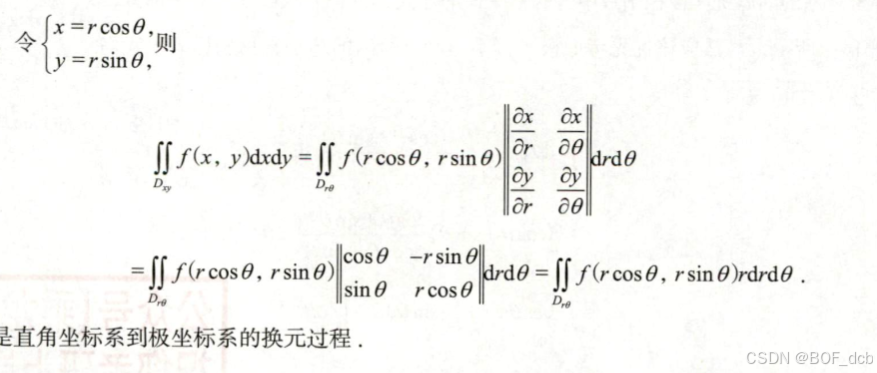
直角坐标系到极坐标系
同上。
积分区域为椭圆时合适的换元方法

例题:
注:把这题的最大值也求出来!

答案:D,最大值:4π/3 【仅供参考!】


隐函数存在定理


一个曲线在一个点的附近可以确定一个隐函数,那么前提这个点应在这个曲线上。
若在该点对应的偏导不得0,则可确定对应的隐函数。
答案:C
微分方程
1.二阶常系数齐次线性微分方程解的结构

2.二阶常系数非齐次线性微分方程解的结构

- 非齐次方程的通解 = 对应其次方程的通解 + 非齐次方程的特解。
- 将 非齐次方程的通解 里的常数C全都正常取值,就变成了 非齐次方程的特解。
例题

解释:
首先,它并不属于考纲要求的两种形式之一。
于是,由二阶常系数非齐次线性微分方程解的结构的①知,答案为B

解释:
- 先求非齐次通解,然后常数取符合题意的值,变非齐次特解。
- 由非齐次解的结构知,y1 - y3 和 y2 - y3 均为 对应齐次方程的特解,又因为它俩线性无关,于是可以由 二阶常系数齐次线性微分方程解的结构 知,齐次的通解。
- 然后用 齐次的通解 + 非齐次的特解(y3) 得到 非齐次通解 (这时候有两个独立常数)。
- 最后,根据初始化条件,得到答案。


解释:
- 首先,我们通过对应齐次方程的特解,可以知道齐次方程的通解形式,然后由通解形式可以得出齐次方程对应的 特征根 的值,由特征根的值可以求出齐次方程的特征方程,进而求出齐次方程的形式。
- 完成上述步骤 我们得到 …=f(x),方程左边已经求出,右边未知,由于已知 y1 是非齐次的解,那么把 y1 代入方程,此方程一定恒成立,由此可以得到 f(x)。 但是计算量过大,下面介绍另一种方法求 f(x)(分析解的结构)。
- 分析y1,用新的特解求f(x)。

3.n(n>2)阶常系数齐次线性微分方程


例题


解释(1):
先写对应的特征方程,求出特征根,然后按照特征根,出现什么,就写对应的东西。
解释(2):


共轭复根反推方程
注意:约定 i2 = -1

例题



方程计算



多项式除法

无穷级数
无穷级数概念

也就是 实数部分+超实数部分。
由无穷级数的概念我们可以知道,判断一个级数是否收敛,主要看超实数部分是什么情况。
特殊的级数
- 等比级数

性质
-
1.

-
2.

-
3.

-
4.

-
5.

级数判别法

正向级数敛散判别法

-
1.单调有界数列必有极限。

-
2.比较判别法

-
3.比较判别法的极限形式

-
4.

-
5.


-
6.根值判别法


-
6.积分判别法

交错级数敛散性判别法
- 莱布尼茨判别法


已知一个幂级数的敛散性讨论另一个敛散性





将函数展开成幂级数
通过恒等变形,如“先导后积或先积后导”化成下面形式。




例题

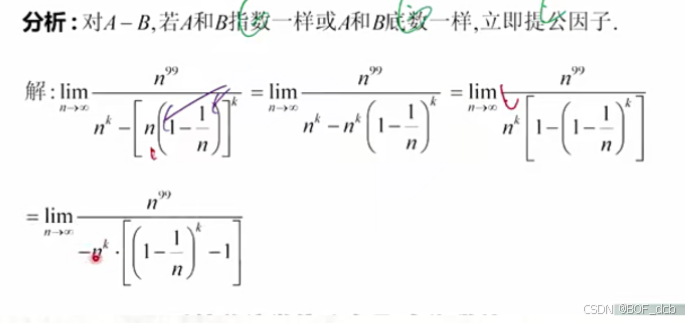
答案:100
判断级数敛散性:

解释:
思想同上,

解释:
当不能用加减拆项时,可以用奇偶拆项。



























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








