1. 算法思想
本文的算法思想,是放弃原有的基于支持窗口的方式,采用基于全局MST的方式,构建代价聚合公式。MST,采用像素之间颜色信息作为“边权值”,以全图的像素作为结点,构建过程中不断删除权值较大的边,然后用克鲁斯卡尔或者普里姆算法进行计算,求得最小生成树(MST),就得到了全图像素之间的关系。
因为支持窗口的办法,本质上只考虑了窗口内像素对中心像素的影响,窗口之外的像素的影响彻底忽略,其实想想看,这样做也没有什么不妥,但是它并不适用一些场合,比如文献列举的图像,
左上角的图像就是原始灰度图像,这个时候我们就会发现,这幅图像中像素与像素之间的关系用支持窗口来处理明显不灵,比如说周围框状区域的任何一个像素,肯定与框状区域内部的像素的深度信息一致,而与中间区域的像素不同。或者说,如果单考虑颜色信息,红框内的像素关系最大,如何表征这样的关系就是一个问题。很遗憾,我们不能事先提取出这样的区域,因为图像分割真的很耗时,并且不稳定,这就是作者的牛逼之处,他想到了MST可以表示这种像素关系,于是采用像素之间颜色信息作为“边权值”,进一步构建MST。
这里还要仔细说一下,这几幅图代表的其实是全图像素点对(0,0)点的权值大小,大家可以看一下论文里面BF的公式,也就是b、c两幅图,文章把参数看成了窗口的大小标志,如果参数足够大,其实exp里面的值就是0,空间信息的作用完全消失,这个时候就要看像素颜色差的作用了,我想这一点给作者一个提示,那就是BF中空间信息的考虑可能是多余的!!!于是作者只利用颜色差信息来构建MST。
MST指的是最小生成数,全称是最小权重生成树。它以全图的像素作为节点,构建过程中不断删除权值较大的边。注意,是全图所有的像素,然后采用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法进行计算。这样便得到了全图像素之间的关系。然后基于这层关系,构建代价聚合,这便是文章标题Non-Local Cost Aggregation的由来。
通过MST计算权值的效果如上图第二行所示,红色代表高权值,蓝色代表低权值。明显发现MST有效的表征了像素对像素的影响。代价聚合公式如下所示,具体的符号含义,这里就不说了,相信做过立体匹配的童鞋一眼就会看明白。
2. 算法核心
2.1 leaf-to-root
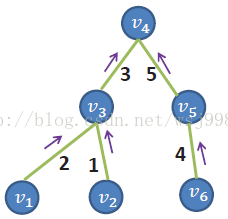
假设上图是一个MST,边上的数值代表权重,此时如果计算的是V4的代价聚合,那么很容易,直接计算子节点(V3, V4)的代价聚合值与各自边缘的乘积集合,因为V4是根节点,不需要考虑父节点的影响。公式如下所示,
箭头向上代表从叶子到当前节点的代价聚合值,为何只需要考虑子节点,而不考虑孙子节点,重孙子节点等等的原因就是由于在我们实际计算的时候,要从叶子节点一层一层往上算,这样就会利用树的特性,子节点的代价聚合值已经包含了孙子节点等等对我自己的影响。有点一本万利的感觉。。。
但是这样做是不够的,上面的V4没有父亲节点,属于特殊情况,如果我们要计算V3的代价聚合值呢?显然只考虑V1和V2是不够的,还得考虑V4的影响。也就是从上到下的影响。如图所示:
注意和上一幅图的区别,这个时候我们完全可以假设V3为根节点,它的父节点也变为他的子节点,这样的话,可以利用同样的办法,将V4的代价聚合值乘以它的权重一起再加进来。但是,这里还是有区别的,因为V4的代价聚合值已经考虑到了V3的影响,所以必须事先将V4的代价聚合值减去V3的代价聚合值才可以。公式如下所示:
其中,从上向下的代价聚合值就是最终的代价聚合值,同上一步一样的方式,要从上到下一层一层的计算代价,这样便可节省很多计算量。
2.3 时间复杂度
由于MST的性质,使得原本对全部像素的比较,只需要对父节点,子节点的比较即可,每次计算代价聚合值,从上述公式看来只需要一次加法,一次减法和三次乘法,这样便极大提高了速度,同时又考虑到了全局像素的影响。在middlebury上数据集的平均计算时间仅为90毫秒。
作者提供了文献和源代码的同时,也给出了一个ppt,就在作者的主页上,对其算法原理仍旧迷惑的童鞋可以下载去看看。
3. 实验效果&结论
实验效果就不介绍了,论文上一目了然,这篇文章提供了源码,大家可以跑跑看,我这边针对一般场景进行了测试,效果还是很不错的,经过进一步优化可以进行实际应用。这篇文章比较经典,一些后续的算法就是对其进行了改进,比如说分割树算法《Segment-Tree based Cost Aggregation for Stereo Matching》,将图事先进行区域分割,再在各个区域中计算MST,在生成MST的过程中,考虑到了颜色值与距离作为边缘权值,取得了比NL更好的效果。
附件:http://www.cs.cityu.edu.hk/~qiyang/publications/cvpr-12/
附上作者对于算法核心部分的PPT文档的下载地址,作者详细图解了算法的每一步,很详细。
上面的链接打不开可以在我的资源中下载:
作者关于核心算法做的PPT讲解:https://download.csdn.net/download/laobai1015/9657687









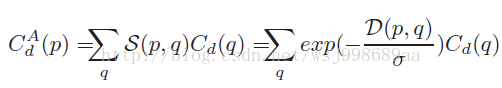















 889
889











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








