最大似然估计(MLE):
最大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。简单而言,假设我们要统计全国人口的身高,首先假设这个身高服从服从正态分布,但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的身高,但是可以通过采样,获取部分人的身高,然后通过最大似然估计来获取上述假设中的正态分布的均值与方差。
最大似然估计中采样需满足一个很重要的假设,就是所有的采样都是独立同分布的。下面我们具体描述一下最大似然估计:
首先,假设 为独立同分布的采样,θ为模型参数,f为我们所使用的模型,遵循我们上述的独立同分布假设。参数为θ的模型f产生上述采样可表示为
为独立同分布的采样,θ为模型参数,f为我们所使用的模型,遵循我们上述的独立同分布假设。参数为θ的模型f产生上述采样可表示为

回到上面的“模型已定,参数未知”的说法,此时,我们已知的为 ,未知为θ,故似然定义为:
,未知为θ,故似然定义为:

在实际应用中常用的是两边取对数,得到公式如下:

其中 称为对数似然,而
称为对数似然,而 称为平均对数似然。而我们平时所称的最大似然为最大的对数平均似然,即:
称为平均对数似然。而我们平时所称的最大似然为最大的对数平均似然,即:

原理:设X1, X2…Xn是取自总体X的一个样本,样本的联合密度(连续型)或联合概率密度(离散型)为f(X1, X2…Xn; Θ)。当给定样本X1, X2…Xn时,定义似然函数为L(Θ)= f(X1, X2…Xn; Θ)。
L(Θ)看作参数Θ的函数,极大似然估计使L(Θ)达到最大值的去估计真实值Θ。L()=,称为Θ的极大似然估计(MLE)。法就是用
最大似然估计中采样需满足一个很重要的假设,就是所有的采样都是独立同分布的。
基本思想:在已经得到试验结果(即样本)的情况下,估计满足这个样本分布的参数,将使这个样本出现的概率最大的那个参数Θ作为真参数Θ的估计。在样本固定的情况下,样本出现的概率与参数Θ之间的函数,称为似然函数。
一般步骤:
(1)由总体分布推导出样本的联合概率函数(或联合密度);
(2)将样本联合概率函数(或联合密度)中自变量看成一直常熟,把参数Θ看作自变量,得到似然函数L(Θ)。
(3)求似然函数L(Θ)的最大值点。
(4)计算过程中,为方便计算,常常先对似然函数取对数,再求导计算极大值点;若无法求导时,要用极大似然原则(即极大似然估计的定义:使L(Θ)最大)来求解。
最大后验概率(MAP):
最大后验估计是根据经验数据获得对难以观察的量的点估计。与最大似然估计类似,但是最大的不同时,最大后验估计的融入了要估计量的先验分布在其中。故最大后验估计可以看做规则化的最大似然估计。
首先,我们回顾上篇文章中的最大似然估计,假设x为独立同分布的采样,θ为模型参数,f为我们所使用的模型。那么最大似然估计可以表示为:

现在,假设θ的先验分布为g。通过贝叶斯理论,对于θ的后验分布如下式所示:

最后验分布的目标为:

最大后验估计是根据经验数据,获得对难以观察的量的点估计。与最大似然估计不同的是,最大后验估计融入了被估计量的先验分布,即模型参数本身的概率分布。
估计过程中,需利用先验概率和贝叶斯定理得到后验概率,目标函数为后验概率的似然函数,求得该似然函数最大时的参数值,即MAP的目标结果(利用极大思想)。
求解过程中,可用梯度下降等方法进行。
附:
贝叶斯估计
MLE、MAP和贝叶斯估计都是参数估计的方法,也就是需要预先知道或假设样本的分布形式,只是一些参数未知。
最大似然估计是最简单的形式,其假定参数虽然未知,但是为确定数值,就是找到使得样本的似然分布最大的参数。最大后验估计,和最大似然估计很相似,也是假定参数未知,但是为确定数值,只是目标函数为后验概率形式,多了一个先验概率项。
而贝叶斯估计和二者最大的不同在于,假定把待估计的参数看成是符合某种先验概率分布的随机变量,而不是确定数值。在样本分布上,计算参数所有可能的情况,并通过计算参数的期望,得到后验概率密度。
对样本进行观测的过程,就是把先验概率密度转化为后验概率密度,这样就利用样本的信息修正了对参数的初始估计值。在贝叶斯估计中,一个典型的效果就是,每得到新的观测样本,都使得后验概率密度函数变得更加尖锐,使其在待估参数的真实值附近形成最大的尖峰。
贝叶斯定理,是描述随机事件A和B的条件概率和边缘概率之间关系的定理。
其中,P(A|B)是指在B发生的情况下A发生的可能性。该公式是由P(A∩B)=P(A)*P(B|A)=P(B)*P(A|B)推导出来的。
P(A)是A的先验概率或边缘概率,之所以称为“先验”是因为它不考虑任何B方面的影响,表示在训练数据前假设A拥有的初试概率。
P(A|B)是已知B发生后A的条件概率,也由于得自B的取值,而被称作A的后验概率。
P(B|A)是已知A发生后B的条件概率,也由于得自A的取值,而被称作B的后验概率。
P(B)是B的先验概率或边缘概率,也作标准化常量(normalizing constant)。
在更一般化的情况,假设{Ai}是事件集合里的部分集合,对于任意的Ai,贝叶斯定理可用下式表示:
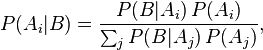








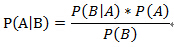
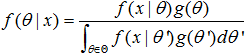














 54
54

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








