LeetCode435. Non-overlapping Intervals题解

1. 题目描述

Given a collection of intervals, find the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Note:

• You may assume the interval’s end point is always bigger than its start point.
• Intervals like [1,2] and [2,3] have borders “touching” but they don’t overlap each other.

【翻译过来】：给定了一系列区间interval，每个区间有一个首元素start和尾元素end，并且end > start，我们需要做这样的事情：在这一系列区间中，删除某些区间使得剩余的区间不存在重叠的情况，我们需要保证所删除的区间数目最少。此外类似[1, 2]和[2, 3]这样的边界接触的我们不认为是重叠。

2. 样例

Example1：

Input: [ [1,2], [2,3], [3,4], [1,3] ]
Output: 1
Explanation: [1,3] can be removed and the rest of intervals are non-overlapping.

Example2：

Input: [ [1,2], [1,2], [1,2] ]
Output: 2
Explanation: You need to remove two [1,2] to make the rest of intervals non-overlapping.

Example 3:

Input: [ [1,2], [2,3] ]
Output: 0
Explanation: You don't need to remove any of the intervals since they're already non-overlapping.

3. 分析

题目给出了一系列interval，这些interval也许不会按照顺序排列，题目的关键词提到了最小删除interval的数量，看到这个关键词，我很容易想到贪心算法。
因此，我设计的贪心算法目的是：在当前情况下，能保证当前已经访问过的interval的集合都是不重叠的，并且删除了最小数目的重叠interval。于是，我想到了两个思路，后来结果表明思路1是错误的。

3.1. 方法1：按照start升序排列

该算法的思想是：将所有的interval根据start元素升序排列，在start相同的时候，根据end升序排列。这样的序列我们进行这样的操作：从第二个interval开始，当后面的元素start小于前一个元素的end，说明就会发生重叠，就要将其删除，结果计数器counter记录一次，反之则代表不会重叠，以此类推，遍历一次后就会把重复的interval删去。

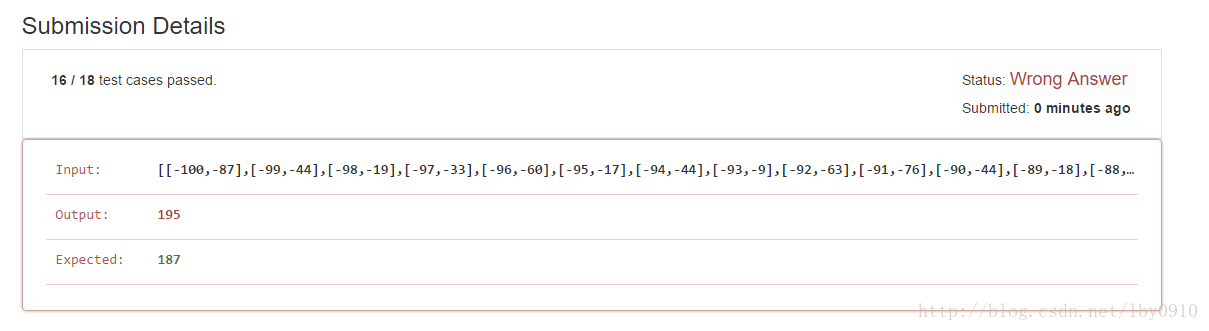
此法看起来有道理，但实际是错误的，因为考虑以下的情况：

Input: [ [1,2], [2,9], [3,4], [5,6] ]
/* We need only remove [2, 9] */
Right Output: 1 
/* Remove [3,4] and [5,6] */
Actually Ouput: 2 

3.2. 方法2：按照end升序排列

该算法的思想是：将所有的interval根据end元素升序排列，在end相同的时候，根据start升序排列。这样的序列保证了end从最小开始，我们只需判断每一个的interval的start是否会超过end即可，遍历算法与上一个方法类似。
这种算法的好处是：避免了因为end过大影响了其余interval的情况，即有些区间因为end过大了，甚至将很多start排在后面的区间包含了进去，这种情况下，我们应当删除这个end大的区间，才能保证最小删除区间的数目。

4. 源码

struct Interval {
    int start;
    int end;
    Interval() : start(0), end(0) {}
    Interval(int s, int e) : start(s), end(e) {}
};


static bool Compare(Interval a, Interval b) {
    if (a.end <= b.end) {
        if (a.end < b.end) {
            return true;
        }
        return a.start <= b.start;
    }
    return false;
}


int eraseOverlapIntervals(vector<Interval>& intervals) {
    int counter = 0;
    if (intervals.size() == 0) {
        return 0;
    }
    sort(intervals.begin(), intervals.end(), Compare);
    int reference = intervals[0].end;
    for (int i = 1; i < (int)intervals.size(); i++) {
        if (intervals[i].start < reference) {
            counter++;
        }
        else {
            reference = intervals[i].end;
        }
    }
    return counter;
}

5. 心得

贪心算法一旦找到了正确的每一步的处理目标和方法就会非常有效地节省时间和效率。这道题目的难度尾medium，它的难点应该就是在于如何对intervals进行处理，如果只是单纯地考虑start递增顺序遍历，删除元素，就会出现不能删除最小数目的interval情况。