Understanding Quaternions 中文翻译
原文地址:http://www.3dgep.com/understanding-quaternions/在计算机图形学中,我们使用转换矩阵来表示空间中的一个位置以及朝向。一个转换矩阵还可以表示对一个目标的缩放(scale)或错切(shear)等。 我们可以把转换矩阵想象成一个空间,当你用这个矩阵乘以向量、点(甚至矩阵)后, 你就把向量、点、矩阵转换进这个空间了。
在这篇文章中,我不会讨论转换矩阵的细节。你可以查看我前面的文章,文章中描述了转换矩阵的细节。
在这篇文章中,我想要讨论一个可替代的方案,即用四元数来描述空间里的物体的朝向。
四元数的概念是由爱尔兰数学家Sir William Rowan Hamilton发明的(1843年,都柏林)。Hamilton当时正和他的妻子前往爱尔兰皇家研究院,当他从Brougham桥通过皇家运河时,他领悟到了一个激动人心的东西,并立刻把它刻在桥的一个石头上:
1.复数
四元数可视为复数的扩展。在复数中,定义了,而四元数中则定义了
。然后如同复数定义出乘法,但复数的乘法是可交换的(commutative),而四元数的乘法是非可换的(non-commutative)。在复数平面中,可以用极坐标的几何方法理解乘法,但在四元数的四维空间中,就不是那么容易理解。
复数的其他知识可以自行百度,或者查看原文,我们只介绍计算机图形需要的相关知识。
我们能够把复数映射到一个2D网格平面——复数平面,只需要把实数映射到横轴、虚数映射到纵轴。
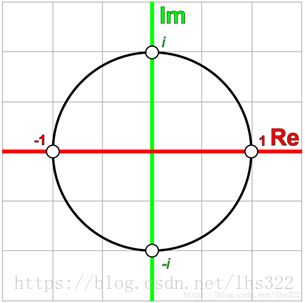
我们可以认为,对一个复数乘以i,这个复数就在复数平面上旋转了90度。
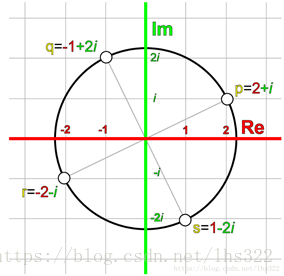
让我们看看这是不是真的。我们随机地在复数平面上取一个点:
p乘以i后得到q:
q乘以i后得到r:
r乘以i后得到s:
s乘以i后得到t:
t刚好是开始的p。如果我们把这些复数放到复数平面上,就得到下面的图:
我们也可以按顺时针方向旋转,只需要把上面的乘数i改成-i。
我们也可以在复数平面上进行任意角度的旋转,只需要定义下面这个复数:
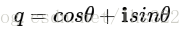
任意的复数乘以q:
也可以写成矩阵的形式:
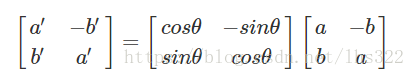
这也是一个在复数平面绕原点逆时针旋转任意点的方法。
了解了复数系统和复数平面后,我们可以额外增加2个虚数到我们的复数系统,从而把这些概念拓展到3维空间。
四元数的一般形式:
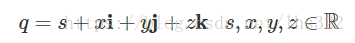
上面的公式是根据Hamilton的著名的表达式得到的:
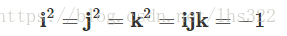
以及:
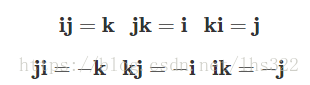
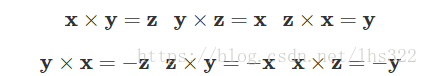
Hamilton自己也发现i、j、k虚数可以被用来表达3个笛卡尔坐标系单位向量i、j、k,并且仍然保持有虚数的性质,也即
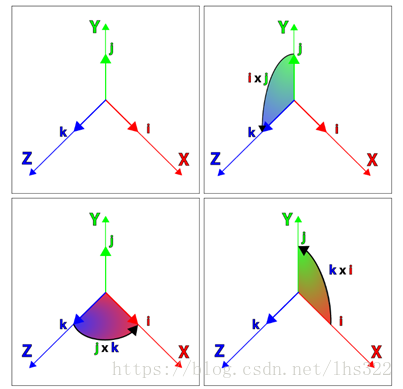
我们可以用有序对的形式,来表示四元数:
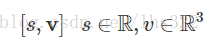
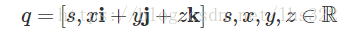
和复数类似,四元数也可以被加减:
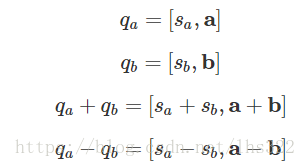
我们也可以表示四元数的乘积:
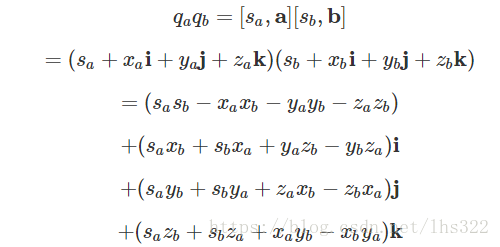
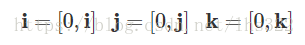
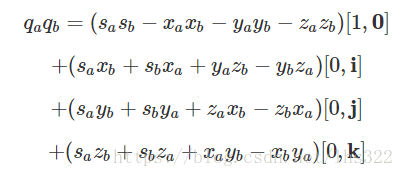
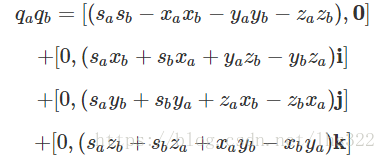
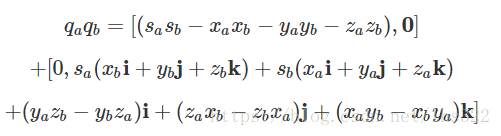
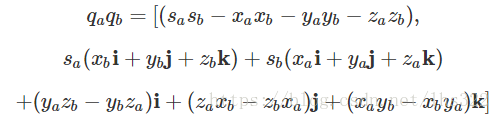
我们就得到了:
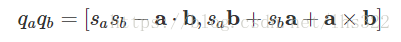
这就是四元数乘积的一般式。
回忆下复数范数的定义:
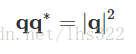
四元数的逆用q−1q−1表示。要计算四元数的逆,需要用四元数的共轭四元数去除以四元数的范数的平方:
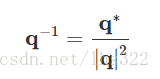
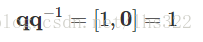
两边都左乘共轭四元数 q∗q∗ :
所以:
一个实四元数是一个虚部向量为零向量的四元数:
两个实四元数的乘积是另一个实四元数:
四元数的系数缩放
我们也可以用一个系数(实数)去乘四元数:
我们可以用实四元数与普通四元数的乘积,来确认这个等式是否正确:
和实四元数相似,Hamilton也定义了纯四元数。纯四元数是s=0的四元数:
也可以写成下面的形式:
然后是2个纯四元数的乘积:
我们可以把四元数写成实四元数和纯四元数的和:
给定任意的向量v,我们可以把这个向量写成一个系数和一个单位方向向量的乘积:
将这个定义和纯四元数的定义结合,就得到了:
然后,我们可以定义单位四元数了,它是一个s=0、vv为单位向量的四元数:
我们现在可以把单位四元数的定义和四元数的加法形式结合到一起,就创造了一种新的四元数的表示法,这种表示法和复数的表示法形似:
这就给了我们一种和复数非常相似的四元数表示法:
共轭四元数的计算,就是将四元数的虚向量取反:
四元数和它的共轭四元数的乘积:
四元数范数
类似的,四元数的范数可以这样定义:
这也让我们可以这样表达四元数范数:
利用四元数范数的定义,就可以对四元数进行规范化。要让一个四元数规范化,只需要让这个四元数去除以它的范数:
举一个例子,让我们规范化下面这个四元数:
第一步,先计算q的范数:
然后,q除以|q|:
和向量的点积相似,我们也可以计算2个四元数的点积,只需要将各个对应的系数相乘,然后相加:
我们也可以利用四元数点积,来计算四元数之间的角度差:
对于单位四元数,我们可以简化上面的等式:
前面我们定义了一个特殊的复数:旋转数。它是用来旋转2D复数平面的点的:
根据四元数和复数的相似性,应该有可能设计一个可以旋转3D空间的点的四元数:
让我们测试一下这个理论是否可靠,方法就是计算四元数q和向量p的积。第一步,我们把p写成纯四元数的形式:
以及单位四元数q:
从而:
我们可以看到结果是一个同时有系数、有虚向量的四元数。
让我们先考虑特殊的情形: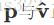
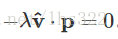
这时候,要使p绕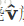
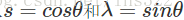
现在,让我们找一个例子来测试上面的公式。譬如绕z轴(就是k轴)旋转45度,那么我们的四元数q就变成:
然后,选一个特殊的p,并且p要和k轴正交,譬如把p放到i轴上,也就是:
好了,现在计算下qp:
这正是我们所期望的!
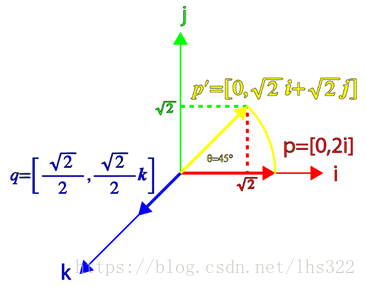
我们可以用图像展示旋转过程:
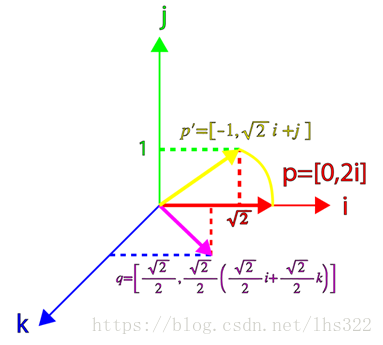
现在,让我们考虑更一般化的四元数,即和p不正交的四元数。现在让我们把p的向量部分偏移45度:
然后算qp:
代入我们设定的
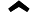

 v^,p,以及
v^,p,以及




θ=45∘,得到
注意,算出来的结果已经不是纯四元数了,并且,它并没有旋转45度、范数也不再是2(反而变小了,变为根号3)

我们可以用图像展示旋转过程:
然而),如果对qp右乘q的逆,出来的结果是一个纯四元数,并且四元数向量部分的范数可以保持不变。让我们试试应用在我们的例子里。
首先计算:
现在,把前面算出来的qp再次拿出来:
这下是纯四元数了,并且它的范数是:
这和原始的p的范数一致。
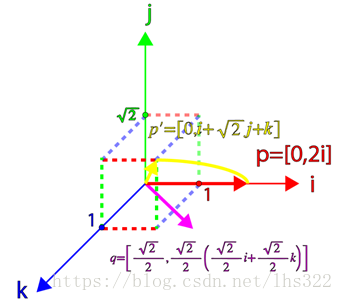
下面的图像展示了旋转结果:
所以我们可以看到,这个结果是一个纯四元数,并且原四元数的向量的范数也保持住了。但是还有一个问题:向量被旋转了90度而不是45度。这刚好是我们需要的度数的两倍!为了正确地让一个向量绕某个轴向量旋转某个角度,我们必须以目标角度的一半来计算。因此,我们构造了下面的四元数:
这就是旋转四元数的一般形式!
下一节中,我们将利用着一般形式,通过旋转轴的单位向量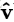









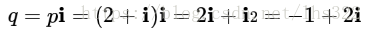
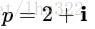
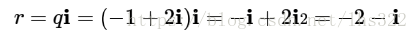
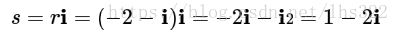
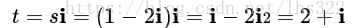
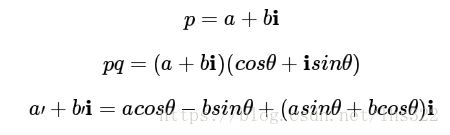
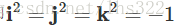
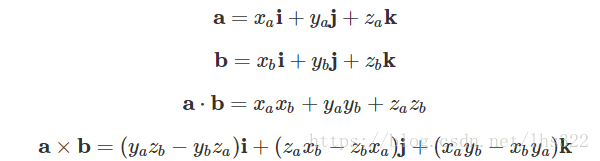
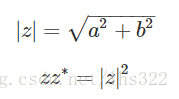
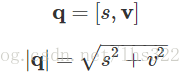
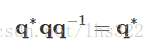
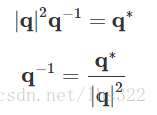
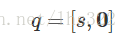
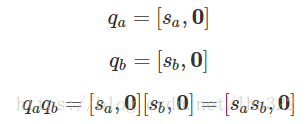
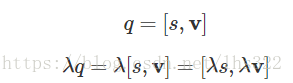
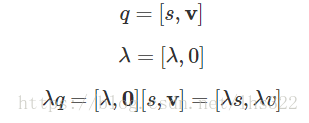
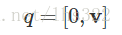
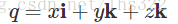
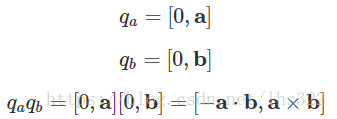
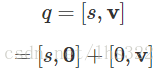
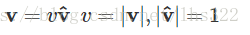
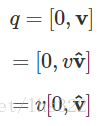
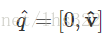
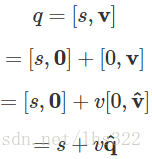
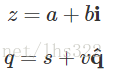
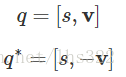
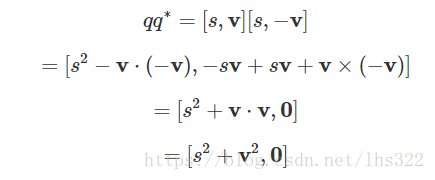
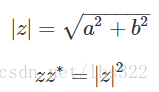
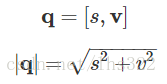
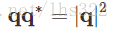
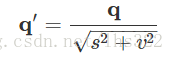
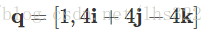
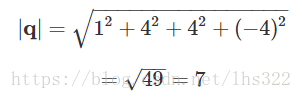
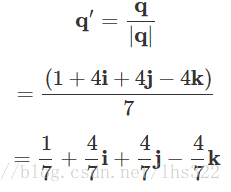
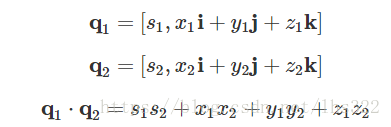
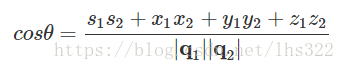
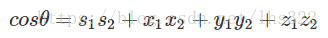
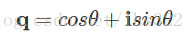
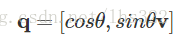
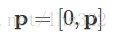
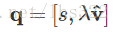
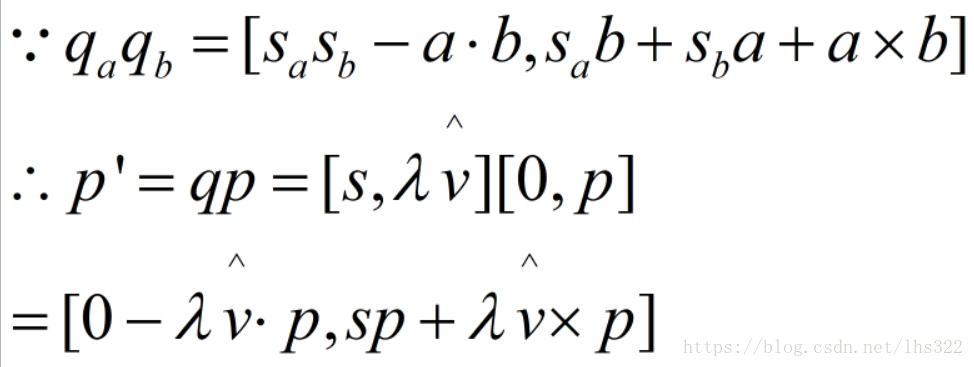
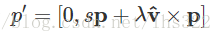
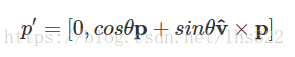
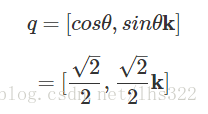
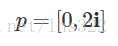
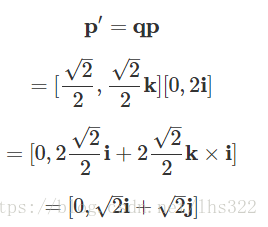
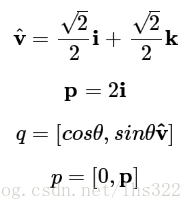
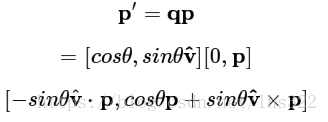
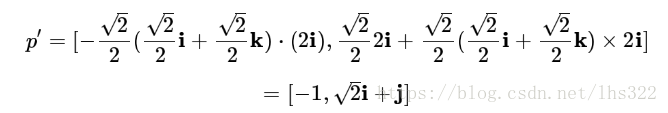
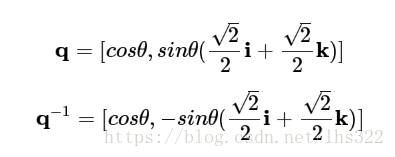
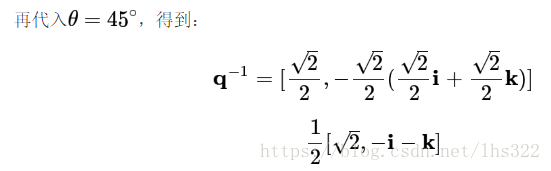
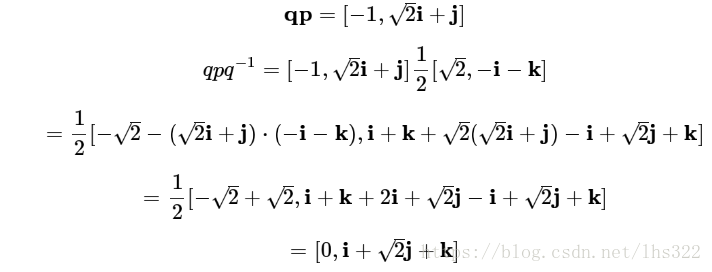
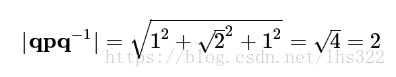
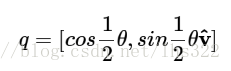














 799
799











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








