持续学习的综述: 理论、方法与应用（二：理论基础）

前文连接：持续学习的综述: 理论、方法与应用（一）

摘要

为了应对现实世界的动态，智能系统需要在其整个生命周期中增量地获取、更新、积累和利用知识。这种能力被称为持续学习，为人工智能系统自适应发展提供了基础。从一般意义上讲，持续学习明显受到灾难性遗忘的限制，在这种情况下，学习一项新任务通常会导致旧任务的表现急剧下降。除此之外，近年来出现了越来越多的进步，这些进步在很大程度上扩展了对持续学习的理解和应用。对这一方向日益增长和广泛的兴趣表明了它的现实意义和复杂性。在这项工作中，我们提出了一个全面的持续学习调查，寻求桥梁的基本设置，理论基础，代表性的方法，和实际应用。基于现有的理论和实证结果，我们总结了持续学习的一般目标，即在资源效率的背景下确保适当的稳定性-可塑性权衡和足够的任务内/任务间泛化性。然后，我们提供了一个最先进的和详细的分类，广泛分析了代表性方法如何解决持续学习问题，以及它们如何适应现实应用中的特定挑战。通过对有前途的方向的深入讨论，我们相信这种整体的视角可以极大地促进该领域乃至其他领域的后续探索。

题目：A Comprehensive Survey of Continual Learning: Theory, Method and Application
作者：Liyuan Wang, Xingxing Zhang, Hang Su, Jun Zhu, Fellow, IEEE
机构：Tsinghua University

3 理论基础

在本节中，我们总结了关于持续学习的理论努力，包括稳定性-可塑性权衡和概括性分析，并将它们与各种持续学习方法的动机联系起来。

3.1 Stability-Plasticity权衡

根据2.1节的基本公式，让我们考虑一个持续学习的一般设置，其中一个参数为θ的神经网络需要学习k个增量任务。假设每个任务的训练集和测试集遵循相同的分布Dt, t = 1，…， k，其中训练集 D t = { X t , Y t } = { ( X t , n , Y t , n ) } n = 1 N t D_t = \{X_t, Y_t\} = \{(X_{t,n}, Y_{t,n})\}_{n=1}^{N_t} Dt​={Xt​,Yt​}={(Xt,n​,Yt,n​)}n=1Nt​​包含Nt个数据标签对。目标是学习一个概率模型
(假设条件独立)，该模型可以很好地执行所有任务，表示为$D_{1:k}:=D_1，\dots ,D_k$。判别模型的任务相关性能可以表示为$logp(D_t|\theta )={\sum }_{n=1}^{N_t}log{p}_{\theta }(y_{t,n}|x_{t,n})$。持续学习的核心挑战通常来自于学习的顺序性:当从Dk学习第k个任务时，旧的训练集{D1，…、Dk−1}不可获取。因此，以一种平衡的方式捕捉新旧任务的分布至关重要，但却很困难，即确保适当的稳定性-可塑性权衡，过度的学习可塑性或记忆稳定性可能在很大程度上相互妥协(见图2,a, b)。

一个简单的想法是通过存储一些旧的训练样本或训练生成模型来近似和恢复旧的数据分布，这在第4.2节中被称为基于重播的方法。根据监督学习的学习理论[154]，旧任务的性能可以通过重玩更多接近其分布的旧训练样本来提高，但会导致潜在的隐私问题和资源开销的线性增加。生成模型的使用也受到巨大的额外资源开销，以及它们自己灾难性的遗忘和表达能力的限制。

另一种选择是通过在贝叶斯框架中形成持续学习，在更新参数时传播旧数据分布。根据网络参数的先验p(θ)，观察到第k个任务后的后验可以用贝叶斯规则计算:

其中，第k-1个任务的后验$p(\theta |D_{1:k-1})$成为第k个任务的先验，从而使新的后验$p(\theta |D_{1:k})$可以仅用当前训练集Dk计算。然而，由于后验通常是难以处理的(除了非常特殊的情况)，一个常见的选择是用$q_{k-1}(\theta )\approx p(\theta |D_{1:k-1})$来近似它，同样地，对于$qk(\theta )\approx p(\theta |D_{1:k})$。下面，我们将介绍两种广泛使用的近似策略:

第一种是在线拉普拉斯近似，它将$p(\theta |D_{1:k-1})$近似为具有局部梯度信息的多元高斯函数[177]，[202]，[222]，[371]，[441]。具体来说，我们可以将$q_{k-1}(\theta )$参数化，并构造一个近似的高斯后验$q_{k-1}(\theta ):=q(\theta ;{\varphi }_{k-1})=N(\theta ;{\mu }_{k-1}，{\Lambda }_{k-1}^{-1})$，通过对$p(\theta |D_{1:k-1})$的模态${\mu }_{k-1}\in R^{|\theta |}$进行二阶泰勒展开，其中${\Lambda }_{k-1}$表示精度矩阵，而 ϕ k − 1 = { µ k − 1 ， Λ k − 1 } ϕ_{k−1} =\{µ_{k−1}，Λ_{k−1}\} ϕk−1​={µk−1​，Λk−1​}，同样地，对于$q(\theta ;{\varphi }_k)$，${\mu }_k$和${\Lambda }_k$。根据Eq.(8)，学习当前第k个任务的后验模式可计算为

从${\mu }_{k-1}和$Λ_{k−1}$递归更新。同时，$Λ_k$从$Λ_{k−1}$递归更新:

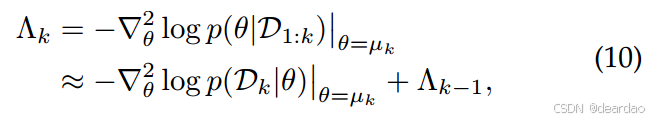
其中右边的第一项是Dk在µk处的负对数似然的Hessian，记为H(Dk，µk)。在实际应用中，由于$R^{|\theta |}$的维数很大，H(Dk，µk)的计算效率往往很低，并且不能保证近似的Λk对于高斯假设是正的半定。为了克服这些问题，通常用Fisher信息矩阵(FIM)来近似Hessian:

为了便于计算，FIM可以通过对角线近似[177]、[222]或kroneckerfactor近似[293]、[371]进一步简化。然后，通过保存旧模型的冻结副本${\mu }_{k-1}$来正则化参数变化来实现Eq.(9)，即第4.1节中基于正则化的方法。这里以EWC[222]为例，给出其损失函数:

其中，$l_k$表示任务特定的损失，FIM ${\hat{F}}_{1:k-1}={\sum }_{t=1}^{k-1}diag(F_t)$，每个Ft的对角近似diag(·)，λ是控制正则化强度的超参数。

二是在线变分推理(VI)[7]、[91]、[206]、[235]、[248]、[280]、[318]、[378]、[410]。有许多不同的方法可以做到这一点，有代表性的一种方法是在当前第k个任务上最小化满足$p(\theta |D_{1:k})\in Q$的族Q上的以下kl散度:

式中Zk为$q_{k-1}(\theta )p(D_k|\theta )$的归一化常数。在实践中，可以通过使用一个附加的蒙特卡罗近似来实现上述最小化进行逼近，满足$q_k(\theta ):=q(\theta ;{\varphi }_k)=N(\theta ;{\mu }_k,{\Lambda }_k^{-1})$作为多元高斯分布。这里我们以VCL[318]为例，哪个最小化了下面的目标(即最大化它的负数）：

其中KL-散度可以以封闭形式计算，并作为隐式正则化项。特别是，虽然Eq.(12)和Eq.(14)的损失函数形式相似，但前者是一组确定性参数θ的局部近似，而后者是通过从变分分布$q_k(\theta )$中抽样计算得到的。这归因于两种近似策略之间的根本差异[318]，[420]，在特定设置下的性能略有不同。

除了参数空间外，序列贝叶斯推理的思想也适用于函数空间[326]，[378]，[417]，它往往使参数更新更灵活。此外，VI还有许多其他扩展，例如用变分自回归高斯过程(VAR-GPs)改进后测更新[206]，构建任务特定参数[7]，[232]，[244]，[280]，以及适应非平稳数据流[235]。

本质上，对持续学习的约束，无论是重播还是正则化，最终都反映在梯度方向上。因此，最近的一些工作直接操纵了基于梯度的优化过程，在第4.3节中被归类为基于优化的方法。具体来说，当任务t的一些旧训练样本Mt保存在内存缓冲区中时，鼓励新训练样本的梯度方向与Mt的梯度方向保持接近[66]，[281]，[411]。它的表达式为$⟨{\nabla }_{\theta }{L}_k(\theta ;D_k),{\nabla }_{\theta }{L}_k(\theta ;M_t)⟩\ge 0$，对于t∈{1，…， k−1}，从而从本质上保证旧任务的损失不增加，即$L_k(\theta ;M_t)\le L_k({\theta }_{k-1};M_t)$，其中${\theta }_{k-1}$为学习第(k-1)个任务结束时的网络参数。

或者，也可以在不存储旧训练样本的情况下进行梯度投影[65]、[115]、[146]、[202]、[227]、[258]、[266]、[333]、[380]、[448]、[496]。这里我们以NCL[202]为例，它在在线拉普拉斯近似中使用${\mu }_{k-1}$和${\Lambda }_{k-1}$来操纵梯度方向。如Eq.(15)所示，NCL通过在以θ为中心的半径为r的区域内，以距离度量$d(\theta ，\theta +\delta )=\sqrt{{\delta }^T{\Lambda }_{k-1}\delta /2}$最小化任务特定的损失$l_k(\theta )$来进行持续学习，该区域通过精度矩阵${\Lambda }_{k-1}$考虑先验的曲率:

Eq.(15)中这类优化问题的解由$\delta \ast \propto {\Lambda }_{k-1}^{-1}\nabla \theta l_k(\theta )-(\theta -{\mu }_{k-1})$给出，由此得出学习率Λ的更新规则如下:

其中，第一项通过预条件${\Lambda }_{k-1}^{-1}$鼓励参数主要在不干扰旧任务的方向上变化，而第二项强制θ保持接近旧的任务解${\mu }_{k-1}$。

值得注意的是，上述分析主要是基于寻找所有增量任务的共享解决方案，这些增量任务会受到严重的任务间干扰[361]，[441]，[443]。相比之下，增量任务也可以以(部分)分离的方式学习，这是第4.5节中基于体系结构的方法的主要思想。这可以表示为构造一个参数为$\theta ={\cup }_{t=1}^k{\theta }^{(t)}$的连续学习模型，其中 θ ( t ) = { e ( t ) ， ψ } θ^{(t)} = \{e^{(t)}， ψ\} θ(t)={e(t)，ψ}， $e^{(t)}$是任务特定/自适应参数，ψ是任务共享参数。在某些情况下，任务共享参数ψ被省略，其中任务特定参数$e^{(i)}$和$e^{(j)}$ (i < j)可能重叠，以实现参数重用和知识传递。重叠部分$e^{(i)}$∩$e^{(j)}$在学习第j个任务时被冻结，以避免灾难性遗忘[379]，[384]。然后，如果给定任务标识$I_{D_t}$，则每个任务可以以$p(D_t|\theta (t))$而不是$p(D_t|\theta )$执行，其中任务之间的冲突被显式控制，如果省略ψ甚至可以避免:

然而，有两个主要的挑战。第一个是由于${\theta }^{(t)}$的逐步分配而导致的模型大小的可扩展性，这取决于$e^{(t)}$的稀疏性、$e^{(i)}$∩$e^{(j)}$(i < j)的可重用性和ψ的可转移性。二是任务同一性预测的准确度，记为$p(I_{D_t}=t|D_t，\theta )$。除了TIL设置总是提供任务标识$I_{D_t}$[108]、[117]、[379]、[384]外，其他场景一般都要求模型根据输入数据决定使用哪一个θ(t)，如式(17)所示。这与分布外(out- distribution, OOD)检测密切相关，其中分布内数据的预测不确定性应该较低，而分布外数据的预测不确定性应该较高[83]，[161]，[218]。更重要的是，由于任务同一性预测的功能如Eq.(18)(相当于任务分类)需要不断更新，它也遭受灾难性遗忘。为了解决这个问题，第i个任务的分布$p(D_t|i，\theta )$可以通过合并重播来恢复[139]，[161]，[223]，[244]:

式中边际任务分布在一般情况下$p(i)\propto N_i$。

持续学习的综述: 理论、方法与应用（三：泛化分析）

关注微信公众号，获取更多资讯内容：