微积分基础2-积分篇

目录：

三、积分

1、定积分概念

2、定积分的性质

1）基本性质   2）保序性   3）积分中值定理

3、微积分基本定理

1）原函数与变上限积分   2）牛顿-莱布尼茨公式★

4、不定积分

1）不定积分的概念与性质   2）积分表★   3）第一换元法(凑微分法)   4）第二换元法(变量代换法)

5）分部积分法   6）某几种函数的积分法   7）费曼积分★

5、定积分的计算

1）定积分的凑微分法   2）一个重要结论   3）定积分第二换元法   4）几个公式   5）分部积分法 

6）定积分近似计算★   7）举例

6、定积分的应用

1）微元法   2）几何应用-面积★

7、反常积分

1）无穷区间的反常积分   2）无界函数的反常积分

---

下续：微积分基础3-微分方程与向量

---

三、积分

∫形似一个拉长的S，即英文Sum求和的第一个字母，在几何中就是求取面积，积分的英文为integral。

1、定积分概念

或者假设0到1之间被平均分成了n份，那么每一份的宽度就是1/n。而矩形的高度就是函数的纵坐标的值，纵坐标可以通过y=x²很容易算出来。于是，第1个矩形的高度为（1/n）²，第2个为（2/n）²，第3个为（3/n）²……有了宽和高，把它们乘起来就是矩形的面积。于是，所有矩形的面积之和S就可以写成这样：

2、定积分的性质

1）基本性质

2）保序性

3）积分中值定理

3、微积分基本定理

1）原函数与变上限积分

函数f(x)在[a,b]区间上的定积分是一个常数(几何意义是曲边梯形的面积)，这个常数不含x，所以与积分变量的符号x无关(不管坐标横轴用什么记号，曲边梯形的面积一样)。

积分变量换作上限变量，再应用复合函数链式法则求导。

变限积分理解：

2）牛顿-莱布尼茨公式★

f(x)∈C[a,b]，f(x)变上限积分的导数就是被积函数，变上限积分是被积函数的一个原函数。

4、不定积分

1）不定积分的概念与性质

2）积分表★

积分是导数的逆运算。

3）第一换元法(凑微分法)

4）第二换元法(变量代换法)

主要有三角代换、根式代换和倒代换，适用积分式中有根式的。第二换元法是把被积函数里的积分变量x换成一个新的函数g(t)同时把dx也换成[g(t)]'dx。至于g(t)是怎么来的有一定的规律，但也不是绝对的。通常也是把被积函数里的某部分设成t，再反解出x = g(t)。

对于根号的积分常用第2换元法。

对于根号下有2次函数的情况下，通常写成完全平方和或平方差配方，然后做三角变换去根号。一个三角函数的平方减去一个常数是另外一个三角函数的平方。

根号外面有x的情况下，常常使用倒变换。

5）分部积分法

6）某几种函数的积分法

7）费曼积分★

此积分方法应用于信号与系统1-概述之一、概述之2、信号描述、分类与典型信号之3）几种典型信号之（4）抽样信号。

5、定积分的计算

1）定积分的凑微分法

2）一个重要结论

3）定积分第二换元法

4）几个公式

5）分部积分法

6）定积分近似计算★

从几何意义上考虑将曲边梯形分成 n个小曲边梯形（底边等长）。

（1）矩形法

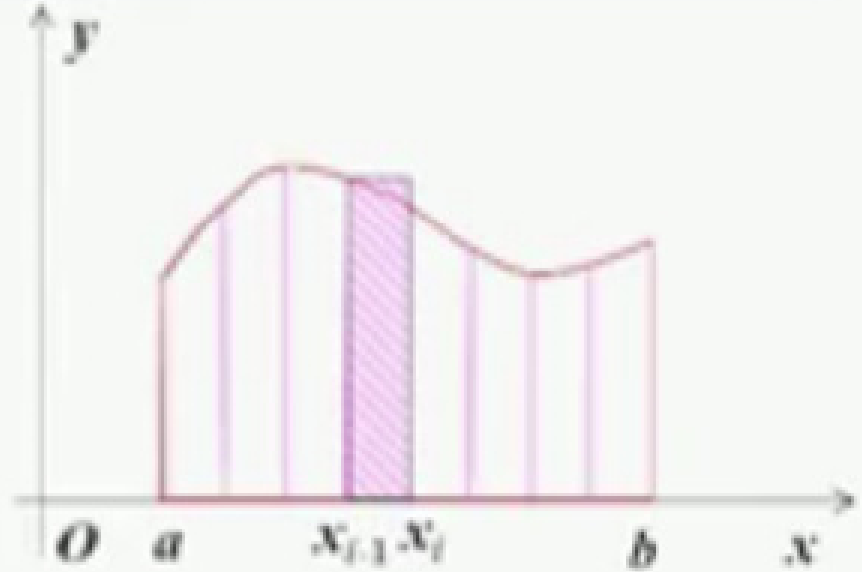
用矩形近似小曲边梯形则其面积近似

◆ 也可取右端边长为矩形高，得右矩形公式

◆ 误差为 1/n 的同阶无穷小

（2）梯形法

用梯形近似小曲边梯形，则其面积近似

上小曲边梯面积形近似为

导出近似公式

◆ 误差为的同阶无穷小

除了这种通过梯形法则计算(Excel画折线图做定积分)外，还有中段法则、Simpson法则、高斯积分、自适应积分法。

7）举例

6、定积分的应用

1）微元法

2）几何应用-面积★

7、反常积分

1）无穷区间的反常积分

2）无界函数的反常积分

---

无人扶我青云志，我自踏雪至山巅。觉得不错，动动发财的小手点个赞哦！