Critical Point ( local minima && saddle point)

CV小Rookie

于 2022-08-19 13:59:15 发布

阅读量1.2k

点赞数 3

分类专栏：边学边记文章标签：深度学习机器学习神经网络

本文链接：https://blog.csdn.net/like_jmo/article/details/126419655

版权

边学边记专栏收录该内容

28 篇文章

订阅专栏

当我们训练模型的时候，随著参数不断的 update，training 的 loss 不会再下降，但这时候的 loss 还没有到我们希望看到的样子，那很有可能是 deep network，没有发挥它完整的力量，所以 Optimization 显然是有问题的。

但是不管我们怎么 train 我们的模型，loss 迟迟不下降，就会猜想可能 loss 在下降的过程中遇到了微分为 0 的点，卡住了。每到这时，大家总会说这是 local minima 局部最小点，但是除了 local minima 以外，saddle point 鞍点也可能会造成微分为 0 。把梯度为 0 的点，我们统称 Critical Point 。

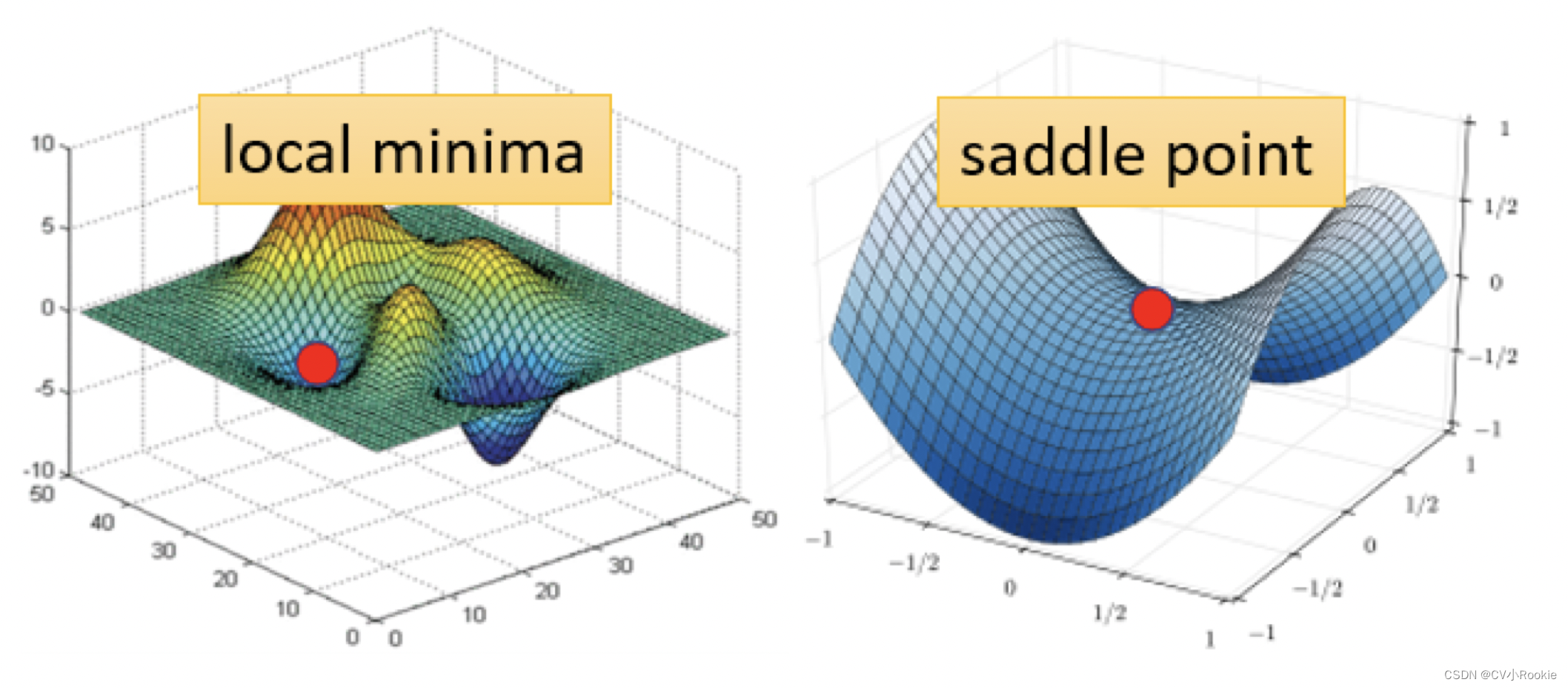
对于 local minima 和 saddle point 来说，虽然同样都是梯度为 0 ，但是：

因為如果是卡在local minima，那可能就没有路可以走了,因為四周都比较高,你现在所在的位置已经是 loss 最低的点，四周的 loss 都会比较高。
如果今天是卡在 saddle point 的话，saddle point 旁边还是有路可以让 loss 更低的。

所以鉴别今天我们走到 critical point 的时候，到底是 local minima 还是 saddle point 是一个值得去探讨的问题。

如果我们知道了 loss function 的形状，像上面那个图一样，我们就可以轻易看出是哪种类型。但是 deep learning 是非常复杂的，参数的维数是几百万甚至上亿，我们就没有办法画出 loss 的形状。

我们根据泰勒展开式，如果给定一个点 $\theta'$ ，那在 $\theta'$ 附近的函数是可以写出来的：

第一项 $L(\theta')$ 说明当 $\theta$ 与 $\theta'$ 比较接近时， $L(\theta)\sim L(\theta')$ 。
第二项 $(\theta - \theta')^{T}g$ ，用绿色的这个 g 来代表 gradient ，这个gradient会来弥补 $\theta$ 与 $\theta'$ 之间的差距。
第三项 $(\theta - \theta')^{T}H(\theta - \theta')$ 是弥补加上 gradient 后，和真实 $L(\theta)$ 的差距，H 是 Hessian矩阵。

如果我们今天走到的一个 critical point ，那么 gradient 为 0 ，第二项就消失了。所以我们可以通过判断 $(\theta - \theta')^{T}H(\theta - \theta')$ 来区分 local minima 还是 saddle point 。

其实《最优化》中也学过这个，通过判断 Hessian 矩阵正定 -> 极小值(local minima)；负定 -> 极大值；不定 -> 非极值点(saddle point)。

当然计算 H 的开销是非常昂贵的，这里我们只需要看其特征值，特征值全正就是 local minima；特征值全负就是 local maxima；特征值有正有负就是 saddle point 。

那 saddle point 不一样也会让训练停止，就算搞清楚是哪种 critical point 有什么意义？不用担心，其实 Hessian 矩阵暗指了 update 的方向。

这里 $u$ 代表 H 的特征向量， $\lambda$ 代表 $u$ 对应的特征值，就有： $u^{T}Hu=u^{T}(\lambda u)=\lambda \left \| u \right \|^{2}$ ，当 $\lambda$ 为负时，这一项整体为负。假如 $\theta -\theta' = u$ ，那么就会有 $L(\theta )<L(\theta')$ 。这样我们就可以说当遇到 saddle point 时，只需要沿着特征值为负的特征向量方向 update 就可以让 loss 降低。

那实际情况中 saddle point 多还是 local minima 多呢？先说结论，local minima 更少！举例：当处于一维空间中，或许处处是 local minima ，但是如果当参数变成两个，二维情况下或许原本的 local minima 就变成了 saddle point 。

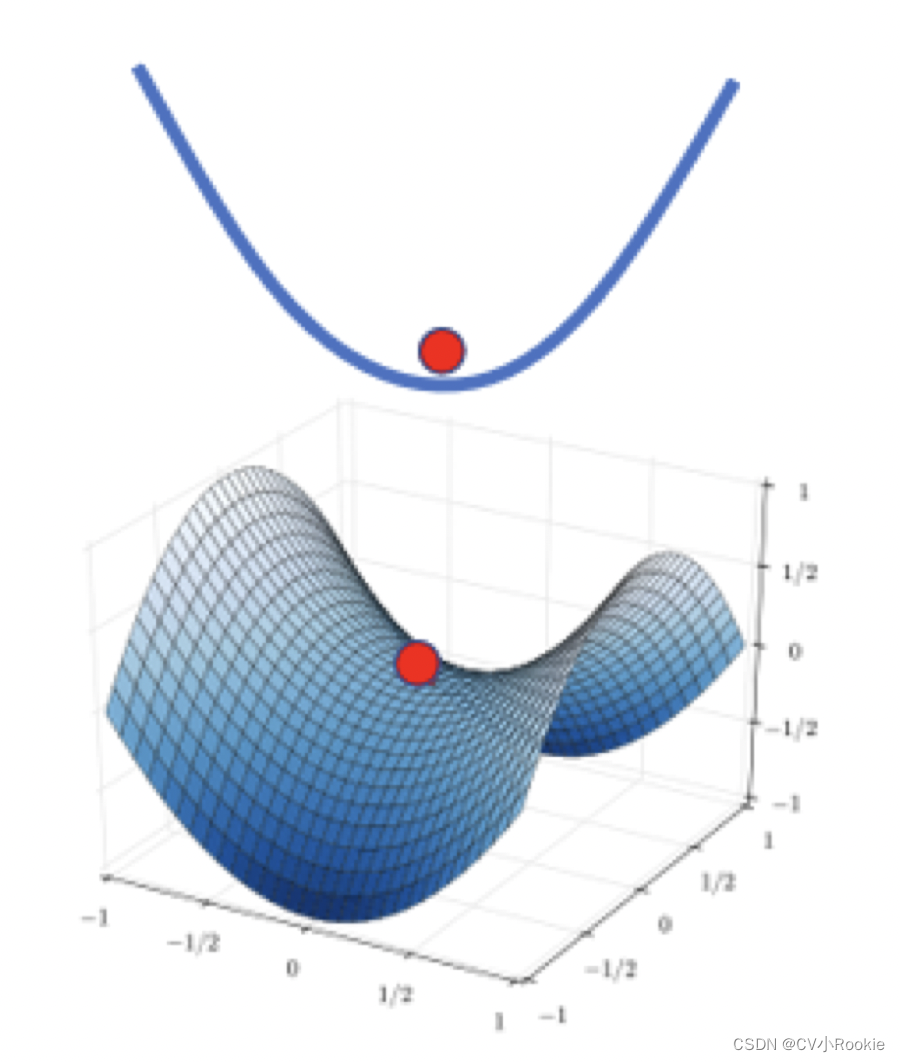
由于我们现在网络的参数都是百万千万级别的，所以 local minima 真的很少见！看图说话。

横轴的部分是 minimum ratio，是正的 eigen value 的数目和所有 eigen value 的数目之比。如果所有的 eigen value 都是正的，代表我们今天的 critical point 是 local minima 。如果有正有负代表 saddle point，那在实际上会发现说，几乎找不到完全所有 eigen value 都是正的 critical point。这个例子中 minimum ratio 最大也不过 0.5 到 0.6 间而已，代表说只有一半的 eigen value 是正的，还有一半的 eigen value 是负的。

所以从经验上看起来，其实 local minima 并没有那么常见。多数时候觉得 train 到一个地方 gradient 真的很小，然后所以参数不再update，往往是因为卡在了一个 saddle point 。