文章目录:
简单的二次曲面——【椭球面-柱面-正锥面-双曲面-抛物线-】154页
3.1 线性相关-线性无关定义线性无关-线性相关
6:等式-不等式【罗尔定理-拉格朗日中值定理-零点定理-夹逼定理】
各个章节
第一章:函数、极限与连续
基本函数:常、反、对、幂、指、三(常反对杨幂指我偶像唐三)
反三角函数图像
无穷小的比较
两个重要极限(或者说三个)
注意极限应用题
间断点的分类:第一类间断点,第二类间断点
函数的奇偶性
无穷小的替换
求反函数
=====================================================================================
第二章:一元函数微分学
导数的定义
导数微分的公式(特别是几个不好记的公式)
隐函数的导数与微分
曲线的凹凸性及其拐点最值极值
函数的单调区间和极值
经济函数
曲线的切线与法线
n阶导数公式
=====================================================================================
第三章“一元函数不定积分
不定积分的几个重要公式
不定积分的公式(特别是几个不好记的公式)
计算:
第一类:凑微分法
第二类:换元积分法
第三类:分布积分法法
反、对、幂、三、指【根据第一个u/v的向后顺序】
=====================================================================================
第四章:一元函数积分学
估值定理
积分中值定理
牛顿尼茨公式
定积分的奇偶性
广义积分【无穷-瑕积分】
旋转体的体积
积分求面积
一样的长*宽 = 底*函数
=====================================================================================
第五章:向量代数与空间解析几何
两点间距离
向量的模
方向余弦
数量积:a*b
向量夹角
向量积:a b c c=axb
向量的平行垂直
投影
空间平面的——一般方程,点法式方程,截距方程
空间直线的——一般方程,点向式方程,参数方程,两点式方程
两平面的位置关系
两直线的位置关系
点到平面的距离
直线到平面的位置关系
空间曲面及其方程——【球面-旋转曲面-锥面-柱面】
空间曲线——一般方程,参数方程,在坐标面上的投影
简单的二次曲面——【椭球面-柱面-正锥面-双曲面-抛物线-】154页
=====================================================================================
第六章:多元函数微积分学
高阶偏导数
全微分
复合函数的偏导数
空间曲线的切线与法平面——【切线方程-法平面方程】
空间曲面的切平面和法线——【切平面方程-法线方程】
二重积分的计算
交换积分次序
转换积分坐标形式
利用二重积分求面积,体积
曲线积分的计算
=====================================================================================
第七章:无穷级数
=====================================================================================
第八章:常微分方程
1.可分离变量的微分方程
2.齐次型方程
——准齐次型方程(238页)
3.一阶线性微分方程
——贝努利方程(241页)
——可降阶的高阶微分方程(245页)
4.二阶齐次线性微分方程
5.二阶非齐次线性微分方程
第九章:线性代数
1:行列式
1.1 几种特殊类型行列式(爪形......)
1.2 行列式性质
例如换行变号;各个行列相加提出一个数,乘法是乘某一行一列元素.......
1.3 降阶法(主对角线不能为0)
1.4 克莱姆法则
结果满足一一对应,非齐次线性方程组.......
1.5 行列式按照某一行列展开(n阶行列式)
1.6 行列式展开的拉普拉斯定理
2:矩阵
2.1 矩阵的四则运算
行乘列再相加(左边矩阵的列等于有右边矩阵的行)
2.2 矩阵的数乘
2.3 矩阵的转置
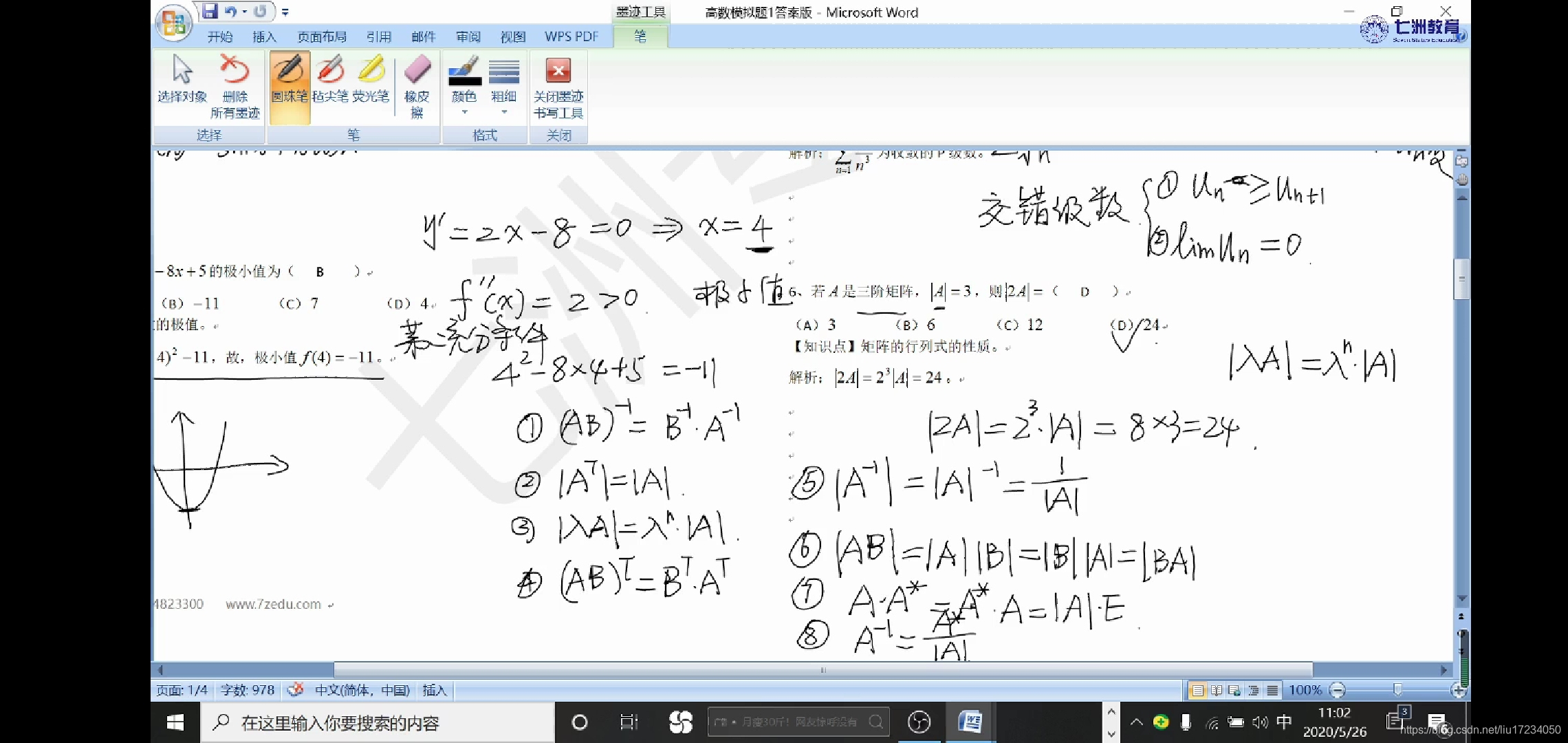
2.4 方阵的行列式
2.5 逆矩阵
2.6 分块矩阵
2.7 矩阵的初等变换
2.8 行阶梯型矩阵-行最简型矩阵-标准型矩阵
2.9 满秩
满秩,可逆
不是满秩,不可逆
3:向量组
3.1 线性相关-线性无关定义
3.2 线性相关-线性无关判别
4:线性方程组【线性无关-线性相关】
零解——线性无关——|A|不等于0
非零解——线性相关———|A|等于0
5:广义积分——无限积分;瑕积分


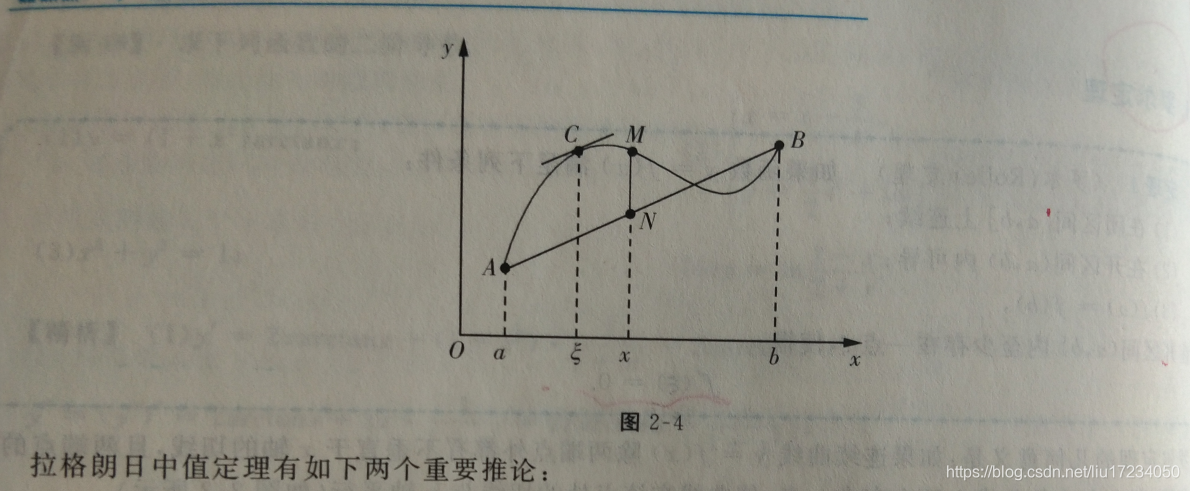
6:等式-不等式【罗尔定理-拉格朗日中值定理-零点定理-夹逼定理】
A: 罗尔定理-拉格朗日中值定理
B: 零点定理
C:夹逼定理
6.1 等式
7:参数方程确定函数的求导
8:曲线渐近线的求导【水平-垂直】
9:洛必达法则
0/0型:
分解因式
有理化
重要极限
等价替换
0因式
洛必达法则
10:多元函数的极值
10.1 二元函数的极值及其判定(无条件极值)
10.2 条件极值
11:利用极坐标计算二重积分

11.1 极点在区域的边界曲线之外
11.2 极点在区域的边界曲线之上
11.3 极点在区域的边界曲线之内部
12:对坐标的曲线积分的计算
13:格林公式

14:平面的曲线积分与路径无关的条件
15:幂级数的可微可导
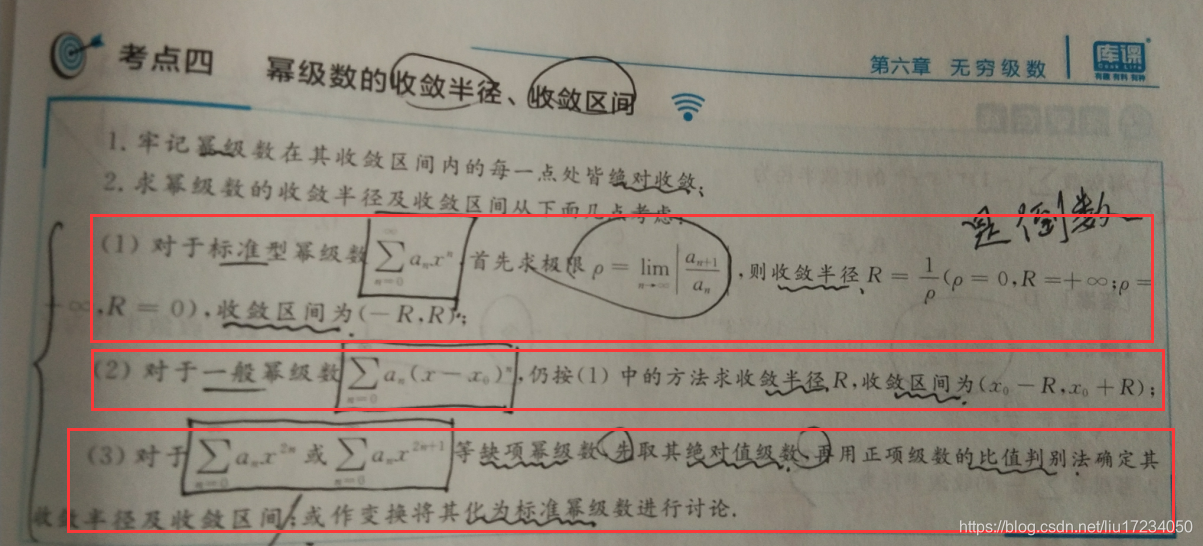
16.幂级数的收敛半径与收敛区间【缺项-不缺项】

17:函数展开成幂级数(泰勒级数-和函数)
17.1 泰勒级数
17.2 函数展开成幂级数
17.3 和函数
18:可降阶的高阶微分方程(3种类型)














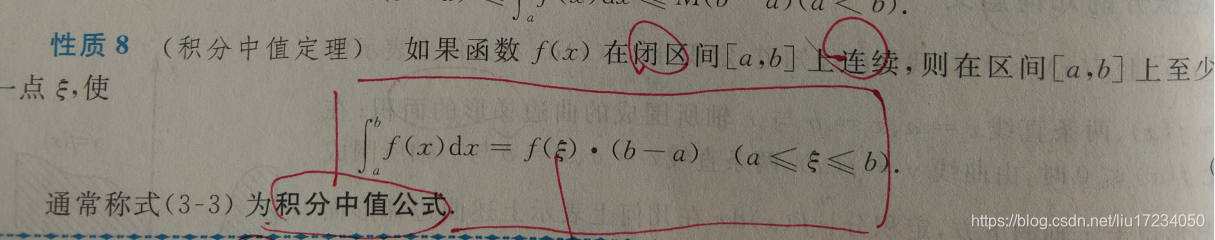
























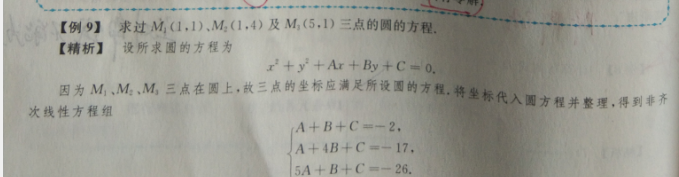






























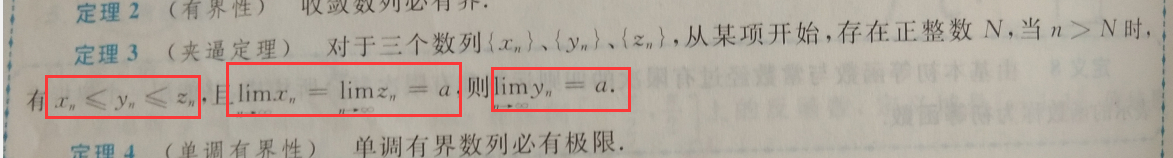















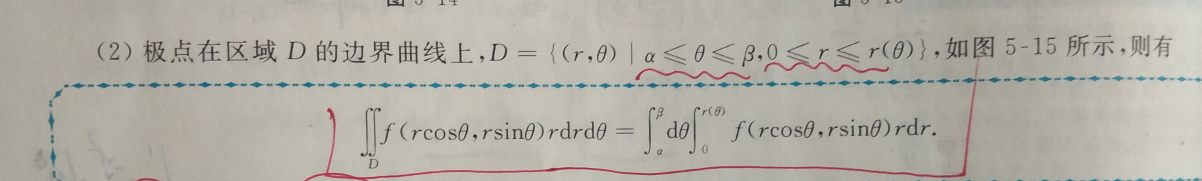






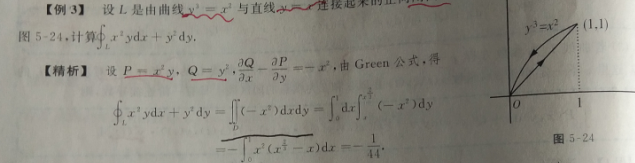










































 462
462

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










