Linux C语言程序设计(八)——树的基本概念介绍

1 定义及相关术语

1.1 树的定义

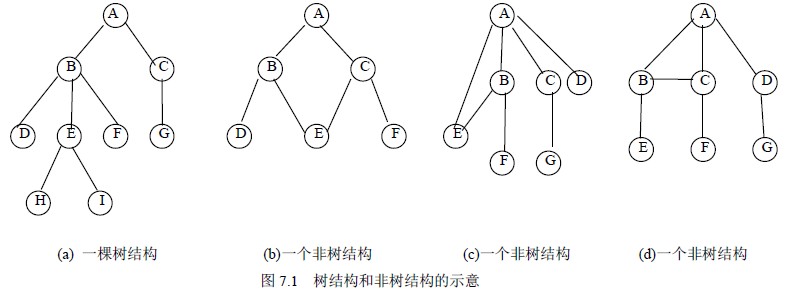
树（Tree）是n（n≥0）个有限数据元素的集合。当n＝0 时，称这棵树为空树。在一棵非树T 中：

（1）有一个特殊的数据元素称为树的根结点，根结点没有前驱结点。

（2）若n>1，除根结点之外的其余数据元素被分成m（m>0）个互不相交的集合T1，T2，…，Tm，其中每一个集合Ti（1≤i≤m）本身又是一棵树。树T1，T2，…，Tm 称为这个根结点的子树。

可以看出，在树的定义中用了递归概念，即用树来定义树。因此，树结构的算法类同于二叉树结构的算法，也可以使用递归方法。

1.2 相关术语

在二叉树中介绍的有关概念在树中仍然适用。除此之外，再介绍两个关于树的术语。

（1）有序树和无序树。如果一棵树中结点的各子树丛左到右是有次序的，即若交换了某结点各子树的相对位置，则构成不同的树，称这棵树为有序树；反之，则称为无序树

（2）森林。零棵或有限棵不相交的树的集合称为森林。自然界中树和森林是不同的概念，但在数据结构中，树和森林只有很小的差别。任何一棵树，删去根结点就变成了森林。

2、树的表示

树的表示方法有以下四种，各用于不同的目的。

1）直观表示法

树的直观表示法就是以倒着的分支树的形式表示，图7.1(a)就是一棵树的直观表示。其特点就是对树的逻辑结构的描述非常直观。是数据结构中最常用的树的描述方法。

2）嵌套集合表示法

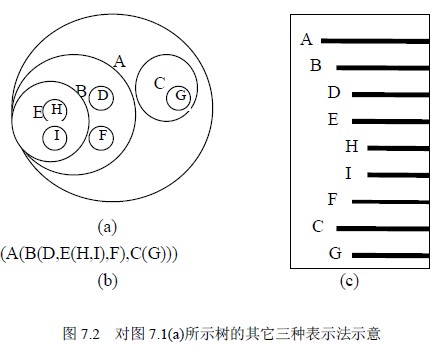
所谓嵌套集合是指一些集合的集体，对于其中任何两个集合，或者不相交，或者一个包含另一个。用嵌套集合的形式表示树，就是将根结点视为一个大的集合，其若干棵子树构成这个大集合中若干个互不相交的子集，如此嵌套下去，即构成一棵树的嵌套集合表示。图7.2 (a)就是一棵树的嵌套集合表示。

3）凹入表示法

树的凹入表示法如图7.2 (c)所示。树的凹入表示法主要用于树的屏幕和打印输出。

4）广义表表示法

树用广义表表示，就是将根作为由子树森林组成的表的名字写在表的左边，这样依次将书表示出来。图7.2 (b)就是一棵树的广义表表示。

2、 树的基本操作

树的基本操作通常有以下几种：

（1）Initiate（t）初始化一棵空树t。

（2）Root（x）求结点x 所在树的根结点。

（3）Parent（t，x）求树t 中结点x 的双亲结点。

（4）Child（t，x，i）求树t 中结点x 的第i 个孩子结点。

（5）RightSibling（t，x）求树t 中结点x 的第一个右边兄弟结点。

（6）Insert（t，x，i，s）把以s 为根结点的树插入到树t 中作为结点x 的第i 棵子树。

（7）Delete（t，x，i）在树t 中删除结点x 的第i 棵子树。

（8）Tranverse（t）是树的遍历操作，即按某种方式访问树t 中的每个结点，且使每个结点只被访问一次。

3、树的存储结构

        在计算机中，树的存储有多种方式，既可以采用顺序存储结构，也可以采用链式存储结构，但无论采用何种存储方式，都要求存储结构不但能存储各结点本身的数据信息，还要能唯一地反映树中各结点之间的逻辑关系。下面介绍几种基本的树的存储方式。

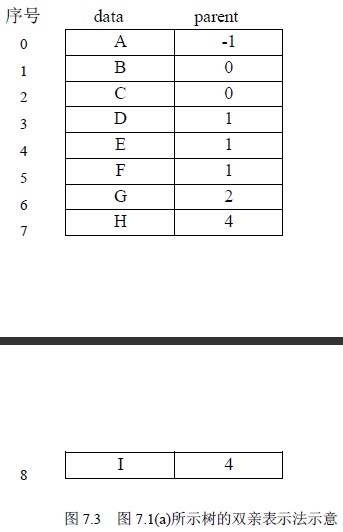
1）双亲表示法

2）孩子表示法

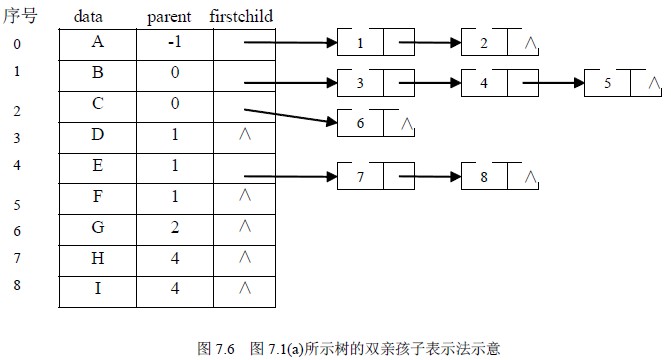
3）双亲孩子表示法

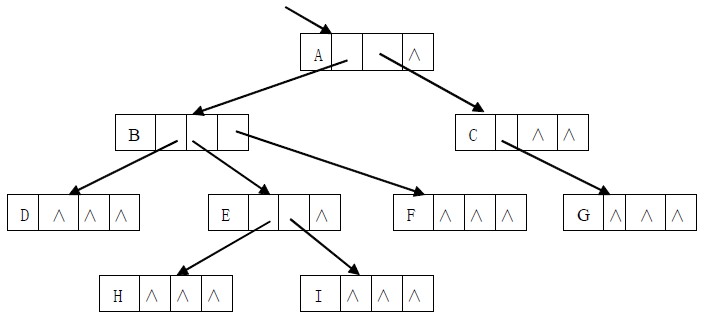
4）孩子兄弟表示法

4、树的遍历

树的遍历通常有以下两种方式。

4.1 先根遍历

先根遍历的定义为：

（1）访问根结点；

（2）按照从左到右的顺序先根遍历根结点的每一棵子树。

按照树的先根遍历的定义，对图7.8 所示的树进行先根遍历，得到的结果序列为：

A B E F C D G

4.2 后根遍历

后根遍历的定义为：

（1）按照从左到右的顺序后根遍历根结点的每一棵子树。

（2）访问根结点；

按照树的后根遍历的定义，对图7.8 所示的树进行后根遍历，得到的结果序列为：

E F B C G D A

根据树与二叉树的转换关系以及树和二叉树的遍历定义可以推知，树的先根遍历与其转换的相应二叉树的先序遍历的结果序列相同；树的后根遍历与其转换的相应二叉树的中序遍历的结果序列相同。因此树的遍历算法是可以采用相应二叉树的遍历算法来实现的。

5、判定树

在前面介绍了最优二叉树，即哈夫曼树在判定问题中的应用，在实际应用中，树也可用于判定问题的描述和解决，著名的八枚硬币问题就是其中一例。

设有八枚硬币，分别表示为a，b，c，d，e，f，g，h，其中有一枚且仅有一枚硬币是伪造的，假硬币的重量与真硬币的重量不同，可能轻，也可能重。现要求以天平为工具，用最少的比较次数挑选出假硬币，并同时确定这枚硬币的重量比其它真硬币是轻还是重。

问题的解决过程如图7.12 所示，解决过程中的一系列判断构成了树结构，我们称这样的树为判定树。

图中大写字母H 和L 分别表示假硬币较其它真硬币重或轻。下面对这一判定方法加以说明，并分析它的正确性。

从八枚硬币中任取六枚，假设是a，b，c，d，e 和f，在天平两端各放三枚进行比较。

假设a，b，c 三枚放在天平的一端，d，e，f 三枚放在天平的另一端，可能出现三种比较结果：

（1）a＋b＋c>d＋e＋f
（2）a＋b＋c＝d＋e＋f
（3）a＋b＋c<d＋e＋f

这里，只以第一种情况为例进行讨论。若a＋b＋c>d＋e＋f，根据题目的假设，可以肯定这六枚硬币中必有一枚为假币，同时也说明g，h 为真币。这时可将天平两端个去掉一枚硬币，假设它们是c 和f，同时将天平两端的硬币各换一枚，假设硬币b，d 作了互换，然后进行第二次比较，那么比较的结果同样可能有三种：

①a＋d>b＋e 这种情况表明天平两端去掉硬币c，f 且硬币b，d 互换后，天平两端的轻重关系保持不变，从而说明了假币必然是a，e 中的一个，这时我们只要用一枚真币（b，c，d，f，g，h）和a 或e 进行比较，就能找出假币。例如，用b 和a 进行比较，若a>b，则a 是较重的假币；若a＝b，则e 为较轻的假币；不可能出现a<b 的情况。

②a＋d＝b＋e 此时天平两端由不平衡变为平衡，表明假币一定在去掉的两枚硬币c，f 中，a，b，d，e，g，h 必定为真硬币，同样的方法，用一枚真币和c 或f 进行比较，例如，用a 和c 进行比较，若c>a，则c 是较重的假币；若a＝c，则f 为较轻的假币；不可能出现c<a 的情况.

③a＋d<b＋e 此时表明由于天平两端两枚硬币b，d 的对换，引起了两端轻重关系的改变，那么可以肯定b 或d 中有一枚是假硬币，再只要用一枚真币和b 或d 进行比较，就能找出假币。例如，用a 和b 进行比较，若a<b，则b 是较重的假币；若a＝b，则d 为较轻的假币；不可能出现a>b 的情况。

对于结果（2）和（3）的各种情况，可按照上述方法作类似的分析。图7.12 所示的判定树包括了所有可能发生的情况，八枚硬币中，每一枚硬币都可能是或轻或重的假币，因此共有16 种结果，反映在树中，则有16 个叶结点，从图中可看出，每种结果都需要经过三次比较才能得到。