由浅入深-全面学习和理解-偶极子天线（四）

上面已经讨论了无限小偶极子情况下的近远场的推导和计算，下面我们进一步讨论其这一特殊但非常经典的情况。为了更加全面的了解偶极子的特点和场强分布情况，我们分别从不同的场区表达式入手进行分析，看看每个场区的场强分别都有什么特点。

偶极子的一般示意图

首先，感应场即 kr≪1 的情况，其一般表达式为

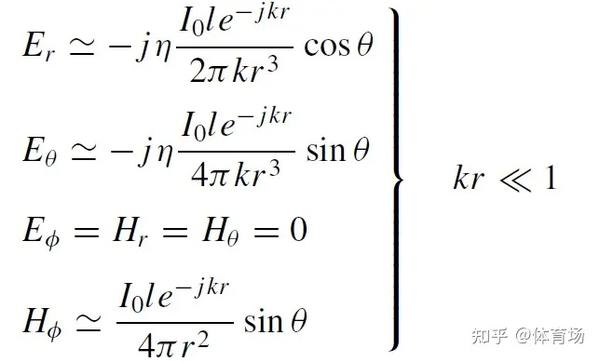
这是任意长度偶极子的一般远场表达式

按照偶极子的物理长度 l=λ/2 ，k=2πλ=ωμϵ ，则上述表达式由于kr≪1，则会有

Er=−jηI04(kr)2rcos(θ)

Eθ=−jηI08(kr)2rsin(θ)

Hϕ=I04kr2sin(θ)

在波长和电流分布取有限值的情况下，上述表达式的结果有

Er≫1

其最大值取在 θ=0 处，即为直角坐标系下的+z轴方向。

Eθ≫1

其最大值取在 θ=90 处，即为直角坐标系下的xy平面内。

Hϕ≫1

其最大值取在 θ=90 处，即为直角坐标系下的xy平面内。

在常规的 Eθ 外还多出来一个Er，这个Er是只有在近场才会有的分量而且由上面可以其数值应该会很大（近距离三次方反比），同时他的场强分布刚好与Eθ的取值角度范围和方向有一定的互补性，正常来说Eθ 和Hϕ共同形成一个面包圈，如之前所示，而Er则刚好与其互补（旋转90°，幅度缩放一倍）。

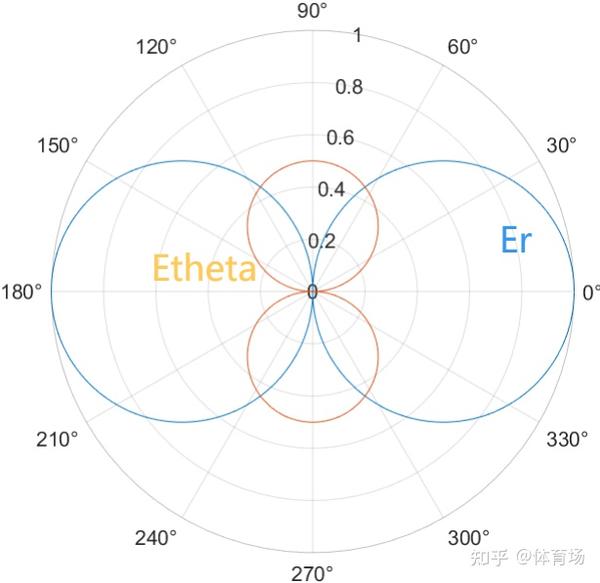
两组场强互补示意图

由上图可以看出，在感应近场区，Er的分量其实比Eθ幅度上要大一倍，说明在近场区域，Eθ分量并不占优势。反而是径向分量占绝对优势。实际上的偶极子是有尺寸的并非是理想点源，所以其近场的场强分布并非如上图那样曲线完美，但上图足以说明场强分量问题的核心特性。

下面研究一下能量传输，波印廷矢量

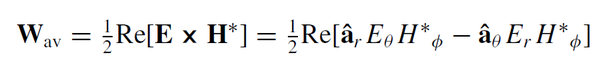
矢量叉乘

E→×H→∗=|a^ra^θa^ϕErEθEϕHr∗Hθ∗Hϕ∗|=|a^ra^θa^ϕErEθ000Hϕ∗|=EθHϕ∗a^r−ErHϕ∗a^θ

由于相乘之后两项都为虚数，所以

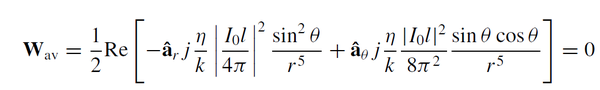
由于近场中的电场分量与磁场分量相差90°相位，从波印廷矢量的计算中可以发现，并没有能量流出，更多应该是储能。这也是为什么称之为凋落波的原因，某种程度上凋落波就是局域能量的存储，其并不满足传播的条件。

其次，感应场即 kr>1 的情况，其一般表达式为

任意长偶极子的近场表达式

按照偶极子的物理长度 l=λ/2 ，k=2πλ=ωμϵ ，则上述表达式由于kr>1，则会有

Er=ηI02ke−jkrr2cos(θ)

Eθ=jηI04e−jkrrsin(θ)

Hϕ=jI04e−jkrrsin(θ)

在波长和电流分布取有限值的情况下，上述表达式的结果有 Er 不可忽略 ，其最大值取在 θ=0 处，即为直角坐标系下的+z轴方向。

Eθ 不可忽略其最大值取在 θ=90 处，即为直角坐标系下的xy平面内。

Hϕ 不可忽略其最大值取在 θ=90 处，即为直角坐标系下的xy平面内。

虽然距离进一步拉远但这时Er仍然存在，这个Er现在相比感应场距离正在衰减，其随着距离的衰减速度也从距离的三次方变为二次方，它的场强分布仍然保持与Eθ的取值角度范围和方向的互补性，正常来说Eθ 和Hϕ共同形成一个面包圈，如之前所示，而Er的幅度正在减小。

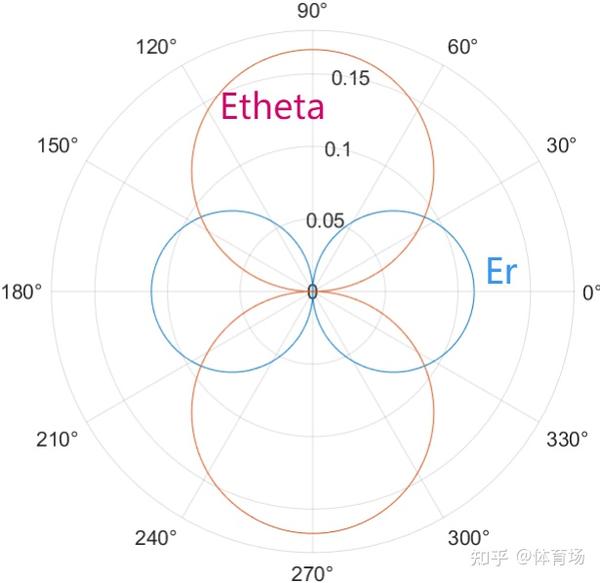
由上图可以看出，在近场区，Er的分量正在衰减，而Eθ分量比重不断提高。这说明从近场到远场的过程中，正是径向分量不断减小（虽然所有的电场分量都在随着距离而衰减）而切向分量不断占据主导的过程。

下面研究一下能量传输，波印廷矢量

Wav=12Re[E→×H→∗]=12|a^ra^θa^ϕErEθEϕHr∗Hθ∗Hϕ∗|=12|a^ra^θa^ϕErEθ000Hϕ∗|=12[EθHϕ∗a^r−ErHϕ∗a^θ]=12[η(I04)2e−j2krr2(sinθ)2a^r+jηI028ke−j2krr3cosθsinθa^θ]=12η(I04)2e−j2krr2(sinθ)2a^r

近场中的电场分量与磁场分量仍然存在90°相位差，但已经有可以传播的能量。

第三，感应场即 kr≫1 的情况，其一般表达式为

此时按照偶极子的物理长度 l=λ/2 ，k=2πλ=ωμϵ ，则上述表达式由于kr>1，则会有

Eθ=jηI04e−jkrrsin(θ)

Hϕ=jI04e−jkrrsin(θ)

从上式能发现，在远场区只剩下 Eθ 和 Hϕ 两个分量，这两个分量形成有效的能量流动，实现天线的能量辐射和传播。

下面研究一下能量传输，波印廷矢量

Wav=12Re[E→×H→∗]=12|a^ra^θa^ϕErEθEϕHr∗Hθ∗Hϕ∗|=12|a^ra^θa^ϕ0Eθ000Hϕ∗|=12EθHϕ∗a^r=12η(I04)2e−j2krr2(sinθ)2a^r

远场中电场和磁场的相位保持一致，而且只剩下可以传播的电磁能量分量。

需要说明的是，本文中基于无穷短偶极子获得的表达式直接带入半波长阵子进行计算并不是非常准确，但是可以给出一个直观的认识，让我们充分认识近远场不同场区的场分量变化，以及储能的能量流动的变化。

笔者水平有限，希望大家多多批评指正！