无人机测绘航线生成算法

1无人机测绘航线设计的基本概念

1.1像元

像元为相机感光元件的最小感光面，无人机航测遥感系统搭载的数码相机的像元大小为：

式中：L ——传感器长边（短边）大小（mm）；R ——长边（短边）像元个数（mm）。

1.2地面分辨率

照片单个像元所代表的地面尺寸。相同相机和镜头情况下，航高越大，地面分辨率越小；反之，航高越小，地面分辨率越大。

1.3航高

航高是指无人机相机镜头到地面的垂直距离，其大小直接影响无人机航测时实现的地面分辨率。无人机航测遥感系统中航高的确定跟成图比例尺、像元大小、地面分辨率有关，其相互关系为：

式中：摄影航高H，单位为米（m）； 镜头焦距f，单位为毫米（mm）；
             像元尺寸a，单位为毫米（mm）； 地面分辨率GSD，单位为米（m）。

一般来说，航测任务需要根据测区面积、特征、地形、精度等因素，来确定最佳的航高范围。航高设置合理，能够保证像片质量，提高地图准确度。

1.4航向重叠度和旁向重叠度

航向重叠度是指同一航线方向上的相邻照片所摄地面区域之间的重叠度，航向重叠度一般设置为60%-80%，最小不低于53%。

旁向重叠度则是相邻航线之间重叠地面区域的重叠度，旁向重叠度一般设置为15%-60%，最小不低于8%。

假设 qx、px 分别表示航向和旁向重叠部分的像片长度，L表示像幅长度，px、py 分别表示航向和旁向的重叠度，则：

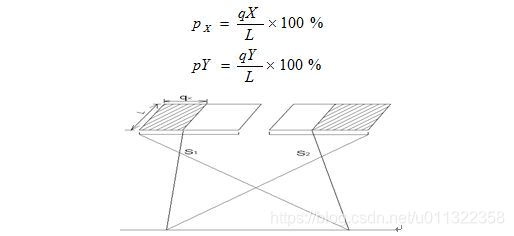
1.5基线长度

基线长度是同航线上连续两张曝光像片像主点之间的距离，其计算公式如下：

式中：基线长度B，单位为米（m）； 航向重叠率P； 纵向像幅地面尺寸，单位为米（m）。

1.6主航线方向

一般将测区第一条航测航线的飞行方向设为主航线方向。

无人机航测技术出现之前，面状区域型的航空摄影一般是以东西飞行为主，也可根据测区的范围特点采用南北飞行，例如测区的南北长度大于东西长度。对于道路、铁路、电力选线等工作时可以采用自由航线。现阶段，无人机航测的航线一般可根据当天天气风向、测区形状、无人机留空时间等等因素自由设计。

2代码实现

2.1基本类型定义

定义了基本的点、线、方向数据类型。

/DataDefinition//
//平面坐标点
function GPoint(x, y)
{
	return {
		x: x,
		y: y
	}
}
//经纬度点
function PointLatLng(Lng, Lat) {
	return {
		Lng: Lng,
		Lat: Lat
	}
}
//多边形方向枚举，顺时针、逆时针
const ClockDirection=
{
	Counterclockwise : 0,
	Clockwise : 1,
	None : 2
}
//线段定义（经纬度）
function LineSegement()
{
	this.number = 0;
	this.startPoint = new PointLatLng();
	this.endPoint = new PointLatLng();
}
//旋转点
class RotatePoint
{
	constructor()
	{
		this.number = 0;
		this.point = new PointLatLng();
		this.rotatepoint = new PointLatLng();
	}
}
//测区包围盒
class EnvelopeRect
{
	constructor()
	{
		this.LeftUpPoint = new PointLatLng();
		this.LeftDownPoint = new PointLatLng();
		this.RightUpPoint = new PointLatLng();
		this.RightDownPoint = new PointLatLng();

		this.LeftUpRotatePoint = new PointLatLng();
		this.LeftDownRotatePoint = new PointLatLng();
		this.RightUpRotatePoint = new PointLatLng();
		this.RightDownRotatePoint = new PointLatLng();
	}
}

2.2空间计算类

实现复杂坐标计算所必须的集中空间计算方法，包括：基本的角度转换、方位角计算、两点距离计算、时针方向计算、未知点位计算等等。

MapMethod/
class MapMethod
{
	static EARTH_RADIUS = 6378.137;//地球半径,km
	static EARTH_ARC = 111.199;//地球弧长,km
		
	static rad(d)
	{
		return d * Math.PI / 180.0;
	}

	static RadiansToDegrees(radians)
	{
		return radians * 180.0 / Math.PI;
	}

	static Azimuth(lat1, lng1, lat2, lng2)
	{
		let latitude1 = this.rad(lat1);
		let longitude1 = this.rad(lng1);
		let latitude2 = this.rad(lat2);
		let longitude2 = this.rad(lng2);
		let x = Math.cos(latitude1) * Math.sin(latitude2) - Math.sin(latitude1) * Math.cos(latitude2) * Math.cos(longitude2 - longitude1);
		return this.RadiansToDegrees(Math.atan2(Math.sin(longitude2 - longitude1) * Math.cos(latitude2), x) % (Math.PI * 2.0));
	}

	//已知一点经纬度A，和与另一点B的距离和方位角，求B的经纬度 
	//@param ptStart A的经纬度 
	//@param distance  AB距离（单位：千米） 
	//@param angel AB方位角 
	//@return B的经纬度 
	static ConvertDistanceToLatLng(ptStart, distance, angel)
	{
		let azimuth = this.rad(angel);
		// 将距离转换成经度的计算公式  
		let lng = ptStart.Lng + (distance * Math.sin(azimuth)) / (this.EARTH_ARC * Math.cos(this.rad(ptStart.Lat)));
		// 将距离转换成纬度的计算公式  
		let lat = ptStart.Lat + (distance * Math.cos(azimuth)) / this.EARTH_ARC;
		return new PointLatLng(lng, lat);
	}
	//计算多边形时钟方向（经纬度点集）
	static CalculateClockDirection(points, isYAxixToDown=false)
	{
		let i = 0, j = 0, k = 0;
		let count = 0;
		let z = 0.0;
		let  yTrans = isYAxixToDown ? (-1) : (1);

		if(points == null || points.length < 3)
		{
			return (ClockDirection.None);
		}

		let n = points.length;
		for(i = 0; i < n; i++)
		{
			j = (i + 1) % n;
			k = (i + 2) % n;
			z = (points[j].Lng - points[i].Lng) * (points[k].Lat * yTrans - points[j].Lat * yTrans);
			z -= (points[j].Lat * yTrans - points[i].Lat * yTrans) * (points[k].Lng - points[j].Lng);
			if (z < 0)
			{
				count--;
			}
			else if (z > 0)
			{
				count++;
			}
		}

		if (count > 0)
		{
			return (ClockDirection.Counterclockwise);
		}
		else if (count < 0)
		{
			return (ClockDirection.Clockwise);
		}
		else
		{
			return (ClockDirection.None);
		}
	}

	//计算两点距离（经纬度），米
	static GetDistance(startpoint,endpoint)
	{
		let latitude1 = this.rad(startpoint.Lat);
		let longitude1 = this.rad(startpoint.Lng);
		let latitude2 = this.rad(endpoint.Lat);
		let longitude2 = this.rad(endpoint.Lng);
		let num = Math.pow(Math.sin((latitude1 - latitude2) / 2.0), 2.0);
		let num2 = Math.pow(Math.sin((longitude1 - longitude2) / 2.0), 2.0);
		let d = Math.sqrt(num + Math.cos(latitude1) * Math.cos(latitude2) * num2);
		return