卷积神经网络CNN实战详解——图像分类中的CNN

卷积神经网络（CNN）是一种专门用于计算机视觉领域的深度学习架构。

它由多层组成，这些层能够自动从输入数据中学习层次化的特征，从简单的边缘模式开始，逐步深入到更复杂的结构，从而支持图像分类和物体检测等任务。

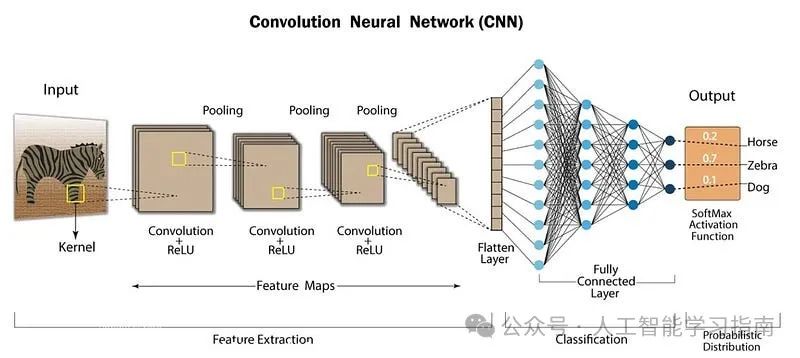
CNN架构

为什么我们需要CNN？

假设我们有一个6x6的矩阵，代表图像中的数字1。

import numpy as np

number_1_matrix = np.array([
    [0, 0, 1, 0, 0, 0],
    [0, 1, 1, 0, 0, 0],
    [1, 0, 1, 0, 0, 0],
    [0, 0, 1, 0, 0, 0],
    [0, 0, 1, 0, 0, 0],
    [0, 0, 1, 0, 0, 0]
])

import matplotlib.pyplot as plt

plt.imshow(number_1_matrix, cmap='gray', interpolation='nearest')
plt.title("Visualization of Number 1 Matrix")
plt.axis('off')
plt.show()

矩阵图

我们可以将这个矩阵转换为一列，作为常规神经网络的输入。

number_1_column = number_1_matrix.flatten().reshape(36, 1)

print(number_1_column)

"""
[[0]
 [0]
 [1]
 [0]
 [0]
 [0]
 [0]
 [1]
 [1]
 [0]
 [0]
 [0]
 [1]
 [0]
 [1]
 [0]
 [0]
 [0]
 [0]
 [0]
 [1]
 [0]
 [0]
 [0]
 [0]
 [0]
 [1]
 [0]
 [0]
 [0]
 [0]
 [0]
 [1]
 [0]
 [0]
 [0]]
"""

但对于6x6的图像，隐藏层的每个节点都需要进行36次权重计算。

然而，6x6的图像与现实场景相比非常小，想象一下，如果是一个1000x1000的图像，那么隐藏层的一个神经元就需要进行1,000,000次权重计算，这还只是单通道（如黑白图像）的情况。

对于彩色图像，每个神经元则需要3,000,000次计算，这在现实中是巨大且不切实际的。

此外，常规神经网络不一定能很好地处理如此大的输入。例如，如果图像仅移动一个像素，就无法保证在原始图像上训练的模型能在移动后的图像上表现良好。

# Shifting the number 1 to the right by one pixel
shifted_number_1_matrix = np.roll(number_1_matrix, shift=1, axis=1)

plt.imshow(shifted_number_1_matrix, cmap='gray', interpolation='nearest')
plt.title("Visualization of Shifted Number 1 Matrix")
plt.axis('off') 
plt.show()

偏移矩阵图

在图像中，相邻像素往往具有相似的颜色或模式，如蓝天中的多个蓝色像素相邻。

卷积神经网络（CNN）通过一次关注图像的小部分区域，利用这些局部模式进行设计。

这有助于网络学习重要的特征，如边缘或形状，这些特征是理解和分类整个图像的关键，使得CNN在图像识别任务中非常有效。

CNN如何实现图像分类的实用性？

• 减少输入节点数量：通过关注图像的小部分区域，使模型更高效。

• 处理图像小位移：即使物体稍有移动，模型仍能识别。

• 利用图像中的自然模式和相关性：如相似像素的聚集，以更好地理解和分类内容。

针对所有自学遇到困难的同学们，我帮大家系统梳理大模型学习脉络，将这份 LLM大模型资料 分享出来：包括LLM大模型书籍、640套大模型行业报告、LLM大模型学习视频、LLM大模型学习路线、开源大模型学习教程等, 😝有需要的小伙伴，可以 扫描下方二维码领取🆓↓↓↓

👉[CSDN大礼包🎁：全网最全《LLM大模型入门+进阶学习资源包》免费分享（安全链接，放心点击）]()👈

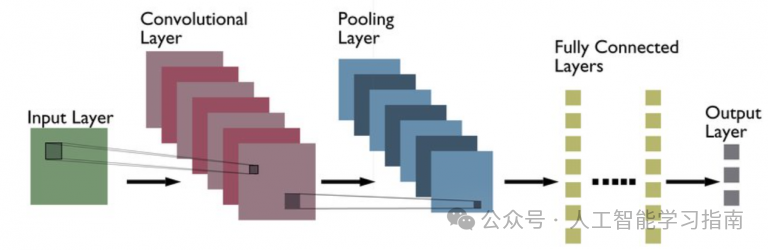
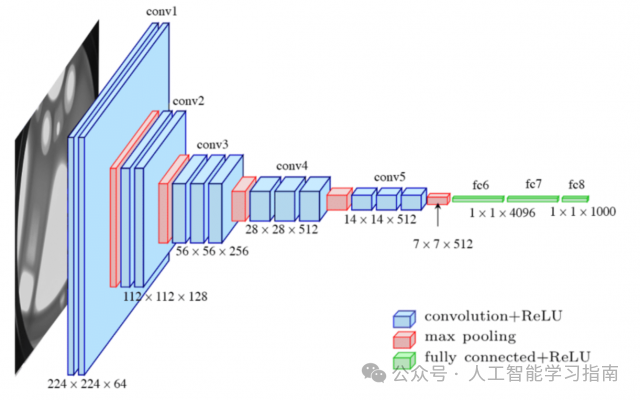
架构概览

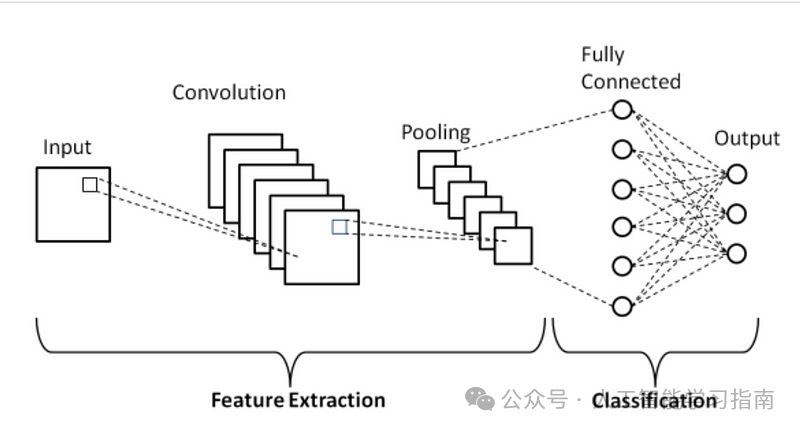
基础卷积神经网络（CNN）架构示意图

我们的输入层以数组的形式接收图像的像素作为输入。

卷积神经网络（CNN）首先执行的操作是滤波，这些滤波器作为滑动窗口在图像上移动，负责检测图像中的特征或模式。

边缘检测示例

检测到的这些特征会被传递到后续层，后续层可以进一步识别出标签。

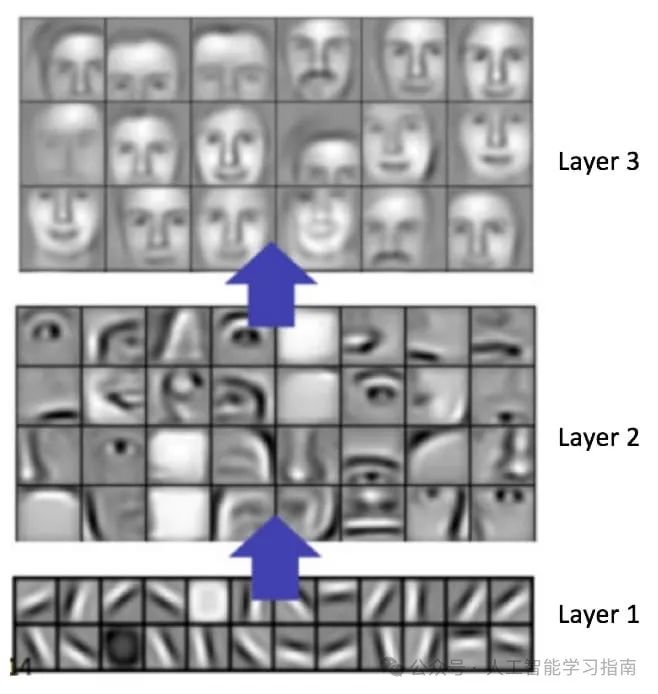
各层特征图

在卷积步骤中，滤波器被应用于输入图像，以创建特征图，这些特征图会突出显示重要的模式。

随后，ReLU（线性整流函数）通过将特征图中的负值替换为零来引入非线性。

池化操作则减少了特征图的空间大小，保留了最重要的信息，同时降低了计算复杂度。

展平操作将二维特征图转换为一维向量，以便为全连接层做准备。

全连接层将所有特征组合起来进行预测，该层中的每个神经元都与下一层中的每个神经元相连。

最后，输出层根据当前任务生成最终的分类或回归结果。

卷积操作

卷积步骤是CNN的核心，用于检测图像中的重要特征，如边缘。

在此步骤中，一个滤波器（通常为3x3像素的小矩阵）在图像上滑动以捕捉模式。

滤波器中的值在训练过程中通过反向传播进行调整，使网络能够学习识别不同物体所需的最重要模式。

现在，让我们对之前提到的6x6矩阵应用一个滤波器。

我们将使用经典的垂直边缘检测滤波器——Sobel滤波器。

# Define a classical vertical edge detection filter (Sobel filter)
vertical_edge_filter = np.array([
    [-1, 0, 1],
    [-2, 0, 2],
    [-1, 0, 1]
])

# Get the dimensions of the matrix and filter
matrix_height, matrix_width = number_1_matrix.shape
filter_height, filter_width = vertical_edge_filter.shape

# Calculate output dimensions
output_height = matrix_height - filter_height + 1
output_width = matrix_width - filter_width + 1

# Initialize the output matrix
convolution_output = np.zeros((output_height, output_width))

# Apply the convolution operation
for i in range(output_height):
    for j in range(output_width):
        region = number_1_matrix[i:i+filter_height, j:j+filter_width]
        convolution_output[i, j] = np.sum(region * vertical_edge_filter)

convolution_output

"""
array([[ 3., -2., -4.,  0.],
       [ 2., -1., -4.,  0.],
       [ 3.,  0., -4.,  0.],
       [ 4.,  0., -4.,  0.]])
"""

应用3x3滤波器后，结果是一个4x4的矩阵。

(n x n) * (f x f) = (n — f + 1) x (n — f + 1)

import matplotlib.pyplot as plt

# Display the original matrix
plt.subplot(1, 2, 1)
plt.imshow(number_1_matrix, cmap='gray', interpolation='nearest')
plt.title("Original Number 1 Matrix")
plt.axis('off')

# Display the convolution result
plt.subplot(1, 2, 2)
plt.imshow(convolution_output, cmap='gray', interpolation='nearest')
plt.title("Vertical Edge Detection")
plt.axis('off')

plt.show()

垂直边缘检测

在CNN的单层中，我们使用多个滤波器，每个滤波器检测图像的不同特征。

例如，一个滤波器可能检测水平边缘，另一个检测垂直边缘，还有一个可能检测圆形。

如果我们在一层中使用c个滤波器，那么对于灰度图像来说，其输出结果将是：

(n x n x 1) * (f x f x c) = (n — f + 1) x (n — f + 1) x c

对于彩色图像，我们有3个通道。对于单个滤波器而言：

(n x n x 1) * (f x f x 3) = (n — f + 1) x (n — f + 1) x 1

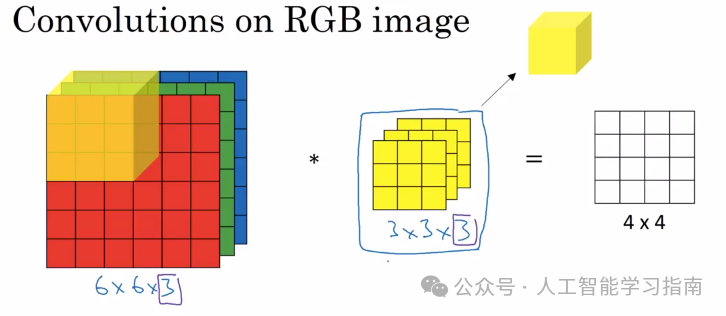
在卷积神经网络（CNN）中，当我们对图像应用滤波器时，实际上是在用一个小网格（即滤波器）扫描图像，以寻找特定的模式，如边缘或纹理。

每次滤波器在图像上移动到一个新位置时，它都会检查该部分图像与滤波器中的模式匹配程度如何。

这个过程会产生一个新的图像，称为特征图，它标出了原始图像中这些模式出现的位置。

特征图通过关注相互协作的邻近像素组，帮助网络理解和检测图像中的重要特征。

合并特征图的可视化

填充与步长

在卷积操作前，我们会在输入图像的边缘添加额外的像素，这一过程称为填充。

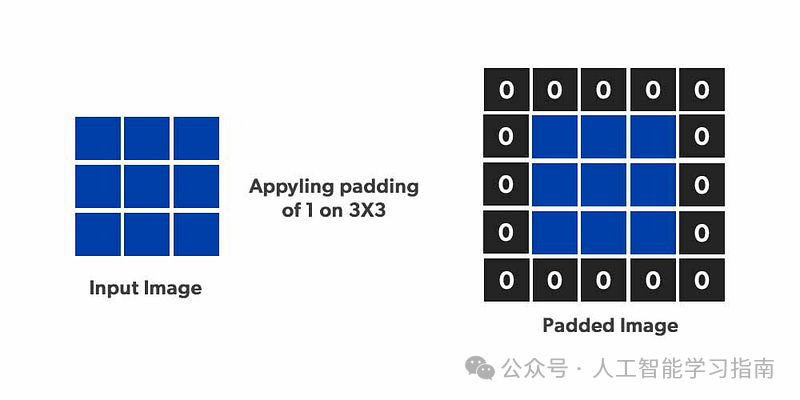
填充（Padding）示意图

进行填充主要有两大原因：

• 边缘应用：填充允许卷积核应用到图像的边缘。没有填充时，卷积核只能完全作用于图像的内部区域（对于角落仅一次，边缘则次数较少）。

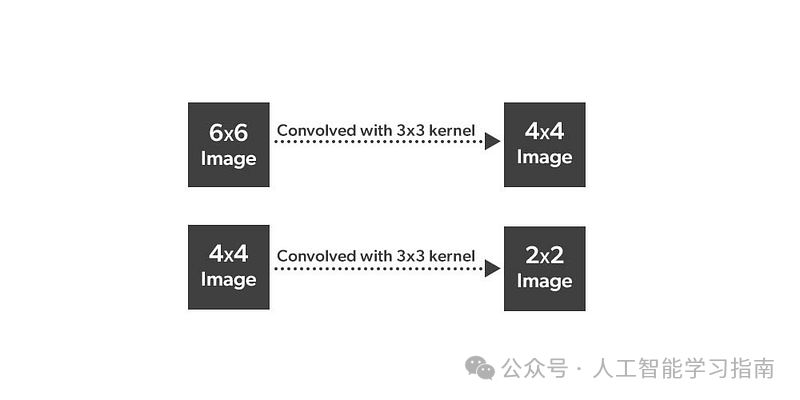
• 保持尺寸：每次卷积操作都会减小图像的大小。填充有助于保持输出特征图与输入图像尺寸相同。

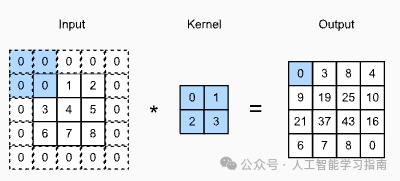
带填充的二维互相关运算

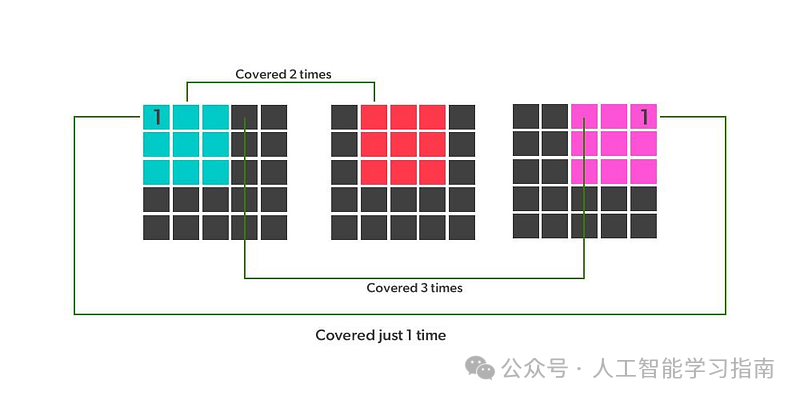
有效卷积：不添加填充，输出尺寸较小。

相同卷积：添加填充，输出尺寸与输入相同。其中，所需填充量p与卷积核大小f的关系为：

p = (f - 1) / 2。

步长：卷积过程中，卷积核在图像上每次移动的像素数。

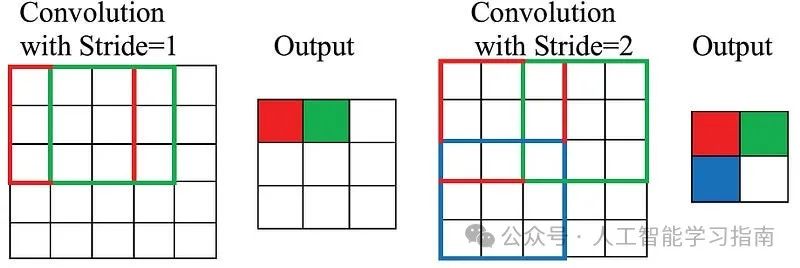
步长

若步长大于1，则卷积核会跳过一些像素，这样做既减小了输出特征图的尺寸，也使网络对图像中的微小偏移或细节不那么敏感。

• 填充帮助保持输出尺寸并捕获边缘信息。

• 步长控制卷积核在图像上的移动方式，影响特征图的尺寸和细节层次。

R eLU激活函数

卷积生成特征图后，通常会应用ReLU激活函数。ReLU即线性整流单元。

其操作简单：将特征图中的所有负值置为零，正值保持不变。这有助于网络仅关注重要特征（正值），并引入非线性，使模型能够学习更复杂的模式。

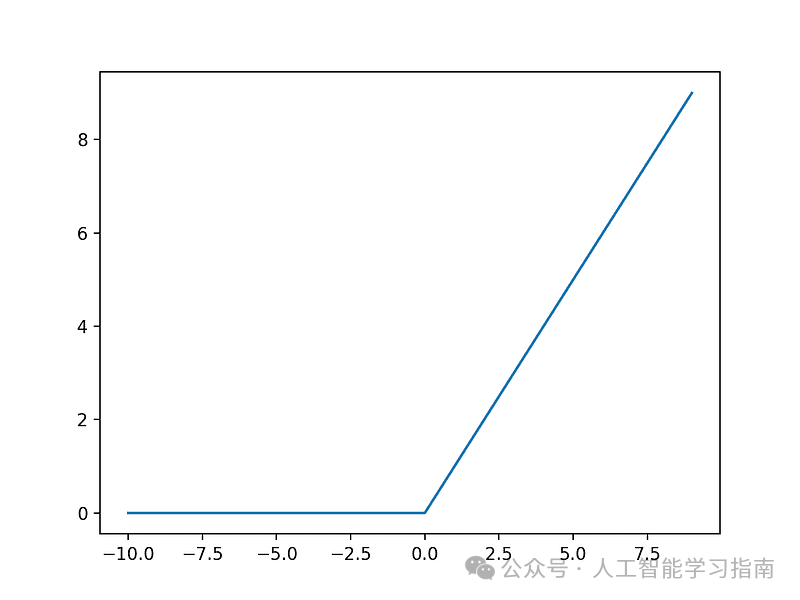
ReLU激活函数

import numpy as np
import matplotlib.pyplot as plt

number_1_matrix = np.array([
    [0, 0, 1, 0, 0, 0],
    [0, 1, 1, 0, 0, 0],
    [1, 0, 1, 0, 0, 0],
    [0, 0, 1, 0, 0, 0],
    [0, 0, 1, 0, 0, 0],
    [0, 0, 1, 0, 0, 0]
])

vertical_edge_filter = np.array([
    [-1, 0, 1],
    [-2, 0, 2],
    [-1, 0, 1]
])

# Get the dimensions of the matrix and filter
matrix_height, matrix_width = number_1_matrix.shape
filter_height, filter_width = vertical_edge_filter.shape

# Calculate output dimensions
output_height = matrix_height - filter_height + 1
output_width = matrix_width - filter_width + 1

# Initialize the output matrix
convolution_output = np.zeros((output_height, output_width))

# Apply the convolution operation
for i in range(output_height):
    for j in range(output_width):
        region = number_1_matrix[i:i+filter_height, j:j+filter_width]
        convolution_output[i, j] = np.sum(region * vertical_edge_filter)

# Apply ReLU activation function
relu_output = np.maximum(convolution_output, 0)

# Display the original matrix, convolution result, and ReLU result
plt.figure(figsize=(12, 4))

plt.subplot(1, 3, 1)
plt.imshow(number_1_matrix, cmap='gray', interpolation='nearest')
plt.title("Original Number 1 Matrix")
plt.axis('off')

plt.subplot(1, 3, 2)
plt.imshow(convolution_output, cmap='gray', interpolation='nearest')
plt.title("After Convolution")
plt.axis('off')

plt.subplot(1, 3, 3)
plt.imshow(relu_output, cmap='gray', interpolation='nearest')
plt.title("After ReLU Activation")
plt.axis('off')

plt.show()

最大池化

接下来，对卷积和ReLU步骤生成的特征图应用另一滤波器，该滤波器通常不重叠（步长大于1）地移动。

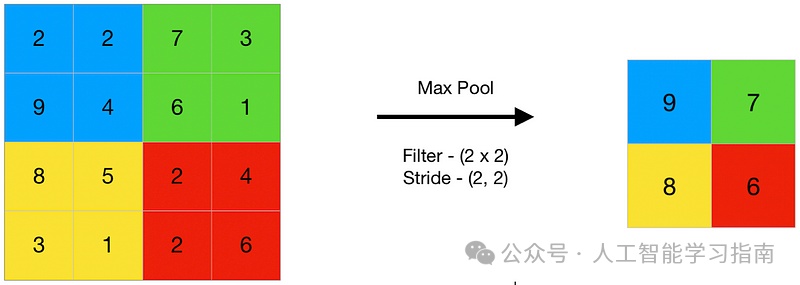
最大池化

这一过程称为池化，是一种下采样操作。

最大池化（Max Pooling）是在每个窗口位置选择该窗口内的最大值，并将其置于池化后的特征图中。

def max_pooling(feature_map, size=2, stride=2):
    # Get dimensions of the feature map
    h, w = feature_map.shape
    output_height = (h - size) // stride + 1
    output_width = (w - size) // stride + 1
    
    # Initialize the pooled output
    pooled_output = np.zeros((output_height, output_width))
    
    # Apply max pooling
    for i in range(0, h - size + 1, stride):
        for j in range(0, w - size + 1, stride):
            pooled_output[i//stride, j//stride] = np.max(feature_map[i:i+size, j:j+size])
    
    return pooled_output

max_pooled_output = max_pooling(relu_output)

plt.figure(figsize=(8, 4))

plt.subplot(1, 2, 1)
plt.imshow(relu_output, cmap='gray', interpolation='nearest')
plt.title("After ReLU Activation")
plt.axis('off')

plt.subplot(1, 2, 2)
plt.imshow(max_pooled_output, cmap='gray', interpolation='nearest')
plt.title("After Max Pooling")
plt.axis('off')

plt.show()

最大池化后

最大值代表滤波器在该区域检测到的最显著特征或“工作效果最佳”的位置。

最大池化保留了最强的激活，即滤波器检测到的最重要特征。

减少空间维度：降低特征图的高度和宽度，从而减少网络中的参数和计算量，有助于防止过拟合并加快处理速度。

展平

展平是将所有池化后的特征图（二维数组）转换为单个长的一维连续向量的过程。

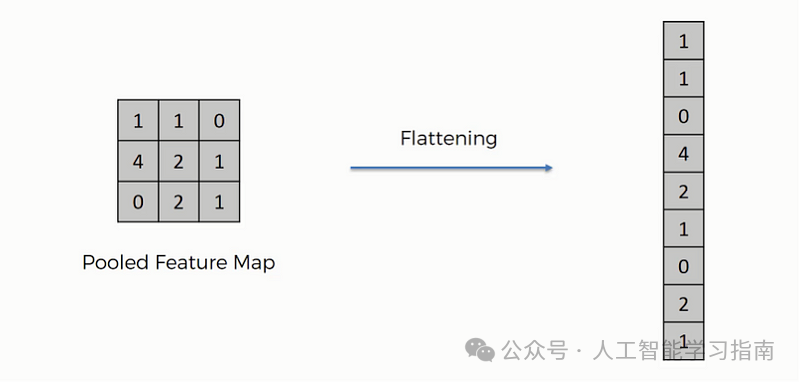
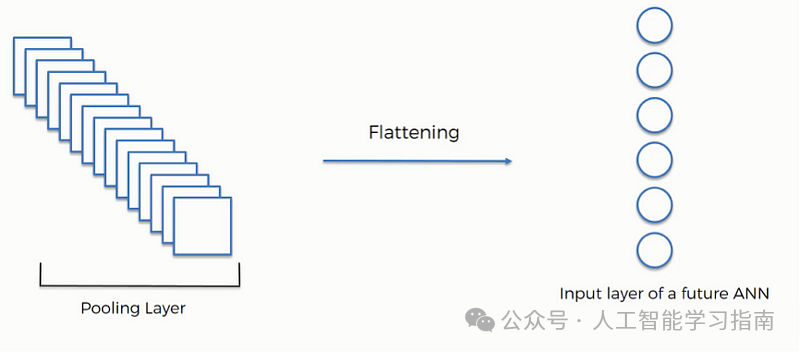
展平操作

这一转换是必要的，因为后续的全连接层（密集层）需要一维的输入形式。

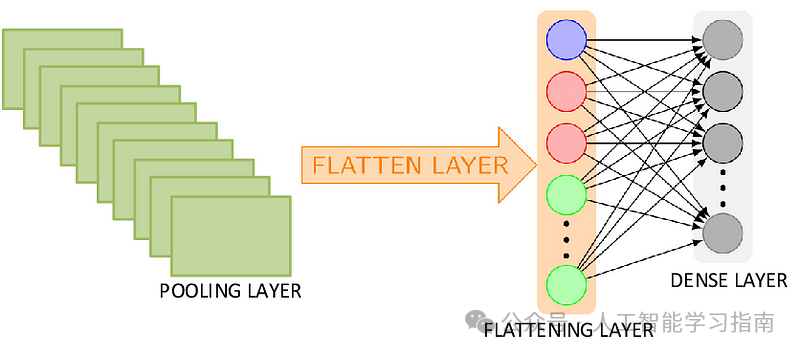
展平层

全连接层

全连接层结合卷积层和池化层学习到的特征来做出最终预测。在全连接层中，每个神经元都与前一层的每个神经元相连，这种密集连接允许该层考虑前一层特征的所有可能组合。

全连接层

输出层

输出层是网络的最后一层，提供预测或分类结果。

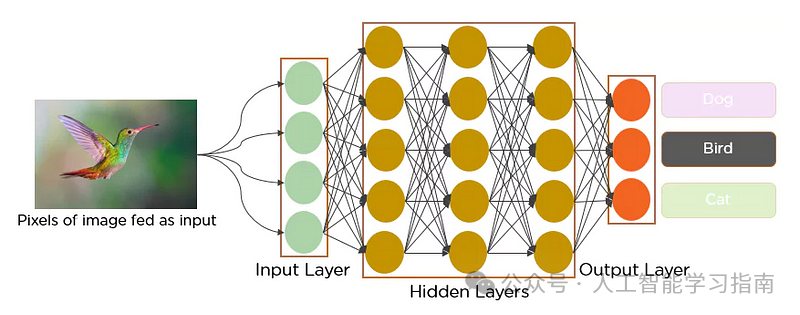
对于分类任务，神经元的数量等于可能的类别数。

输出层常使用softmax激活函数，将最后一个全连接层的原始输出值（称为logits）转换为概率分布。

反向传播

在前向传播中生成输出后，使用损失函数将输出与实际目标标签进行比较，生成一个表示网络预测总误差的标量值。

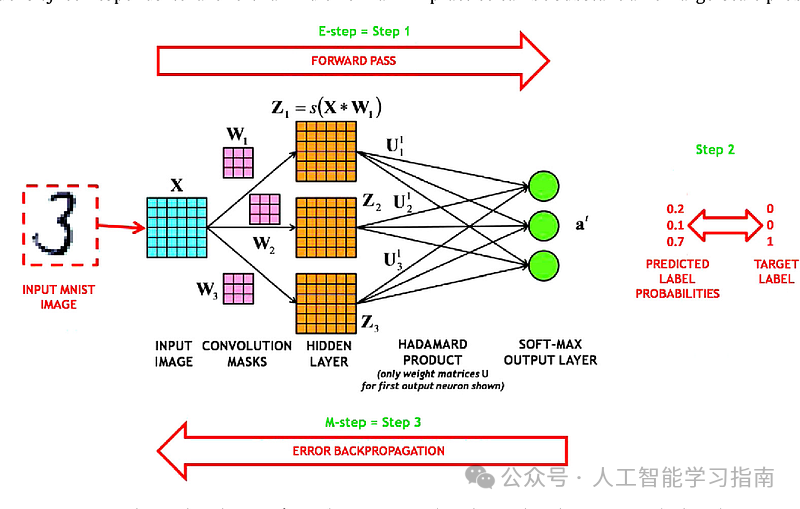
反向传播的目标是最小化这个损失，为此，网络计算损失函数关于网络中每个权重和偏置的梯度。

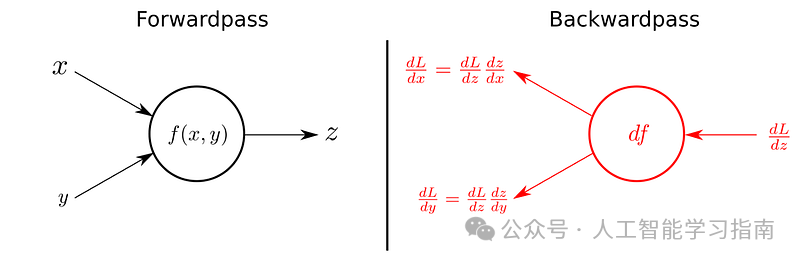
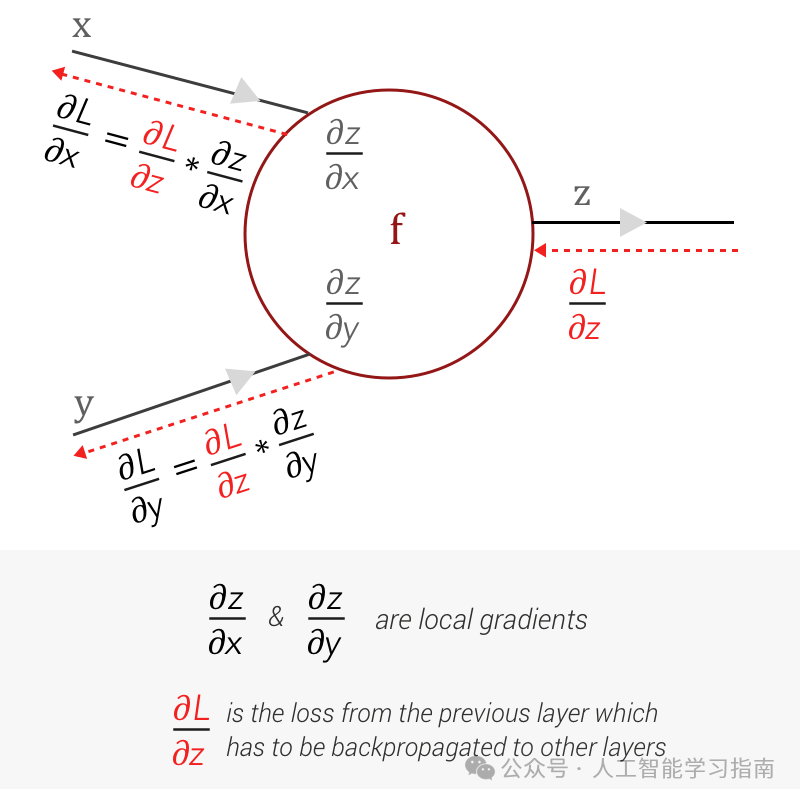
在卷积层中，梯度不仅针对卷积核的权重计算，还针对该层输入的像素计算。

池化层通常没有权重，因此梯度会直接通过，简单地回传到前向传播中它们来自的位置。

在全连接层中，梯度的计算与标准神经网络类似。

概述

• 卷积：检测特征。

• 填充与步长：控制尺寸和位置。

• ReLU：保留重要值。

• 最大池化：减小数据尺寸。

• 展平：将数据准备为一维形式。

• 全连接层：进行预测。

• 输出层：给出最终结果。

• 反向传播：通过减少误差来训练网络。

Python实现示例

您可以在这里下载数据集。

# Load data

X_train = np.loadtxt("Image Classification CNN Keras Dataset/input.csv", delimiter=",")
y_train = np.loadtxt("Image Classification CNN Keras Dataset/labels.csv", delimiter=",")

X_test = np.loadtxt("Image Classification CNN Keras Dataset/input_test.csv", delimiter=",")
y_test = np.loadtxt("Image Classification CNN Keras Dataset/labels_test.csv", delimiter=",")

print("X_train shape:", X_train.shape)
print("y_train shape:", y_train.shape)
print("X_test shape:", X_test.shape)
print("y_test shape:", y_test.shape)

"""
X_train shape: (2000, 30000)
y_train shape: (2000,)
X_test shape: (400, 30000)
y_test shape: (400,)
"""

# We need to process data.
X_train = X_train.reshape(len(X_train), 100, 100, 3)
X_test = X_test.reshape(len(X_test), 100, 100, 3)

y_train = y_train.reshape(len(y_train), 1)
y_test = y_test.reshape(len(y_test), 1)

print("X_train shape:", X_train.shape)
print("y_train shape:", y_train.shape)
print("X_test shape:", X_test.shape)
print("y_test shape:", y_test.shape)

"""
X_train shape: (2000, 100, 100, 3)
y_train shape: (2000, 1)
X_test shape: (400, 100, 100, 3)
y_test shape: (400, 1)
"""

X_train = X_train / 255.0
X_test = X_test / 255.0

数据集的形状为(2000, 30000)，这表示有2000个训练样本，每个样本由30,000个特征表示（这些特征对应于一个扁平化的图像）。

接下来，我们将这些图像数据重新塑形为4维数组，其中，100, 100, 3分别代表图像的高度、宽度和颜色通道数。

重塑后，X_train的形状变为(2000, 100, 100, 3)，意味着有2000张图像，每张图像的大小为100x100像素，且包含3个颜色通道。

然后，我们将图像的像素值除以255，以便将它们的值从0-255（图像数据的典型范围）缩放到0-1之间。

plt.imshow(X_train[0,:])
plt.show()

# the model architecture

model = Sequential()
model.add(Conv2D(32, (3, 3), activation='relu', input_shape=(100, 100, 3)))
model.add(MaxPooling2D((2, 2)))

model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D((2, 2)))

model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1, activation='sigmoid'))

接下来，我们开始训练模型。

model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

history = model.fit(X_train, y_train, epochs=15, batch_size=32)

"""
Epoch 1/15
63/63 [==============================] - 3s 34ms/step - loss: 1.0101 - accuracy: 0.5140
Epoch 2/15
63/63 [==============================] - 2s 36ms/step - loss: 0.7403 - accuracy: 0.5360
Epoch 3/15
63/63 [==============================] - 2s 34ms/step - loss: 0.6731 - accuracy: 0.5875
Epoch 4/15
63/63 [==============================] - 2s 31ms/step - loss: 0.6214 - accuracy: 0.6725
Epoch 5/15
63/63 [==============================] - 2s 31ms/step - loss: 0.5658 - accuracy: 0.7055
Epoch 6/15
63/63 [==============================] - 2s 32ms/step - loss: 0.5183 - accuracy: 0.7555
Epoch 7/15
63/63 [==============================] - 2s 32ms/step - loss: 0.4621 - accuracy: 0.7855
Epoch 8/15
63/63 [==============================] - 2s 33ms/step - loss: 0.4077 - accuracy: 0.8125
Epoch 9/15
63/63 [==============================] - 2s 32ms/step - loss: 0.3721 - accuracy: 0.8405
Epoch 10/15
63/63 [==============================] - 2s 33ms/step - loss: 0.3268 - accuracy: 0.8530
Epoch 11/15
63/63 [==============================] - 2s 34ms/step - loss: 0.3094 - accuracy: 0.8745
Epoch 12/15
63/63 [==============================] - 2s 32ms/step - loss: 0.2918 - accuracy: 0.8900
Epoch 13/15
63/63 [==============================] - 2s 32ms/step - loss: 0.2383 - accuracy: 0.9060
Epoch 14/15
63/63 [==============================] - 2s 33ms/step - loss: 0.2307 - accuracy: 0.9220
Epoch 15/15
63/63 [==============================] - 2s 32ms/step - loss: 0.2440 - accuracy: 0.9250

在最后一个训练周期中，我们达到了0.9250的准确率。现在，让我们来评估测试数据的表现。

model.evaluate(X_test, y_test)

"""
[1.631995439529419, 0.6424999833106995]
"""
# [loss, accuracy]

测试数据上的准确率为0.64。这显然是一个过拟合的情况:)

最后，让我们进行预测。

plt.imshow(X_test[3, :])
plt.show()

y_pred = model.predict(X_test[3, :].reshape(1, 100, 100, 3))
if y_pred[0][0] > 0.5:
    pred = "Cat"
else:
    pred = "Dog"
print(y_pred)
print(pred)

"""
1/1 [==============================] - 0s 15ms/step
[[0.00018852]]
Dog
"""

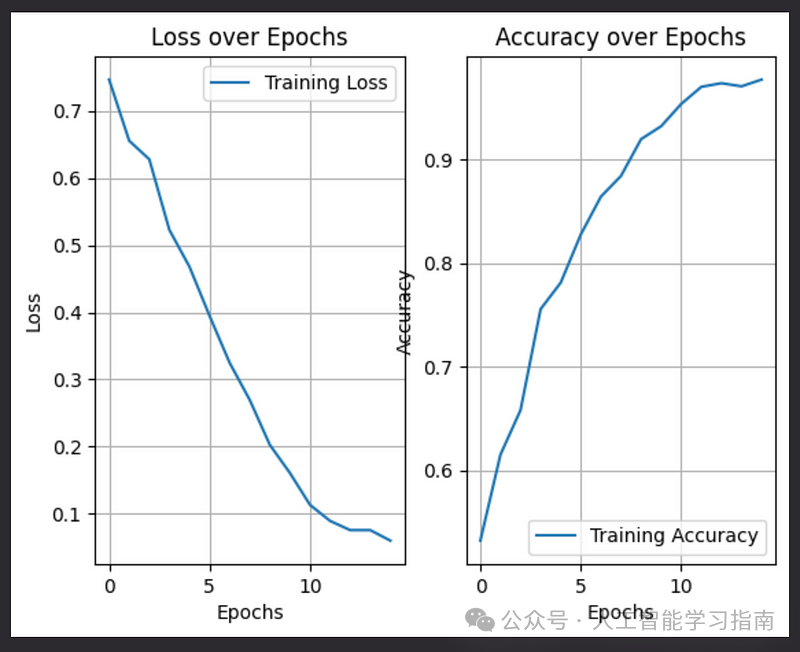
# Plot the loss
plt.subplot(1, 2, 1)
plt.plot(history.history['loss'], label='Training Loss')
plt.title('Loss over Epochs')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)

# Plot the accuracy
plt.subplot(1, 2, 2)
plt.plot(history.history['accuracy'], label='Training Accuracy')
plt.title('Accuracy over Epochs')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.grid(True)

plt.show()

读者福利：如果大家对大模型感兴趣，这套大模型学习资料一定对你有用

对于0基础小白入门：

如果你是零基础小白，想快速入门大模型是可以考虑的。

一方面是学习时间相对较短，学习内容更全面更集中。
二方面是可以根据这些资料规划好学习计划和方向。

包括：大模型学习线路汇总、学习阶段，大模型实战案例，大模型学习视频，人工智能、机器学习、大模型书籍PDF。带你从零基础系统性的学好大模型！

😝有需要的小伙伴，可以保存图片到wx扫描二v码免费领取【保证100%免费】🆓

👉AI大模型学习路线汇总👈

大模型学习路线图，整体分为7个大的阶段：（全套教程文末领取哈）

第一阶段： 从大模型系统设计入手，讲解大模型的主要方法；

第二阶段： 在通过大模型提示词工程从Prompts角度入手更好发挥模型的作用；

第三阶段： 大模型平台应用开发借助阿里云PAI平台构建电商领域虚拟试衣系统；

第四阶段： 大模型知识库应用开发以LangChain框架为例，构建物流行业咨询智能问答系统；

第五阶段： 大模型微调开发借助以大健康、新零售、新媒体领域构建适合当前领域大模型；

第六阶段： 以SD多模态大模型为主，搭建了文生图小程序案例；

第七阶段： 以大模型平台应用与开发为主，通过星火大模型，文心大模型等成熟大模型构建大模型行业应用。

👉大模型实战案例👈

光学理论是没用的，要学会跟着一起做，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。

👉大模型视频和PDF合集👈

观看零基础学习书籍和视频，看书籍和视频学习是最快捷也是最有效果的方式，跟着视频中老师的思路，从基础到深入，还是很容易入门的。

👉学会后的收获：👈

• 基于大模型全栈工程实现（前端、后端、产品经理、设计、数据分析等），通过这门课可获得不同能力；

• 能够利用大模型解决相关实际项目需求： 大数据时代，越来越多的企业和机构需要处理海量数据，利用大模型技术可以更好地处理这些数据，提高数据分析和决策的准确性。因此，掌握大模型应用开发技能，可以让程序员更好地应对实际项目需求；

• 基于大模型和企业数据AI应用开发，实现大模型理论、掌握GPU算力、硬件、LangChain开发框架和项目实战技能， 学会Fine-tuning垂直训练大模型（数据准备、数据蒸馏、大模型部署）一站式掌握；

• 能够完成时下热门大模型垂直领域模型训练能力，提高程序员的编码能力： 大模型应用开发需要掌握机器学习算法、深度学习框架等技术，这些技术的掌握可以提高程序员的编码能力和分析能力，让程序员更加熟练地编写高质量的代码。

👉获取方式：

😝有需要的小伙伴，可以保存图片到wx扫描二v码免费领取【保证100%免费】🆓