Huffman树

        Huffman Tree，中文名是哈夫曼树或霍夫曼树，它是最优二叉树。哈夫曼树的应用很广，在不同的应用中叶子结点的值可以有不同的解释。当哈夫曼树应用到信息编码中，权值可看成是某个符号出现的频率：当应用到判定过程中，可看成是某类数据出现的频率；当应用到排序问题中，可看成是已排好次序而待合并的序列的长度等等。

一、Huffman树基本概念

        给定n个权值作为n个叶子结点，构造一棵二叉树，若树的带权路径长度达到最小，则这棵树被称为哈夫曼树（Huffman Tree）。

这里有几个要先了解的概念：
（1）什么是路径

（2）什么是路径长度
（3）什么是结点的权

（4）什么是带权路径长度

（5）什么是结点的带权路径长度

（6）什么是树的带权路径长度

（7）如何构造具有最短带权路径长度的树

接下来我们逐一讲解。

1.路径和路径长度

        在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。

        通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

        如上图中，从根结点100出发 ，到达结点100和80的路径长度是1，到达结点50和30的路径长度是2，到达结点20和10的路径长度是3。

2.结点的权及带权路径长度

        若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。

        结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。

        同样在上图中，结点20的路径长度是3，它的带权路径长度=路径长度 * 权 = 3 * 20 = 60。

3.树的带权路径长度

        树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。

        同样在上图中，树的WPL= 1*100 +2*50+ 3*20 + 3*10 = 100 + 100 + 60 + 30 = 290

4.比较两棵二叉树WPL

        以下两棵树，具有相同的叶子结点，但是它们的构造不一样，则它们的WPL也可能不同。

        树的WPL=2*10 + 2*20 + 2*50 + 2*100 = 360

        树的WPL=1*100 +2*50+ 3*20 + 3*10=290

        显然，由于排列的不同，使得树的带权路径长度也出现了不同。所以如何构造出来的二叉树是一颗最优的二叉树，是一个需要思考的问题。

二、哈夫曼树的构造

1.哈夫曼树的构造规则

        假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，哈夫曼树的构造规则为：

（1）将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

（2）在森林中选出根结点权值最小的两棵树进行合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

（3）从森林中删除选取的两棵树，并将新树加入森林；

（4）重复（2）、（3）步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

2.哈夫曼树的构造

        以{5,6,7,8,15}为例，来构造一棵哈夫曼树。

（1）哈夫曼树构造实例步骤一

        这里有5棵树构造的森林

（2）哈夫曼树构造实例步骤二

        选择森林中的权值最小的两棵树，以它们为叶子，构建一个新树，树的根的权值为两棵树的权值只和。此时，森林中就剩下了4棵树。

（3）哈夫曼树构造实例步骤三

        接下来在从选择森林中继续选择两颗权值最小的树，以它们为叶子，构建一个新树，树的根的权值为两棵树的权值只和。构造完成之后森林中就剩下了3棵树。

        当然这里的方法不唯一，可以是先选一颗最小权值的树跟已经构造的树继续合成，也可以像现在这样，构造新树。

（4）哈夫曼树构造实例步骤四

        同样的方式，继续构造。

（5）哈夫曼树构造实例步骤五

        最后构造成一棵树，此时的树就是一颗具有最小带权路径长度的二叉树，即哈夫曼树。

3.哈夫曼树的构造算法实现

        创建哈夫曼树的算法实现，在构造哈夫曼树的过程中，我们是每次都是取森林中的具有最小权值的结点，为了更好的实现，所以第一步，我们应该先将所有结点的权值进行从小到大的排序，将排序好的所有结点都放在一个队列中，让后按先进先出的顺序逐一从队列中取出剩余结点中具有最小权值的结点。

//创建哈夫曼树

public void createTree() {

          //创建优先队列

         Queue<Node>q1=new PriorityQueue<Node>(

                    new Comparator<Node>() {

        public int compare(Node o1, Node o2) {

return o1.count-o2.count;

}});

         //将结点列表加入到队列中

         q1.addAll(nodes);

         

         //如果队列不为空

         while(!q1.isEmpty()){

//出队一个结点

Node n1=q1.poll();

//出队一个结点

Node n2=q1.poll();



             //通过两个结点创建父结点

             Node parent=new Node(n1,n2,n1.count+n2.count);



             //如果队列为空

             if(q1.isEmpty()){

            root=parent;

                 return;

             }

        //将父结点加入到队列中

             q1.add(parent);

         }

     }

代码说明：
（1）先将所有数字进行从小到大排序，并存放在队列中；

（2）从队列中逐一出队最小的元素，构造新的树；

（3）新树的父结点为两个子结点的权值之和；

（4）重复构建，直到队列为空。

三、Huffman树的应用

1.优化判断过程

        将百分制转换成五级制的算法。显然，此算法很简单，只需利用if语句描述即可。

        如果学生规模很大，该算法需反复多次执行，就应该考虑算法执行的时间问题。在实际应用中，学生的成绩呈正态分布，大部分在70~89分之间，优秀和不及格的概率较小。假设不及格、及格、中、良、优的百分比为5％、12%、40%、35%、8%，则上述算法80%以上的成绩需要进行三次或三次以上的比较才能得到结果。

        若以这些百分比值5,12,40,35,8为权值，使用哈夫曼算法来构造一棵判定树，则得到的判定过程，可使多数成绩经过较少的比较即可得到结果。

   未使用哈夫曼树判定

使用哈夫曼树判定

        使得具有最大占比的成绩的比较次数最少，第二多认识的成绩，比较的次数第二少，一次类推。就可以最大限度的减少了成绩在实现分级时最少的比较次数，从而达到了优化程序的目的。

2.哈夫曼编码

（1）算法分析

        在数据通信中，需要将传送的文字转换成二进制的字符串，用0，1码的不同排列来表示字符。假如，需传送的报文为“AFTER DATA EAR ARE ART AREA”，这里用到的字符集为“A，E，R，T，F，D”，各字母出现的次数为{8，4，5，3，1，1}，现要求为这些字母设计编码。

        要区别6个字母，最简单的二进制编码方式是等长编码，固定采用3位二进制，可分别用000、001、010、011、100、101对“A，E，R，T，F，D”进行编码发送。

        在实际应用中，各个字符的出现频度或使用次数是不相同的，让使用频率高的用短码，使用频率低的用长码，以优化整个报文编码。这种就是非等长编码。设计时能够保证任何一个字符的编码都不是同一字符集中另一个字符的编码的前缀，符合此要求的编码称为前缀编码。

（2）哈夫曼编码

        即根据字符的不同频率来设计一种非等长的编码，使得在表达相同意思的报文时使用更短的字符。以下分别是：结点数据结构class TreeNode 和有参数构造方法。

public class TreeNode {

Character ch;   //ch存储当前结点字符

int val; //若在构建二叉树的过程中该结点为左结点，则val=0,反之，val=1

int freq;       // 存储字符出现的频次

TreeNode left;  // 左结点

TreeNode right; // 右结点

public TreeNode() {

 }



//有参数构造方法

public TreeNode(Character ch, int val, int freq, TreeNode left, TreeNode right) {

this.ch = ch;

this.val = val;

this.freq = freq;

this.left = left;

this.right = right;



  }

}

3.哈夫曼编码的实现过程

        以下是字符级每个字符的结点结构：

        Val：用于标识构建二叉树的过程中该结点为左结点val=0，还是右结点val=1；

        Freq：字符对应的出现的次数。

（1）初始化二叉树结点

（2）选择最小频率的两个结点组成一颗二叉树

（3）继续选择最小频率的两个结点组成一颗二叉树

（4）哈夫曼编码最终二叉树

4.哈夫曼编码表和传送长度

符哈夫曼编码表

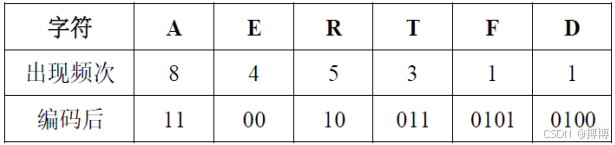
使用哈夫曼编码的报文的最短传送长度为：  

           6

     L=WPL=(wklk)=4×2+5×2+8×2+3×3+1×4+1×4=51

        k=1

若采用等长编码，报文的传送长度为：L=8×3+4×3+5×3+3×3+1×3+1×3=66

5.java代码实现

哈夫曼编码生成树代码。

// 遍历dataMap,初始化二叉树结点，并将所有初始化后的结点放到nodeList中，并进行排序

LinkedList<TreeNode> nodeList = new LinkedList<TreeNode>();

for (Map.Entry<Character, Integer> entry : dataMap.entrySet()) {

Character ch = entry.getKey();

int freq = entry.getValue();

int val = 0;

TreeNode tmp = new TreeNode(ch, val, freq, null, null);

odeList.add(tmp);

}

// 对存放结点的链表进行排序，方便后续进行组合

Collections.sort(nodeList, new Comparator<TreeNode>() {

             public int compare(TreeNode t1, TreeNode t2) {

return t1.freq - t2.freq;

}

});

while (nodeList.size() > 0) {

       TreeNode t1 = nodeList.removeFirst();

       TreeNode t2 = nodeList.removeFirst();

       // 左子树的val赋值为0，右子树的val赋值为1

        t1.val = 0;    t2.val = 1;

       // 将取出的两个结点进行合并

       if (nodeList.size() == 0) {

// 此时代表所有结点合并完毕，返回结果

           root = new TreeNode(null, 0, t1.freq + t2.freq, t1, t2);

       } else {

// 此时代表还有可以合并的结点

       TreeNode tmp = new TreeNode(null, 0, t1.freq + t2.freq, t1, t2);

  if (tmp.freq > nodeList.getLast().freq) {            nodeList.addLast(tmp);

} else {            

for (int i = 0; i < nodeList.size(); i++) {

      int tmpFreq = tmp.freq;

          if (tmpFreq <= nodeList.get(i).freq) {

nodeList.add(i, tmp);

        break;

      }

       }

    }

  }

 }

 // 返回建立好的二叉树根结点

 return root;

}

继续实践？

        假设用于通讯电文仅有8个字母A、B、C、D、E、F、G组成，字母在电文出现的频率分别为：0.07，0.19，0.02，0.06，0.32，0.03，0.21，0.10。请为这8个字母设计哈夫曼编码。