matplotlib.pyplot包中包含了简单绘图功能。调用的函数都会改变当前的绘图。将绘图存入文件或使用show函数显示出来。
1、绘制多项式函数
多项式函数是变量的整数次冥与系数的乘积之和,可以用下面的公式表示:
由于多项式函数只包含加法和乘法运算,因此计算容易,并且可以用于计算其他数学函数的近似值。在Numpy中,多项式函数的系数可以用一维数组表示,如f(x) =x^3-2x+1,则可以表示为数组:
其中a[0]是最高次项,a[-1]是常数项。
系数可以通过poly1d( )函数转换为多项式对象,此对象可以像函数一样调用,它返回多项式函数的值。
对 poly1d( )对象进行加减乘除运算 ,相当于对应多项式函数进行计算,如:
上面的商式为:x^2-x-1,余式为2。
多项式对象的deriv( )和integ( )方法分别用于计算多项式函数的微分和积分 ,如:
多项式函数的根可以用roots( )计算 :
而 poly()函数可以将根转换为多项式的系数 ,如:
参考:http://blog.csdn.net/kezunhai/article/details/46271165
import numpy as np
import matplotlib.pyplot as plt
# (1) 以自然数序列作为多项式的系数,使用poly1d函数创建多项式。
func = np.poly1d(np.array([1, 2, 3, 4]).astype(float))
# (2) 使用NumPy的linspace函数创建x轴的数值,在-10和10之间产生30个均匀分布的值。
x = np.linspace(-10, 10, 30)
# (3) 计算我们在第一步中创建的多项式的值。
y = func(x)
# (4) 调用plot函数,这并不会立刻显示函数图像。
plt.plot(x, y)
# (5) 使用xlabel函数添加x轴标签。
plt.xlabel('x')
# (6) 使用ylabel函数添加y轴标签。
plt.ylabel('y(x)')
# (7) 调用show函数显示函数图像。
plt.show()2、绘制多项式函数及其导函数
import numpy as np
import matplotlib.pyplot as plt
# (1) 创建多项式函数及其导函数。
func = np.poly1d(np.array([1, 2, 3, 4]).astype(float))
func1 = func.deriv(m=1)
x = np.linspace(-10, 10, 30)
y = func(x)
y1 = func1(x)
# (2)以两种不同风格绘制多项式函数及其导函数:红色圆形和绿色虚线。你可能无法在本书的印刷版中看到彩色图像,因此只能自行尝试绘制图像。
plt.plot(x, y, 'ro', x, y1, 'g--')
plt.xlabel('x')
plt.ylabel('y')
plt.show()3、绘制多项式函数及其导函数
subplot函数创建第一个子图。该函数的第一个参数是子图的行数,第二个参数是子图的列数,第三个参数是一个从1开始的序号。另一种方式是将这3个参数结合成一个数字,如311。
import numpy as np
import matplotlib.pyplot as plt
# (1) 创建多项式函数及其导函数。
func = np.poly1d(np.array([1, 2, 3, 4]).astype(float))
x = np.linspace(-10, 10, 30)
y = func(x)
func1 = func.deriv(m=1)
y1 = func1(x)
func2 = func.deriv(m=2)
y2 = func2(x)
# (2) 使用subplot函数创建第一个子图。该函数的第一个参数是子图的行数,第二个参数是子图的列数,第三个参数是一个从1开始的序号。另一种方式是将这3个参数结合成一个数
# 字,如311。这样,子图将被组织成3行1列。设置子图的标题为Polynomial,使用红色实线绘制。
plt.subplot(311)
plt.plot(x, y, 'r-')
plt.title("Polynomial")
# (3) 使用subplot函数创建第二个子图。设置子图的标题为First Derivative,使用蓝色三角形绘制。
plt.subplot(312)
plt.plot(x, y1, 'b^')
plt.title("First Derivative")
# (4) 使用subplot函数创建第三个子图。设置子图的标题为Second Derivative,使用绿色圆形绘制。
plt.subplot(313)
plt.plot(x, y2, 'go')
plt.title("Second Derivative")
plt.xlabel('x')
plt.ylabel('y')
plt.show()
4、三维空间中绘图
我们将在三维空间中绘制一个简单的三维函数。
z = x2 =y2
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
fig = plt.figure()
# (1) 我们需要使用3d关键字来指定图像的三维投影。
ax = fig.add_subplot(111, projection='3d')
# (2) 我们将使用meshgrid函数创建一个二维的坐标网格。这将用于变量x和y的赋值。
u = np.linspace(-1, 1, 100)
x, y = np.meshgrid(u, u)
z = x ** 2 + y ** 2
# (3) 我们将指定行和列的步幅,以及绘制曲面所用的色彩表(color map)。步幅决定曲面上“瓦片”的大小,而色彩表的选择取决于个人喜好。
ax.plot_surface(x, y, z, rstride=4, cstride=4, cmap=cm.YlGnBu_r)
plt.show()
使用contour函数创建一般的等高线图。对于色彩填充的等高线图,可以使用contourf绘制。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
fig = plt.figure()
ax = fig.add_subplot(111)
u = np.linspace(-1, 1, 100)
x, y = np.meshgrid(u, u)
z = x ** 2 + y ** 2
ax.contourf(x, y, z)
plt.show()6、制作动画
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
fig = plt.figure()
ax = fig.add_subplot(111)
N = 10
x = np.random.rand(N)
y = np.random.rand(N)
z = np.random.rand(N)
# (1) 我们将用不同颜色的圆形、小圆点和三角形来绘制三个数据集中的数据点。
circles, triangles, dots = ax.plot(x, 'ro', y, 'g^', z, 'b.')
ax.set_ylim(0, 1)
plt.axis('off')
# (2) 下面的函数将被定期调用以更新屏幕上的内容。我们将随机更新两个数据集中的y坐标值。
def update(data):
circles.set_ydata(data[0])
triangles.set_ydata(data[1])
return circles, triangles
# (3) 使用NumPy生成随机数。
def generated():
while True: yield np.random.rand(2, N)
anim = animation.FuncAnimation(fig, update, generated(), interval=150)
plt.show()待续!








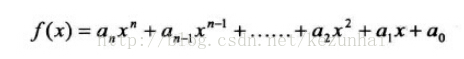















 777
777

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










