decision tree的结点纯度计算方法

最新推荐文章于 2024-04-15 21:07:05 发布

原创最新推荐文章于 2024-04-15 21:07:05 发布 · 2.6k 阅读

4 ·

CC 4.0 BY-SA版权

决策树同时被 2 个专栏收录

1 篇文章

订阅专栏

机器学习

0 篇文章

订阅专栏

本文探讨了决策树中用于衡量结点纯度的两种方法——Gini指数和熵。通过计算公式，解释了如何确定根结点以及如何评估属性的纯度。纯度越高，表示结点分类的确定性越强，适合作为划分依据。当概率相等时，纯度最低，而概率趋向0或1时，纯度最高。

决策树是一种机器学习领域的分类方法，首先通过训练集来构建决策树，并在测试集上使用决策树对测试数据进行分类。本文主要讲解对各结点的纯度计算方法。

要确定决策树的根结点，要对不同属性进行纯度计算。主要有两种计算方法。

1. Gini

公式： $\mathit{GINI(t)} = 1-\sum[\mathit{p}(j|t)]^{2}$

$\mathit{p}(j|t)$ 是指在结点t的相对频率。

例如，某一属性按照C1，C2两类的分类情况如下：

C1	0
C2	6

对于这种情况，使用上述公式可得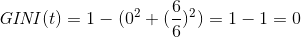： $\mathit{GINI}(t) = 1-(0^{2}+(\frac{6}{6})^{2}) = 1-1 = 0$ 。对于这种情况，GINI值取到最小值，说明这种情况不确定性最低，纯度最高。

又或者是另一种情况：

C1	3
C2	3

对于这种情况，可得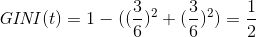： $\mathit{GINI}(t) = 1-((\frac{3}{6})^{2}+(\frac{3}{6})^{2}) = \frac{1}{2}$ 。结点分到每一类的可能性相同，不确定最高，纯度最低。这种属性显然不适合作为决策树的分类结点。

我们选择纯度最高的属性作为根结点。

每种属性继续分为若干个儿子，如何计算这种属性的GINI值呢？

公式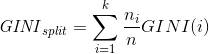： $\mathit{GINI}_{split} = \sum_{i=1}^{k}\frac{n_{i}}{n}GINI(i)$

假设某种属性B又可分为N1，N2两个结点。

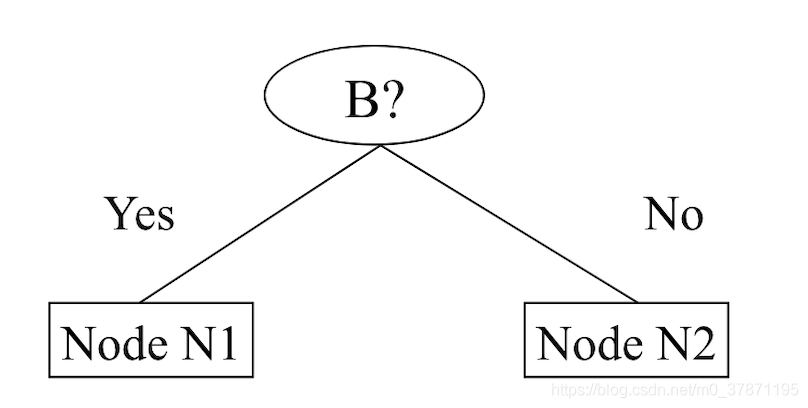
每个结点继续按照C1，C2分类

	N1	N2
C1	5	1
C2	2	4

计算N1，N2GINI值

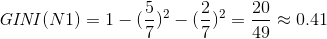
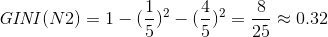
$\mathit{GINI}(N1) = 1-(\frac{5}{7})^{2}-(\frac{2}{7})^{2} = \frac{20}{49} \approx 0.41$ $\mathit{GINI}(N2) = 1-(\frac{1}{5})^{2}-(\frac{4}{5})^{2} = \frac{8}{25} \approx 0.32$

因此，

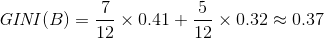
$\mathit{GINI}(B) = \frac{7}{12}\times 0.41 + \frac{5}{12} \times 0.32 \approx 0.37$

这样我们获得了B属性的纯度值，可能别的属性会不止分成两个结点，但计算方法是一样的。

2. Entropy

公式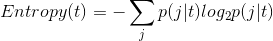： $Entropy(t) = -\sum_{j}^{ }p(j|t)log_{2} p(j|t)$

计算方法和GINI类似：

某一属性分为若干自结点，他的entropy计算方法也和GINI相同，都是按照各个结点所占权重进行计算。

3. 总结

两种对于纯度计算的方法都是对于结点分类纯度的体现。对于一个2-class分类，取值范围如下：

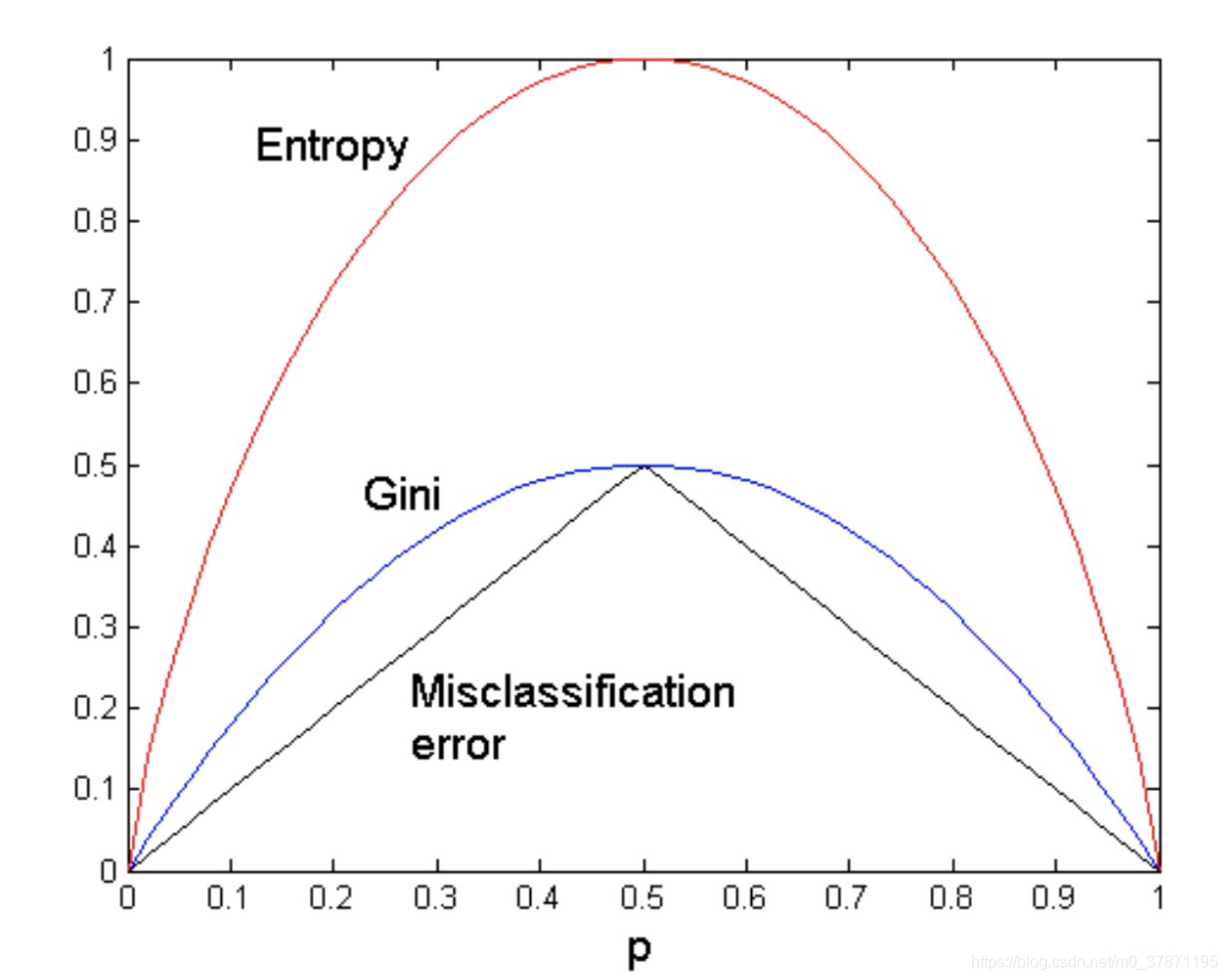
可见在概率等于0.5时，达到峰值，此时纯度最低。而概率越小或越大，确定性就越高，纯度越大。