概率图模型2(马尔科夫网络)

马尔科夫网络属于无向图模型

条件独立性体现在三个方面：
$$条件独立性：\{\begin{array}{l}全局：X_A\perp X_B|X_C\\ 局部：x_i\perp x_{i-nb}|x_{nb}给定x_i的邻居x_{nb}情况下，x_i独立于x_i的非邻居\\ 成对：x_i\perp x_j|x_{-i,j}给定所有非x_i和x_j情况下，x_i独立于x_j\end{array}$$
三个方面可以相互转换

$全局<<==>>局部<<==>>成对$

团和最大团的概念：
团：两两相连的节点叫做团
最大团：不能再添加任何节点的团叫做最大团

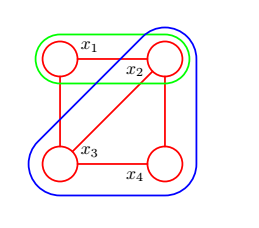
比如上图中$(x_1,x_2),(x_1,x_3)(x_1,x_2,x_3),(x_2,x_3,x_4)$都叫团，其中$(x_1,x_2,x_3),(x_2,x_3,x_4)$
是最大团

接下来我们可以顺利讨论怎么分解因子写出来联合概率了，但是由于公式看着理解比较棘手，我们先看一个具体的例子算式，这样有助于我们理解公式

此图包含三个最大团
$C_1=(x_1,x_2,x_3),C_2=(x_3,x_4),C_3=(x_3,x_5)$

那么此马尔科夫网络的联合概率分布可以写为：
$p(x_1,x_2,x_3,x_4,x_5)=\frac{1}{Z}\psi (X_{C_1})\psi (X_{C_2})\psi (X_{C_3})=\frac{1}{Z}\psi (x_1,x_2,x_3)\psi (x_3,x_4)\psi (x_3,x_5)=\frac{1}{Z}\prod \psi (X_{C_i})$
其中：
$Z=\sum \prod \psi (X_{C_i})=\sum _1\sum _2\sum _3...\sum _p\prod \psi (X_{C_i})叫做归一化因子$
$\psi (X_{C_i})叫做势函数，是指数函数$
ψ ( X C i ) = e x p { − E ( X C i ) } , E 表 示 能 量 函 数 \psi(X_{C_i})=exp\{-E(X_{C_i})\},E表示能量函数 ψ(XCi​​)=exp{−E(XCi​​)},E表示能量函数
比如 ψ ( X C 2 ) = e x p { E ( X C 2 ) } = e x p { − E ( x 3 , x 4 ) } \psi(X_{C_2})=exp\{E(X_{C_2})\}=exp\{-E(x_3,x_4)\} ψ(XC2​​)=exp{E(XC2​​)}=exp{−E(x3​,x4​)}

重写无向图联合概率公式：
$P(X)=\frac{1}{Z}\prod _i^k\psi (X_{C_i})$

而基于最大团的联合概率和无向图的条件独立性等价，这点由Hammersley-Clifford定理保证

因子图
因子图可以看作是对势函数的进一步分解

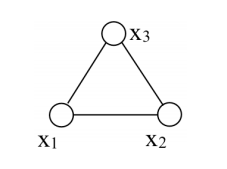
$p(x_1,x_2,x_3)=\psi (x_1,x_2,x_3)$
因子图的表现形式如下：

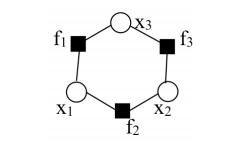
在每个相连的节点间都插入因子节点（函数节点），概率的表现形式如下：
$p(x_1,x_2,x_3)=f_1(x_1,x_3)f_2(x_1,x_2)f_3(x_2,x_3)$