Learning to Rank: From Pairwise Approach to Listwise Approach

解决的问题

关于排序已经有很多方法提出了，它们的共同点就是将object对当做学习的实例，我们把它们叫做pairwise的方法。Pairwise方法有诸多优点，但它们忽略了一个事实——排序是一个在object list上进行预测的任务。本文认为排序应该以一个list的object作为实例。

listwise方法

在本节我们以文档召回为例简短介绍一下learning to rank，再着重介绍listwise方法。下面我们用上标来代表query的index，下标表示doc的index。
在训练过程中，给出一个集合的query Q = { q ( 1 ) , q ( 2 ) , . . . , q ( m ) } Q = \{ q^{(1)}, q^{(2)}, ..., q^{(m)}\} Q={q(1),q(2),...,q(m)}，每个query与一个list的doc $d^{(i)}=(d_1^{(i)},d_2^{(i)},...,d_{n^{(i)}}^{(i)})$相关联。其中$d_j^{(i)}$表示第j个doc，$n^{(i)}$表示$d^{(i)}$的长度。此外，每个doc list的doc $d^{(i)}$与一个list的score $y^{(i)}=(y_1^{(i)},y_2^{(i)},...,y_{n^{(i)}}^{(i)})$相关联。分数表示doc和query间的相关性，可以是用户给出的显式或隐式的分数。
一个特征向量$x_j^{(i)}=\Phi (q^{(i)},d_j^{(i)})$会从每个query-doc对中抽取出来。每个list的特征 $x^{(i)}=(x_1^{(i)},x_2^{(i)},...,x_{n^{(i)}}^{(i)})$就有了相关联的分数$y^{(i)}=(y_1^{(i)},y_2^{(i)},...,y_{n^{(i)}}^{(i)})$。于是训练集就可以表示为 T = { ( x ( i ) , y ( i ) ) } i = 1 m T = \{(x^{(i)}, y^{(i)})\}_{i=1}^m T={(x(i),y(i))}i=1m​。
对于一个list的特征向量$x^{(i)}$，我们的排序模型得到一个list的分数$z^{(i)}=(f(x_1^{(i)}),f(x_2^{(i)}),...,f(x_{n^{(i)}}^{(i)}))$，训练的损失函数为$$\sum _{i=1}^{m}L(y^{(i)},z^{(i)})$$，其中$L$是listwise损失。
在排序过程中，当给出一个新的query和与它关联的一个list的doc，我们就用训练好的排序模型来对它们进行排序。

概率模型

为计算listwise的loss，我们提出了一个概率模型——我们将一个list的score映射为一个概率分布，然后将两个概率分布间的metric作为loss。两个概率模型分别为permutation probability和top one probability。

Permutation Probability

假设将要被排序的ojbects用1,2, …, n来标示。一个permutation （排列）$\pi$定义为{1, 2, …, n}到自身的双射，我们将其写作$\pi =<\pi (1),\pi (2),...,\pi (n)>$，对于所有n个object的可能的排列表示为${\Omega }_n$。
假设我们现在有一个排序函数，为每个object打了一个分数，我们用s来表示分数的list: $s=(s_1,s_2,...,s_n)$。之后我们对排序函数和用排序函数打出的分数会不作区分。
下面我们就可以定义排列概率来表示一个排序函数的似然——
定义1：假设$\pi$是在n个object上的一个排列，$\varphi (.)$是一个单调递增的正函数，那么在给定$s$的情况下，排列$\pi$的概率为：$$P_s(\pi )=\prod _{j=1}^n\frac{\Phi (s_{\pi (j)})}{{\sum }_{k=j}^n\Phi (s_{\pi (k)})}$$
其中$s_{\pi (j)}$是被排在j位置的object的分数。
考虑一个例子，假设3个object {1, 2, 3} 的分数 $s=(s_1,s_2,s_3)$，两个排列$\pi =<1,2,3>$和$\pi =<3,2,1>$的概率分别是：

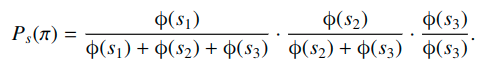
和

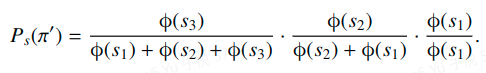
对于以上排列概率我们有一个引理。
引理2：排列概率对于排列的集合服从概率分布，即对于任意排列$\pi \in {\Omega }_n$，有$P_s(\pi )>0和{\sum }_{\pi \in {\Omega }_n}{P}_s(\pi )=1$
定理3: 给定两个排列$\pi$和${\pi }^{\prime }$，若(1) $\pi (p)={\pi }^{\prime }(q),\pi (q)={\pi }^{\prime }(p),p<q$; (2) $\pi (r)={\pi }^{\prime }(r),r\ne p,q$; (3) $s_{\pi (p)}>s_{\pi (q)}$，则$P_s(\pi )>P_s({\pi }^{\prime })$
定理4: 对于n个objects，若$s_1>s_2>...>s_n$，则$P_s(<1,2,...,n>)$是排列概率最大的一个排列，$P_s(<n,n-1,...,1>)$是排列概率最小的一个排列。
定理3表示对于任意排好序的list，如果我们交换一个分数较高和一个分数较低的object的顺序，排列概率就会降低。定理4表示按照分数降序的排列有最高的排列概率，而按分数升序的排列概率最低。
给出两列分数，我们可以先计算出它们的排列概率，然后计算两个分布的距离来作为listwise的loss。由于n个object的排列数量是n!个，全部计算出来是不现实的，我们利用top one概率来解决这个问题。

top one probability

一个object的top one概率代表它被排在top 1的概率。
定义5：object j的top one probability定义为：
$$P_s(j)=\sum _{\pi (1)=j,\pi \in {\Omega }_n}{P}_s(\pi )$$
也就是说，object j的top one概率等于j被排在第一位的所有排列的排列概率之和。对于这一概率我们有更加简便的算法。
定理6：对于top one概率$P_s(j)$，我们有：
$$P_s(j)=\frac{\Phi (s_j)}{{\sum }_{k=1}^n\Phi (s_k)}$$其中$s_j$表示object的分数。
引理7：top one概率在n个object的集合上组成概率分布。
定理8：给出两个ojbect j和k，若$s_j>s_k,j\ne k,k=1,2,...,n$，则$P_s(j)>P_s(k)$
以上所有定理的证明见原文附录。
有了上面的top one概率，给出两列分数我们可以利用任意的度量元来度量两列分数间的距离。例如当用交叉熵作为度量时，listwise loss就会变成：
$$L(y^{(i)},z^{(i)})=-\sum _{j=1}^n{P}_{y^{(i)}}(j)log(p_{z^{(i)}}(j))$$

训练方法：ListNet

本节依旧以文档召回为例。我们将基于神经网络的排序函数表示为$f_{\omega }$，给出一个特征向量$x_j^{(i)}$，$f_{\omega }(x_j^{(i)})$表示它的分数。为简化过程，我们定义1中的$\Phi$为一个指数函数，于是定理6可以写成：
$$P_s(j)=\frac{\Phi (s_j)}{{\sum }_{k=1}^n\Phi (s_k)}=\frac{exp(s_j)}{{\sum }_{k=1}^{n}exp(s_k)}$$
给出query $q^{(i)}$，排序函数$f_{\omega }$能够生成一个分数list $z^{(i)}(f_{\omega })=(f_{\omega }(x_1^{(i)}),f_{\omega }(x_2^{(i)}),...,f_{\omega }(x_{n^{(i)}}^{(i)}))$，若采用交叉熵作为度量，query的loss可以写作：
$$L(y^{(i)},z^{(i)}(f_{\omega }))=-\sum _{j=1}^{n^{(i)}}{P}_{y^{(i)}}(x_j^{(i)})log(P_{z^{(i)}(f_{\omega })}(x_j^{(i)}))$$

读这篇文章的目的是为了读Session-aware Information Embedding for E-commerce ProductRecommendation，所以实验部分有缘再写（。