博客内容将首发在微信公众号"跟我一起读论文啦啦",上面会定期分享机器学习、深度学习、数据挖掘、自然语言处理等高质量论文,欢迎关注!

本篇博文分享和总结下论文 L e a r n i n g t o R a n k : F r o m P a i r w i s e A p p r o a c h t o L i s t w i s e A p p r o a c h Learning\ to\ Rank: From\ Pairwise\ Approach\ to\ Listwise\ Approach Learning to Rank:From Pairwise Approach to Listwise Approach,论文链接listNet,参考的实现代码:实现代码
本篇论文和深度学习关系大,主要是关于排序、推荐、文件检索等方面,因为实习时涉及到一些排序模型,所以在此延伸和总结下。
pairwise优缺点
优点:
- 一些已经被验证的较好的分类模型可以直接拿来用。
- 在一些特定场景下,其 p a i r w i s e f e a t u r e s pairwise\ features pairwise features 很容易就可以获得。
缺点:
- 其学习的目标是最小化文档对的分类错误,而不是最小化文档排序的错误。学习目标和实际目标( M A E , N D C G MAE, NDCG MAE,NDCG)有所违背。
- 训练过程可能是极其耗时的,因为生成的文档对样本数量可能会非常多。
那么本篇论文是如何解决这些问题呢?
- 在 p o i n t w i s e pointwise pointwise 中,我们将每一个 < q u e r y , d o c u m e n t > <query, document> <query,document> 作为一个训练样本来训练一个分类模型。这种方法没有考虑文档之间的顺序关系;而在 p a r i w i s e pariwise pariwise 方法中考虑了同一个 q u e r y query query 下的任意两个文档的相关性,但同样有上面已经讲过的缺点;在 l i s t w i s e listwise listwise 中,我们将一个 < q u e r y , d o c u m e n t s > <query, documents> <query,documents> 作为一个样本来训练,其中** d o c u m e n t s documents documents 为与这个 q u e r y query query 相关的文件列表**。
- 论文中还提出了概率分布的方法来计算 l i s t w i s e listwise listwise 的损失函数。并提出了 p e r m u t a t i o n p r o b a b i l i t y permutation\ probability permutation probability 和 t o p o n e p r o b a b i l i t y top\ one\ probability top one probability 两种方法。下面会详述这两种方法。
Listwise Approach
假设我们有
m
m
m 个
q
u
e
r
y
s
querys
querys:
Q
=
(
q
(
1
)
,
q
(
2
)
,
q
(
3
)
,
.
.
.
,
q
(
m
)
)
Q=(q^{(1)}, q^{(2)}, q^{(3)},...,q^{(m)})
Q=(q(1),q(2),q(3),...,q(m))
每个
q
u
e
r
y
query
query 下面有
n
n
n 个可能与之相关的文档(对于不同的
q
u
e
r
y
query
query ,其
n
n
n 可能不同):
d
(
i
)
=
(
d
1
(
i
)
,
d
2
(
i
)
,
.
.
.
,
d
n
(
i
)
)
d^{(i)} = (d^{(i)}_1, d^{(i)}_2, ..., d^{(i)}_n)
d(i)=(d1(i),d2(i),...,dn(i))
对于每个
q
u
e
r
y
query
query 下的所有文档,我们可以根据具体的应用场景得到每个文档与
q
u
e
r
y
query
query 的真实相关度得分。
y
(
i
)
=
(
y
1
(
i
)
,
y
2
(
i
)
,
.
.
.
.
,
y
n
(
i
)
)
y^{(i)} = (y^{(i)}_1, y^{(i)}_2, ...., y^{(i)}_n)
y(i)=(y1(i),y2(i),....,yn(i))
我们可以从每一个文档对
(
q
(
i
)
,
d
j
(
i
)
)
(q^{(i)}, d^{(i)}_{j})
(q(i),dj(i)) 得到该文档的特征向量,由此可以得到该
q
u
e
r
y
query
query 下的所有文档的特征向量:
x
(
i
)
=
(
x
1
(
i
)
,
x
2
(
i
)
,
.
.
.
,
x
n
(
i
)
)
x^{(i)} = (x^{(i)}_1, x^{(i)}_2, ..., x^{(i)}_n)
x(i)=(x1(i),x2(i),...,xn(i))
并且可知每个文档真实相关度得分:
y
(
i
)
=
(
y
1
(
i
)
,
y
2
(
i
)
,
.
.
.
,
y
n
(
i
)
)
y^{(i)}= (y^{(i)}_1, y^{(i)}_2, ... , y^{(i)}_n)
y(i)=(y1(i),y2(i),...,yn(i))
由此,我们可以构建训练样本:
T
=
{
(
x
(
i
)
,
y
(
i
)
)
}
i
=
1
m
\ T = \begin{Bmatrix} (x^{(i)}, y^{(i)}) \end{Bmatrix}_{i=1}^m
T={(x(i),y(i))}i=1m
要特别注意的是:这里面一个训练样本是 ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i)),而这里的 x ( i ) x^{(i)} x(i) 是一个与 q u e r y query query 相关的文档列表,这也是区别于 p o i n t w i s e pointwise pointwise 和 p a i r w i s e pairwise pairwise 的一个重要特征。
那么有训练样本了,如何计算
l
o
s
s
loss
loss 呢?
假设我们已经有了排序函数
f
f
f,我们可以计算特征向量
x
(
i
)
x^{(i)}
x(i) 的得分情况:
z
(
i
)
=
(
f
(
x
1
(
i
)
)
,
f
(
x
2
(
i
)
)
,
.
.
.
,
f
(
x
n
(
i
)
)
)
z^{(i)} = (f(x_1^{(i)}), f(x_2^{(i)}), ..., f(x_n^{(i)}))
z(i)=(f(x1(i)),f(x2(i)),...,f(xn(i)))
显然我们学习的目标就是,最小化真实得分和预测得分的误差:
∑
i
=
1
m
L
(
y
(
i
)
,
z
(
i
)
)
\sum_{i=1}^{m} L(y^{(i)}, z^{(i)})
i=1∑mL(y(i),z(i))
L
L
L 为
l
i
s
t
w
i
s
e
listwise
listwise 的损失函数。
概率模型
假设对于某一个
q
u
e
r
y
query
query 而言,与之可能相关的文档有
{
1
,
2
,
3
,
.
.
.
,
n
}
\{1, 2, 3, ..., n\}
{1,2,3,...,n},假设某一种排序的结果为
π
\pi
π:
π
=
<
π
(
1
)
,
π
(
2
)
,
.
.
,
π
(
n
)
>
\pi=<\pi(1), \pi(2), .., \pi(n)>
π=<π(1),π(2),..,π(n)>
另外一种排序结果为
π
′
{\pi}'
π′:
π
′
=
<
π
′
(
n
)
,
π
′
(
n
−
1
)
,
.
.
,
π
′
(
1
)
>
{\pi}'=<{\pi}'(n), {\pi}'(n-1), .., {\pi}'(1)>
π′=<π′(n),π′(n−1),..,π′(1)>
对于 n n n 个文档,有 n ! n! n! 种排列情况。这所有的排序情况记为 Ω n \Omega_n Ωn。假设已有排序函数,那么对于每个文档,我们都可以计算出相关性得分 s = ( s 1 , s 2 , . . . , s n ) s = (s_1, s_2, ..., s_n) s=(s1,s2,...,sn)。
显然对于每一种排序情况,都是有可能发生的,但是每一种排列都有其最大似然值。
我们可以这样定义某一种排列
π
\pi
π 的概率(最大似然值):
P
s
(
π
)
=
∏
j
=
1
n
ϕ
(
s
π
(
j
)
)
∑
k
=
j
n
ϕ
(
s
π
(
k
)
)
P_s(\pi) = \prod_{j=1}^{n} \frac{\phi (s_{\pi(j)})}{\sum_{k=j}^{n}\phi(s_{\pi(k)})}
Ps(π)=j=1∏n∑k=jnϕ(sπ(k))ϕ(sπ(j))
例如有三个文档 p i = < 1 , 2 , 3 > \ pi = <1,2,3> pi=<1,2,3> ,其排序函数计算每个文档得分为 s = ( s 1 , s 2 , s 3 ) s=(s_1, s_2, s_3) s=(s1,s2,s3),则该种排序概率为:

对于另外一种排序,例如 π ′ = < 3 , 2 , 1 > {\pi}' = <3,2,1> π′=<3,2,1> ,则这种排列概率为:

论文中总结了一些排序的性质,但是我感觉没什么卵用。
Top K Probability
上面那种计算排列概率的方式,其计算复杂度达到 n ! n! n!,太耗时间,由此论文中提出了一种更有效率的方法 t o p o n e top\ one top one。我们在这里推广到 t o p k topk topk 来分析总结。
上面计算某一种排序方式概率:
P
s
(
π
)
=
∏
j
=
1
n
ϕ
(
s
π
(
j
)
)
∑
k
=
j
n
ϕ
(
s
π
(
k
)
)
P_s(\pi) = \prod_{j=1}^{n} \frac{\phi (s_{\pi(j)})}{\sum_{k=j}^{n}\phi(s_{\pi(k)})}
Ps(π)=j=1∏n∑k=jnϕ(sπ(k))ϕ(sπ(j))
排在第一位的有
n
n
n 种情况,排在第二位的有
n
−
1
n-1
n−1 种情况,后面依次类推。相当与利用
t
o
p
n
top\ n
top n 来计算。
那么
t
o
p
K
(
K
<
n
)
top\ K(K<n)
top K(K<n) 计算:
P
s
(
π
)
=
∏
j
=
1
K
ϕ
(
s
π
(
j
)
)
∑
k
=
j
n
ϕ
(
s
π
(
k
)
)
P_s(\pi) = \prod_{j=1}^{K} \frac{\phi (s_{\pi(j)})}{\sum_{k=j}^{n}\phi(s_{\pi(k)})}
Ps(π)=j=1∏K∑k=jnϕ(sπ(k))ϕ(sπ(j))
同理,这里的计算复杂度为
n
∗
(
n
−
1
)
∗
(
n
−
2
)
∗
.
.
.
∗
(
n
−
k
+
1
)
n*(n-1)*(n-2)*...*(n-k+1)
n∗(n−1)∗(n−2)∗...∗(n−k+1),即为
N
!
/
(
N
−
k
)
!
N!/(N-k)!
N!/(N−k)! 种不同排列,大大减少了计算复杂度。
如果
K
=
1
K=1
K=1 ,就蜕变成论文中
t
o
p
o
n
e
top\ one
top one 的情况,此时有
n
n
n 种不同排列情况:
P
s
(
π
)
=
ϕ
(
s
π
(
j
)
)
∑
k
=
j
n
ϕ
(
s
π
(
k
)
)
P_s(\pi) = \frac{\phi (s_{\pi(j)})}{\sum_{k=j}^{n}\phi(s_{\pi(k)})}
Ps(π)=∑k=jnϕ(sπ(k))ϕ(sπ(j))
对于 N ! / ( N − k ) ! N!/(N-k)! N!/(N−k)! 种不同的排列情况,就有 N ! / ( N − k ) ! N!/(N-k)! N!/(N−k)! 个排列预测概率,就形成了一种概率分布,再由真实的相关性得分计算相应的排列概率,得到真实的排列概率分布。由此可以利用 c r o s s − e n t r o p y cross-entropy cross−entropy 来计算两种分布的距离作为损失函数:

例如一个查询下有三个文档
<
A
,
B
,
C
>
<A,B,C>
<A,B,C> :
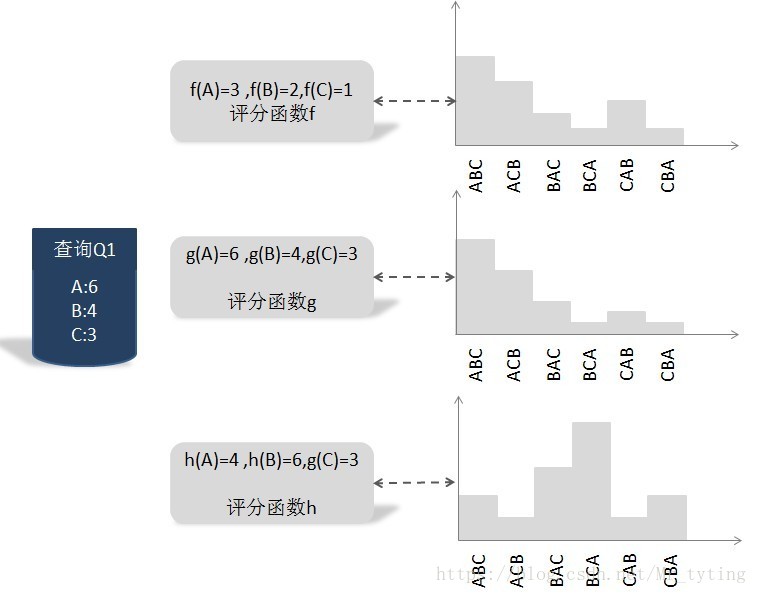
上图中 g g g 为有真实打分计算出的各种排列的概率分布, f 、 h f、h f、h 为另外两种排列概率分布,我们就是需要比较那种排列概率分布与真实的排列概率分布更为接近,就用该分布的预测相关性得分作为最终得分。
ListNet
在论文中, L i s t n e t Listnet Listnet 只是将上面的 t o p K topK topK 中的 ϕ \phi ϕ 函数变成 e x p exp exp 函数:
P s ( π ) = exp ( s π ( j ) ) ∑ k = j n exp ( s π ( k ) ) P_s(\pi) = \frac{\exp (s_{\pi(j)})}{\sum_{k=j}^{n}\exp(s_{\pi(k)})} Ps(π)=∑k=jnexp(sπ(k))exp(sπ(j))
这样不就是计算预测出的得分的 s o f t m a x softmax softmax 了吗?实际上的确如此,在实现代码中就是这样做的,当时我直接看代码还一脸懵逼,这不就是对文档预测出来的得分做了个 s o f t m a x softmax softmax 操作吗?跟 t o p − o n e top-one top−one 有什么关系,仔细看论文才知道怎么回事。
t o p − o n e top-one top−one 时,只有 n n n 种排列情况,这大大减少了计算量。如果 t o p K ( K > 1 ) topK (K>1) topK(K>1) ,则需要计算的排列情况就会变多。
假设排序函数 f f f 的参数为 w w w ,则 t o p − o n e top-one top−one 的排列概率分布为:
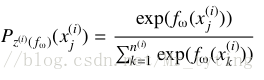
算法流程:

这里还是需要注意:是将某一个查询下的所有可能与之相关的文档列表,作为一个样本来训练。
损失函数:

参数求导:

以上就是 L i s t N e t ListNet ListNet 的大体思路。
我们找出了这样排序函数 f w f_w fw 后,然后利用其给文档的打分,来给文档进行排序。
个人总结
- 在 p a i r w i s e pairwise pairwise 中,只考虑了两个文档对的相对先后顺序,却没有考虑文档出现在搜索列表中的位置,排在搜索站果前列的文档更为重要,如果前列文档出现判断错误,代价明显高于排在后面的文档。针对这个问题的改进思路是引入代价敏感因素,即每个文档对根据其在列表中的顺序具有不同的权重,越是排在前列的权重越大,即在搜索列表前列,如果排错顺序的话其付出的代价更高(评价指标NDCG); 而 l i s t w i s e listwise listwise 讲一个查询下的所有文档作为一个样本,因为要组合出不同的排列,得到其排列概率分布,来最小化与真实概率分布的误差,这里面就考虑了文档之间的各种顺序关系。很好的避免了这种情况。
- 从概率模型的角度定义损失函数。
- 在实做时,其实将一个 q u e r y query query 下的的所有可能与之相关的 n 个 d o c n\ 个doc n 个doc 作为一个训练样本(这时可以理解 b a t c h _ s i z e = n batch\_size = n batch_size=n) ,一定要注意:在计算 t o p _ o n e p r o b a b i l i t y top\_one\ probability top_one probability 时,是在一个 q u e r y query query 内的所有文档做 s o f t m a x softmax softmax ,而不是在当前正在训练的所有的样本内做。这是区别 p o i n t w i s e 、 p a i r w i s e pointwise、pairwise pointwise、pairwise 的重要不同之处。


























 254
254

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








