（四）最邻近插值、双线性插值

最新推荐文章于 2024-04-20 22:11:14 发布

淡定的炮仗

最新推荐文章于 2024-04-20 22:11:14 发布

阅读量7.1k

点赞数 13

分类专栏：数字图像处理入门文章标签：数字图像处理计算机视觉

本文链接：https://blog.csdn.net/m0_43609475/article/details/111648280

版权

数字图像处理入门专栏收录该内容

24 篇文章

订阅专栏

本文详细介绍了图像放大和缩小的基本原理——映射，并探讨了两种常见的插值方法：最邻近插值和双线性插值。最邻近插值通过选取最接近的像素值来处理小数坐标，可能导致图像边缘锯齿状。而双线性插值则利用四个相邻像素的加权平均，提供更平滑的图像过渡。文章还提供了Python代码实现这两种插值算法，以实际图像为例展示了放大效果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最邻近插值、双线性插值、三线性插值

零、图像的放大和缩小的基本原理–映射

图像的放大和缩小的基本原理就是一种映射，即缩小后或者放大后的图像像素位置向原图的一个映射。简单理解就是，将放大或者缩小后的图像将其的坐标（长宽）拉伸或者压缩到和原图一样大时，其像素坐标点对应在原图上的位置就是其映射位置

坐标映射图

一、插值法放缩放图像算法第一步映射

1. 值法算法流程----映射：
(1)、插值法放大图像的第一步都是相同的，遍历新图。计算新图的坐标点像素值对应原图中哪个坐标点的像素值来填充，计算公式为：
对应成比例scrH/dstH = srcHeight/dstHeight >>>
scrH = dstH * (srcHeight/dstHeight)
对应成比例scrW/dstW = srcWidth/dstWidth >>>
scrW = dstW * (srcWidth/dstWidth)
其中，src表示旧图，dst表示新图。新图的坐标（dstH,dstW）对应于旧图的坐标（scrH,scrW）。
srcWidth/dstWidth 和 srcHeight/dstHeight 分别表示宽和高的放缩比。

2、总结
那么问题来了，通过这个映射公式算出来的 scrH,scrW（旧图坐标）有可能是小数，但是坐标点是不存在小数的，都是整数，得想办法把它转换成整数才行。
不同插值法的区别就体现在 scrH,scrW 是小数时，怎么变成整数----去取原图像中的像素值。
最近邻插值（Nearest-neighborInterpolation）： 看名字就很直白，四舍五入选取最接近的整数。这样的做法会导致像素变化不连续，在目标图像中产生锯齿边缘。
双线性插值（Bilinear Interpolation）： 双线性就是利用与坐标轴平行的两条直线去把小数坐标分解到相邻的四个整数坐标点。权重与距离成反比。
双三次插值（Bicubic Interpolation）： 与双线性插值类似，只不过用了相邻的16个点。但是需要注意的是，前面两种方法能保证两个方向的坐标权重和为1，但是双三次插值不能保证这点，所以可能出现像素值越界的情况，需要截断。

二、最邻近插值法：

最邻近插值法： 看名字就很直白，将scrH,scrW ，四舍五入选取最接近的整数，得到该点的像素值（该整数坐标在原图上的像素值）。这样的做法会导致像素的变化不连续，在新图中会产生锯齿。

四、python实现最邻近插值算法

import cv2
import numpy as np
scr_img = cv2.imread("lenna.png", 1)
print(scr_img.shape)
cv2.imshow("scr_img", scr_img)
cv2.waitKey(0)
# print(scr_img[0][0])
def nearest_neighbor_interpolation(scr_img,dstHeight,dstWidth):
    if(len(scr_img.shape)>2):# 图像不是灰度图像
        srcHeight, srcWidth, channels = scr_img.shape  # 获取原图的形状
        # 创建新图
        dst_img = np.zeros((dstHeight,dstWidth,channels),dtype = np.uint8)
        # 遍历新图,计算新图像素坐标在原图上的映射坐标
        for dstH in range(dstHeight):
            for dstW in range(dstWidth):
                scrH = round((dstH)*(srcHeight/dstHeight))
                scrW = round((dstW)*(srcWidth/dstWidth))
                dst_img[dstH][dstW] = scr_img[scrH][scrW]
        return  dst_img
    else:#图像是灰度图像
        srcHeight, srcWidth = scr_img.shape  # 获取原图的形状
        dst_img = np.zeros((dstHeight, dstWidth), dtype=np.uint8)
        # 遍历新图,计算新图像素坐标在原图上的映射坐标
        for dstH in range(dstHeight):
            for dstW in range(dstWidth):
                scrH = round((dstH) * (srcHeight / dstHeight))
                scrW = round((dstW) * (srcWidth / dstWidth))
                dst_img[dstH][dstW] = scr_img[scrH][scrW]
        return dst_img
dstHeight,dstWidth = 1000,1000
dst_img = nearest_neighbor_interpolation(scr_img,dstHeight,dstWidth)
cv2.imshow("dst_img",dst_img)
cv2.waitKey(0)

原图
在这里插入图片描述

放大图
在这里插入图片描述

五、双线性插值法：

1、插值介绍

在离散数据的基础上补插连续函数，使得这条连续曲线通过全部给定的离散数据点。
插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。
插值： 用来填充图像变换时像素之间的空隙。

2、线性插值

线性插值 是指插值函数为一次多项式的插值方式，其在插值节点上的插值误差为零。线性插值相比其他插值方式，如抛物线插值，具有简单、方便的特点。线性插值的几何意义即为概述图中利用过A点和B点的直线来近似表示原函数。线性插值可以用来近似代替原函数，也可以用来计算得到查表过程中表中没有的数值。

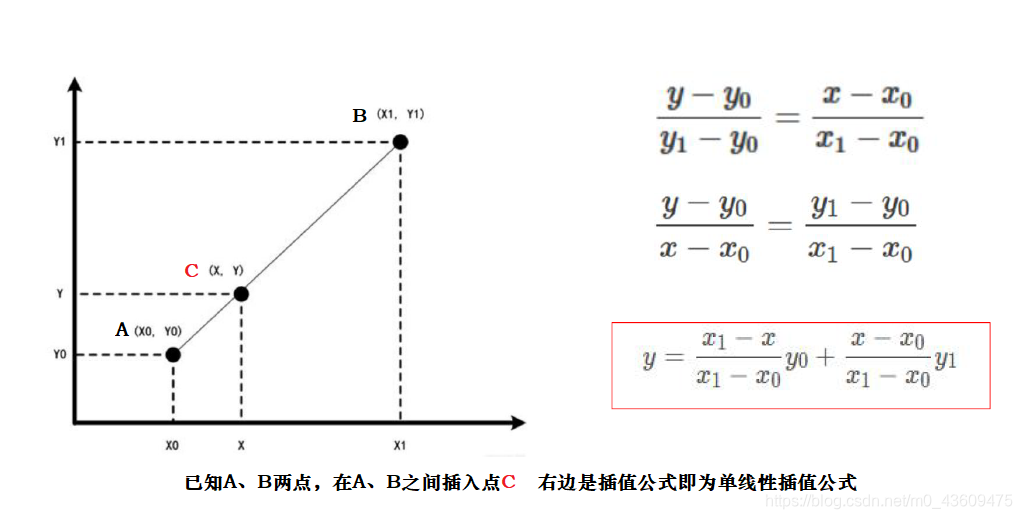
在这里插入图片描述

3、双线性插值

双线性插值就是在x和y方向个来一次单线性插值

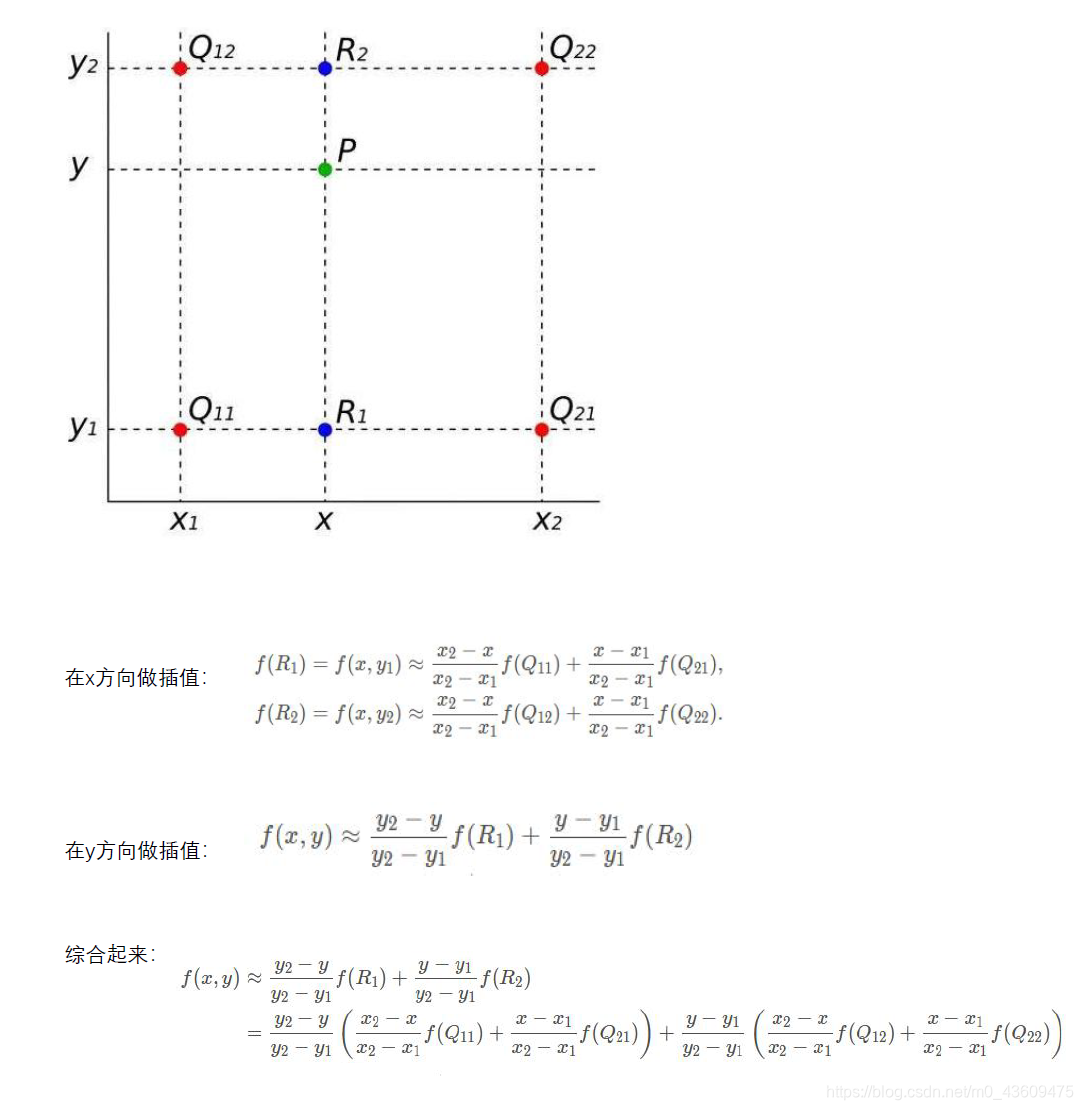
在这里插入图片描述
在图像中 y2-y1=1;x2-x1=1（x1 x2 y1 y2 是原图坐标）

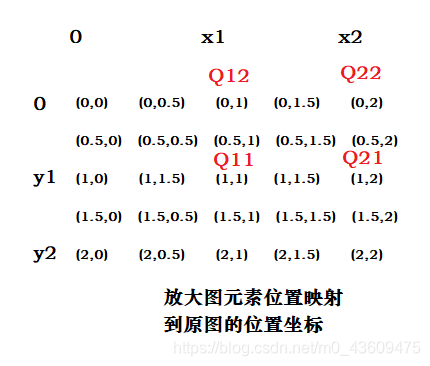
所以上式变为
在这里插入图片描述

在实际图像双线性插值时，即可算出双线性插值的值
在这里插入图片描述

六、python实现双线性插值法：

import cv2
import numpy as np
import math
def bilinear_interpolation(scr_img,dstHeight,dstWidth):
    if(len(scr_img.shape)>2):# 图像是RGB图像
        srcHeight, srcWidth, channels = scr_img.shape  # 获取原图的形状
        scr_img = np.pad(scr_img, ((0, 1), (0, 1), (0, 0)), 'constant')
        # 创建新图
        dst_img = np.zeros((dstHeight,dstWidth,channels),dtype = np.uint8)
        # 遍历新图,计算新图像素坐标在原图上的映射坐标
        for dstH in range(dstHeight):
            for dstW in range(dstWidth):
                scrH = (dstH)*(srcHeight/dstHeight)
                scrW = (dstW)*(srcWidth/dstWidth)
                # i,j = int(scrH),int(scrW)  # 获得映射到原图的位置的左上角的像素位置
                i,j = math.floor(scrH),math.floor(scrW)  # 获得映射到原图的位置的左上角的像素位置
                u,v = scrH-i,scrW-j  # 获得映射到原图的位置的到左上角的像素位置的距离 x距离和y距离
                dst_img[dstH][dstW] = (1-u)*(1-v)*scr_img[i][j] + (1-u)*v*scr_img[i][j+1] + u*(1-v)*scr_img[i+1][j] + u*v*scr_img[i+1][j+1]
        return  dst_img
    else:#图像是灰度图像
        srcHeight, srcWidth = scr_img.shape  # 获取原图的形状
        dst_img = np.zeros((dstHeight, dstWidth), dtype=np.uint8)
        # 遍历新图,计算新图像素坐标在原图上的映射坐标
        for dstH in range(dstHeight - 1):
            for dstW in range(dstWidth - 1):
                scrH = (dstH+0.5) * (srcHeight / dstHeight)-0.5
                scrW = (dstW+0.5) * (srcWidth / dstWidth)-0.5
                i, j = int(scrH), int(scrW)  # 获得映射到原图的位置的左上角的像素位置
                u, v = scrH - i, scrW - j  # 获得映射到原图的位置的到左上角的像素位置的距离 x距离和y距离
                dst_img[dstH][dstW] = (1 - u) * (1 - v) * scr_img[i][j] + (1 - u) * v * scr_img[i][j + 1] + u * (
                            1 - v) * scr_img[i + 1][j] + u * v * scr_img[i + 1][j + 1]
        return dst_img

dstHeight,dstWidth = 500*2,500*2
dst_img = bilinear_interpolation(scr_img,dstHeight,dstWidth)
cv2.imshow("dst_img",dst_img)
cv2.waitKey(0)