1. k k k-NN
k k k-NN 是一种基本的监督学习方法,它和感知机有些不同。具体地,它没有一个明确策略,也就是没有损失函数,因此它没有一个显式的学习过程。
1.1 模型概述
k
k
k-NN 的思想大概类似于 近朱者赤,近墨者黑。也就是说一个样本的邻居大多属于哪一类,那么这个样本也就是属于那一类。
k
k
k-NN 的模型实际上也就是对应于特征空间的划分。
显然划分特征空间需要仔细定义以下问题:
- k k k 值的选择: 也就是说选择多少个邻居作为评判的依据
- 距离度量: 越近的邻居和该样本点越相似,我们应该如何度量邻居之间距离的远近
- 分类决策规则: 已经选出了具体的邻居,应该如何根据邻居来确定该样本的类别
以上就是 k k k-NN 模型的三个基本要素,确定了这 3 3 3 个要素,就是确定了 k k k-NN 模型。
1.1.1 k k k 值的选择
k k k 值实际上是一个超参数,也就是说这并不是由算法通过学习而确定值的一个参数,而是需要人为提前指定值的一个参数。 k k k 值作为该算法模型的三要素之一,对算法的行为影响巨大,通常来说, k k k 值应该取一个 较小 的值,且一般通过 交叉验证法 来选取。
-
k
k
k 值太大
- 意味着整体模型变 简单,忽略了较多有用信息
- 可以减少学习的估计误差,但会增大学习的近似误差
-
k
k
k 值太小
- 意味着模型变 复杂,容易过拟合
- 近似误差会减小
1.1.2 距离度量
k k k-NN 常使用的是 欧氏距离 Euclidean distance,列举出几种常见的距离如下。
-
L
p
L_p
Lp 距离:
p
≥
1
p\geq 1
p≥1
L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ p ) 1 p L_p(x_i,x_j)=(\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|^p)^{\frac{1}{p}} Lp(xi,xj)=(l=1∑n∣xi(l)−xj(l)∣p)p1
下面列举的几种距离都是当 p p p 取某特定值时的 L p L_p Lp 距离
- 欧氏距离 Euclidean distance:
p
=
2
p=2
p=2
L 2 ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ 2 ) 1 2 L_2(x_i,x_j)=(\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|^2)^{\frac{1}{2}} L2(xi,xj)=(l=1∑n∣xi(l)−xj(l)∣2)21 - 曼哈顿距离 Manhattan distance:
p
=
1
p=1
p=1
L 1 ( x i , x j ) = ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ L_1(x_i,x_j)=\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}| L1(xi,xj)=l=1∑n∣xi(l)−xj(l)∣ -
p
=
∞
p=\infty
p=∞
L ∞ ( x i , x j ) = max l ∣ x i ( l ) − x j ( l ) ∣ L_\infty(x_i,x_j)=\max_l|x_i^{(l)}-x_j^{(l)}| L∞(xi,xj)=lmax∣xi(l)−xj(l)∣
1.1.3 分类决策规则
通常来说
k
k
k-NN 的分类决策规则是 投票表决,也就是说,在选定的邻居中,哪一类最多,就将该样本点归于那一类。
max
∑
x
i
∈
N
k
(
x
)
I
(
y
i
=
c
j
)
\max\sum_{x_i\in N_k(x)}I(y_i=cj)
maxxi∈Nk(x)∑I(yi=cj)
也就是如上述公式所表达的意思。
1.2 算法
k
k
k-NN 没有策略,同时它的算法也和感知机不同。感知机的算法是依据策略 (损失函数) 求取模型
y
=
w
⋅
x
+
b
y=w\cdot x+b
y=w⋅x+b 中的最优参数
w
w
w 和
b
b
b。但
k
k
k-NN 的算法并不用来求取任何参数,而是使用模型的三要素来构建分类的流程。
具体的判定一个样本类别的算法流程如下:
- 根据指定的距离度量,选取 k k k 个最近邻
- 求出 k k k 个最近邻中数量最多的那个类别,做该样本的类别
2. 实现 k k k-NN
实现 k k k-NN 代码时,依然按照 感知机 的类架构来设计类。即包含以下三个主体和一些辅助函数。
- __init__()
- fit()
- predict()
2.1 代码实现
具体代码如下
import numpy as np
class KNN:
"""k 近邻法 k-nearest neighbor"""
def __init__(self, k=1, dist_measure="L2"):
"""
成员变量: 即超参数
Args:
k(int): 选定的邻居数量
dist_measure(string): 距离度量方式
"""
self.k = k
if dist_measure == "L2":
self.dist_measure = lambda x, y: np.linalg.norm(x - y)
else:
self.dist_measure = dist_measure
def fit(self, X, Y):
"""
训练方法: k-NN 没有显式的训练过程, 所以这里只是接收训练数据
Args:
X(ndarray): 训练数据的特征矩阵
Y(ndarray): 训练数据的真实类别向量
"""
self.X = X
self.Y = Y
self.k = min(self.k, len(X)) # 邻居数量不能超过训练数据的数量
def predict(self, X):
"""
预测方法: 根据训练好的模型,预测测试数据的类别
Args:
X(ndarray): 测试数据的属性矩阵
Returns:
所有测试数据预测类别组成的向量
"""
return apply_along_axis(self._predict, axis=-1, arr=X)
def _predict(self, x):
"""
辅助方法: 使用当前模型,预测某一数据 x 的类别 y
Args:
x(ndarray): 一条数据的属性向量
Returns:
预测结果,即类别 y
"""
# 1. 确定 k 近邻, 获取它们的下标
topk_idx = self._knn(x)
# 2. 根据下标获取它们的类别
topk_y = self.Y[topk_idx]
# 3. 选择数量最多的类别返回
return np.argmax(np.bincount(topk_y))
def _knn(self, x):
"""
辅助方法: 在训练数据 X 中寻找测试数据 x 的 k 个最近邻,返回它们的下标
Args:
x(ndarray): 一条数据的属性向量
Returns:
在训练数据中与测试数据 x 最近的 k 条数据的下标
"""
# 1. 计算测试数据和每条训练数据之间的距离
dist = np.apply_along_axis(partial(self.dist_measure, y=x), axis=-1, arr=self.X)
# 2. 返回距离最小的 k 个邻居的下标
return np.argpartition(dist, self.k)[:self.k]
2.2 代码中的语法和 API
2.2.1 lambda 匿名函数
lambda 是 Python 中的一个关键字,作用是创建 匿名函数,它的功能要比 def 关键字弱得多,其定义体只能使用 纯表达式,也就是说不可以用 while 和 try 等语句,也不能赋值,因此它的应用场景也非常有限。
- lambda 的使用场景
- 在参数列表中使用,作为参数传递给其他高阶函数
- 其他场景不建议使用 lambda
- lambda 的语法
- 以 lambda 关键开头
- 其后跟参数 (不用加括号,可以有多个)
- 参数后跟英文冒号
- 冒号后是函数体,只能是存表达式
- 示例
# 1. lambda 表达式创建了一个匿名函数,将这个匿名函数赋值给 b
b = lambda x, y: x + y
# 2. 调用 b,即执行了此参数
print(b(5, 6)) # 打印结果是 11
2.2.2 functools.partial 冻结参数
functools.partial 是 Python 中的一个高阶函数,其作用是基于一个函数,将它的某些值固定,而形成一个新的可调用对象。下面给出一个示例
# 从模块 functools 中导入 partial
from functools import partial
# 建立一个简单的函数
def add(a, b):
return a + b
# 用 partial 将 a 的值固定为 7 形成一个新函数 p_add
p_add = partial(add, a=7)
# 调用函数 p_add 时只需要给出参数 b 的值即可
c = p_add(b=4)
print(c) # 打印结果是 11, 相当于 add(7, 4)
需要注意以下几点
- functools.partial: 第一个参数是它基于的函数,后面的参数是原函数中要固定的参数
- 固定参数若给出参数名,则固定对应名字的参数,若不给参数名,则根据基础函数的参数列表从前往后按顺序固定参数
- 调用 偏函数 (由 functools.partial 冻结形成的函数 ) 时,最好给出参数名来赋值,否则它会按基础函数的参数列表顺序进行赋值。如果赋值到了已经冻结的参数上,就会出现错误
2.2.3 numpy 中的 API
注意: 这些 API 的参数列表中有很多参数,我并没有全部列出来,很多参数用默认的就可以了,此处只列出需要常用的需要自己更改的参数。
- np.linalg.norm(x, ord):
- x: 一个 ndarray 数组,当然也可以是一维向量
- ord: 指定范数类型,默认值为
L
2
L_2
L2 范数
- ord=1: L 1 L_1 L1 范数
- ord=2: L 2 L_2 L2 范数
- ord=np.inf: L ∞ L_\infty L∞ 范数
- 作用: 对 ndarray 数组求 ord 范数
# 来看看这一行代码
self.dist_measure = lambda x, y: np.linalg.norm(x-y)
"""
1. lambda 代表此处创建了一个匿名函数,该匿名函数有参数 x, y,可以通过 self.dist_measure(x, y) 来调用
2. 函数体为 np.linalg.norm(x, y)
- x, y 为两个特征向量
- 二者之差的 L2 范数就是二者之间的欧氏距离
3. 对于 ndarray 类型的数组,- 号意味着对应位置相减
"""
- np.bincount(x):
- x: 一个 ndarray 数组,当然也可以是一维向量,里面都是 自然数,即大于等于 0 0 0 的整数
- 作用: 返回一个一维的 ndarray 向量
- 记向量 x 中出现的最大值为 M
- np.bincount(x) 返回的向量一共含有 M + 1 个元素
- 第 i 个值为数 i 在向量 np.bincount(x) 中出现的次数
- 显然,当给出的向量为各个数据点的类别时,该函数有助于我们迅速的找到哪个类别是最多的
- np.argmax(a):
- a: 一个向量,或矩阵,若对矩阵使用,需要指定 axis
- 作用: 返回所给向量中,最大值所在的索引
- 显然它和 np.bincount(x) 合作,可以解决找出哪一类是大多数这一问题
- np.argpartition(a, kth):
- a: 一个向量
- kth: 一个整数
- 作用: 返回一个向量
- 向量中的值代表的是 a 中值的下标
- 在返回的向量中,a 中前 kth 个小元素的下标被排列在最前面
- 该函数有助于在计算出所有距离后,寻找距离最近的 k k k 个邻居的下标
2.2.4 ndarray 数组
对 ndarray 数组,我们可以通过传入一个列表的方式,快速的获取其中的部分元素。
import numpy as np
# 1. 创建一个 numpy 数组
a = np.array([2, 3, 2, 7, 9, 6, 4, 3, 6])
# 2. 创建一个列表,其中的值代表我们要在 a 中取出值的下标
idx = [3, 7, 5, 2]
# 3. 从 a 中取出值
b = a[idx]
b # b 的内容是 [7, 3, 6, 2]
3. k k k-NN 的优化: kd 树
k k k-NN 算法没有显式的学习过程,限制算法时间性能的部分是 寻找 k k k 个最近邻。先回顾一下前面我们是怎么寻找 k k k 近邻的
- 计算测试数据与每个训练数据之间的距离,时间花费 O ( N ) O(N) O(N)
- 从这些距离中,找出 k k k 个距离最小的数据点,返回其下标,时间花费 O ( k N ) O(kN) O(kN)
那么,有没有别的方法,可以降低寻找 k k k 近邻的时间复杂度呢?答案就是 kd 树。
3.1 kd 树简介
kd 树是一种数据结构,其实它就是一棵二叉树,只不过和普通二叉树不同,它的结点中存储的并不是一个单一的值,而是一条数据的 特征向量。在每一层,会选择一个特征作为划分依据,所有的数据依这个特征的值划分成三个部分,挑选该特征为中位数的数据成为根结点,该特征比根结点小的用于构建左子树,比根结点大的用于构建右子树。
3.1.1 构造 kd 树
3.1.1.1 例子
首先给出一个例子,有下列数据集,用它来构造一棵平衡 kd 树
T
=
{
(
2
,
3
)
⊤
,
(
5
,
4
)
⊤
,
(
9
,
6
)
⊤
,
(
4
,
7
)
⊤
,
(
8
,
1
)
⊤
,
(
7
,
2
)
⊤
}
T=\{(2,3)^{\top},(5,4)^{\top},(9,6)^{\top},(4,7)^{\top},(8,1)^{\top},(7,2)^{\top}\}
T={(2,3)⊤,(5,4)⊤,(9,6)⊤,(4,7)⊤,(8,1)⊤,(7,2)⊤}
开始构造:
-
选择第一个特征将所有数据集排序如下:
- T = { ( 2 , 3 ) ⊤ , ( 4 , 7 ) ⊤ , ( 5 , 4 ) ⊤ , ( 7 , 2 ) ⊤ , ( 8 , 1 ) ⊤ , ( 9 , 6 ) ⊤ } T=\{(2,3)^{\top},(4,7)^{\top},(5,4)^{\top},(7,2)^{\top},(8,1)^{\top},(9,6)^{\top}\} T={(2,3)⊤,(4,7)⊤,(5,4)⊤,(7,2)⊤,(8,1)⊤,(9,6)⊤},中位数是 7 7 7,选择 ( 7 , 2 ) ⊤ (7,2)^{\top} (7,2)⊤ 为根结点 (其实中位数是 6 6 6,但不存在,故选择 7 7 7)
- T l = { ( 2 , 3 ) ⊤ , ( 4 , 7 ) ⊤ , ( 5 , 4 ) ⊤ } T_l=\{(2,3)^{\top},(4,7)^{\top},(5,4)^{\top}\} Tl={(2,3)⊤,(4,7)⊤,(5,4)⊤},用于构建左子树
-
T
r
=
{
(
8
,
1
)
⊤
,
(
9
,
6
)
⊤
}
T_r=\{(8,1)^{\top},(9,6)^{\top}\}
Tr={(8,1)⊤,(9,6)⊤},用于构建右子树

-
选择第二个特征:
- 对左子树部分,排序有
- T = { ( 2 , 3 ) ⊤ , ( 5 , 4 ) ⊤ , ( 4 , 7 ) ⊤ } T=\{(2,3)^{\top},(5,4)^{\top},(4,7)^{\top}\} T={(2,3)⊤,(5,4)⊤,(4,7)⊤},中位数是 4 4 4,选择 ( 5 , 4 ) ⊤ (5,4)^{\top} (5,4)⊤ 为根结点
- T l = { ( 2 , 3 ) ⊤ } T_l=\{(2,3)^{\top}\} Tl={(2,3)⊤},用于构建左子树
- T r = { ( 4 , 7 ) ⊤ } T_r=\{(4,7)^{\top}\} Tr={(4,7)⊤},用于构建右子树
- 对右子树部分,排序有
- T = { ( 8 , 1 ) ⊤ , ( 9 , 6 ) ⊤ } T=\{(8,1)^{\top},(9,6)^{\top}\} T={(8,1)⊤,(9,6)⊤},中位数是 6 6 6,选择 ( 9 , 6 ) ⊤ (9,6)^{\top} (9,6)⊤ 为根结点 (其实中位数是 3.5 3.5 3.5,但不存在,故选择 6 6 6)
-
T
l
=
{
(
8
,
1
)
⊤
}
T_l=\{(8,1)^{\top}\}
Tl={(8,1)⊤},用于构建左子树
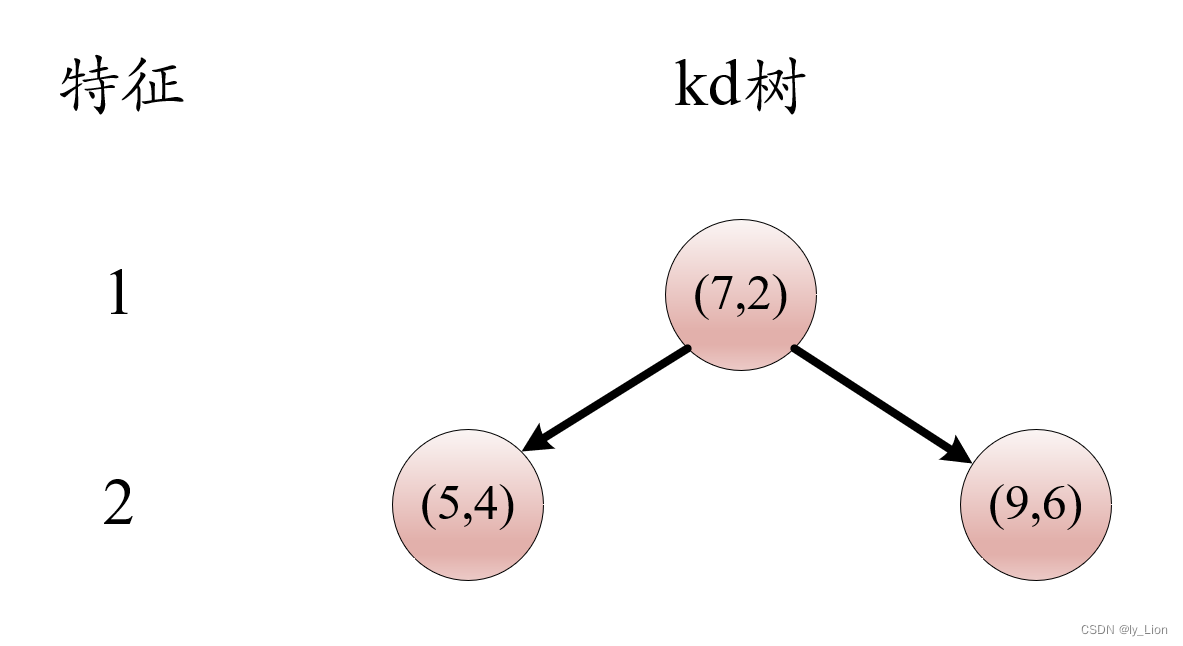
- 对左子树部分,排序有
-
选择第一个特征:
- 每个部分都是单结点了,不多赘述

- 每个部分都是单结点了,不多赘述
3.1.1.2 构造算法
注意到,其实 kd 树的构造构成就是轮流选择特征为排序依据,每一层根据选定的特征将数据进行排序,然后选择中间的数据为根结点,左边部分递归的构建左子树,右边部分递归的构建右子树。算法描述如下
- 基准情形:
- 若没有结点: 返回空树
- 若有结点:
- 根据选定的用于划分的特征,将数据集合进行排序
- 选择中间的数据点作为根结点,在该特征上小于根结点的数据用于递归生成左子树,大于根结点的数据用于递归生成右子树
- 不断推进:
- 递归生成左子树
- 递归生成右子树
注: 交替的选择特征,即假设有 m m m 个特征,根据递归的深度,按 1 , 2 , . . . , m − 1 , m , 1 , 2 , . . . , m − 1 , m , . . . 1, 2, ..., m - 1, m, 1, 2, ..., m - 1, m, ... 1,2,...,m−1,m,1,2,...,m−1,m,... 这样的顺序选择特征
3.1.1.3 kd 树划分空间
kd 树其实对应了空间的划分,对于有两个特征的数据集,他们是分散在二维平面上的点。
- 选择第一个特征进行划分: 即画一条垂直于 x x x 轴的线将点均匀的分成左右两部分
- 选择第二个特征进行划分: 即对上一步得到的两部分,分别画一条垂直于
y
y
y 轴的线,将这两部分中的点再各自均匀的分成上下两部分
… - 最后将空间划分完毕
之前举的例子的空间划分如下图所示:

3.1.2 搜索 kd 树
利用 kd 树,可以更高效的寻找最近邻,那么,先来了解一下在 kd 树中搜索某一特定数据 x 最近邻的过程。
3.1.2.1 举例: 在一棵 kd 树中搜索数据点 x 的最近邻
首先,我们有一棵已经构建好的 kd 树,树及其对应的空间划分如下图所示
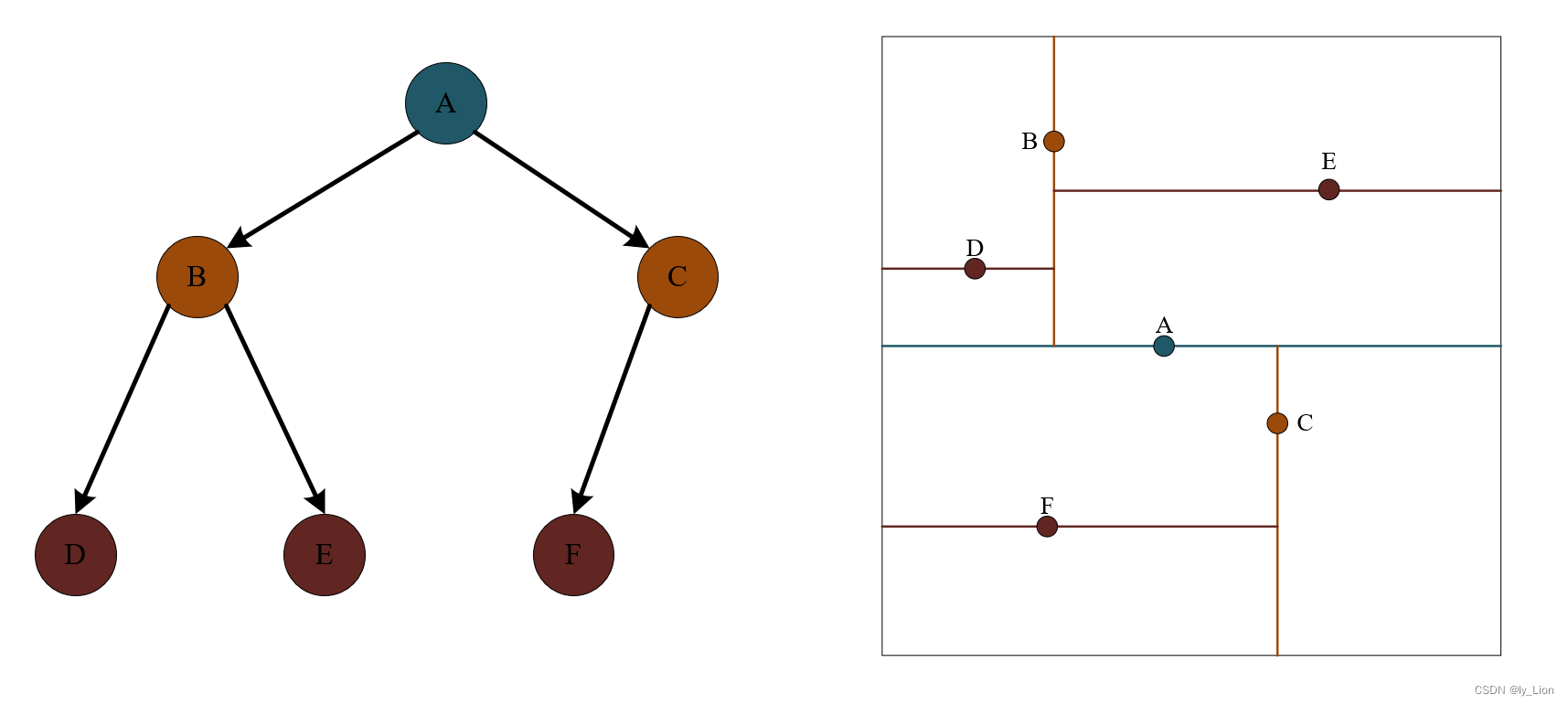
- 定位 x 在 kd 树中的位置
这显然类似于将该结点插入 kd 树的过程,只不过我们并不需要真正的插入,而只需要找到应该插入的位置。
假设点 x 的位置处于结点 D 的右儿子位置,那么我们暂时将结点 D 定为距离目标点 x 最近的点,那么比点 D 离 x 更近的点只可能存在于以点 x 为圆心,以 x 和 D 距离为半径的圆内。因为 D 是叶子结点,所以下图中斜线所覆盖区域没有更近的点了,又因为圆和 B 所在分界线有交集,故更近的点有可能存在于结点 B 的右边范围 (即对应于树中,结点 B 及其右子树中节点)

- 在 D 的兄弟节点 E 的范围内寻找,找的结果和 D 以及根结点 B 相比较,选择最近的作为当前最近点
因此,我们就找到了在下图阴影范围内的最近点是 B

- 由于圆与 A 所在分界线没有交集,因此也就不必在 B 的兄弟节点 C 中去寻找。而是直接比较 B 和 A 谁离 x 更近,那么谁就是当前最近点,由于此时阴影已经覆盖全部区域,所以得到的 B 也就是所有点中距离 x 最近的

3.1.2.2 算法: 在一棵 kd 树中搜索数据点 x 的最近邻
(1) 算法主体
- 基准情形: 若树为空,则直接返回
- 递归
- 判断递归的查找哪一棵子树,递归的查找该子树中的最近邻
- 判断是否需要再检查另一棵子树,若需要,则再递归的查找另一棵子树中的最近邻
- 最近邻和根结点中距离 x 更近则为最近邻
(2) 判断递归的查找哪一棵子树
- 比较 x 和根结点在根结点划分特征上的值大小
- 若前者更大,则递归查找右子树
- 否则递归查找左子树
(3) 判断是否需要再检查另一棵子树
- 检查以 x 为圆心,x 和当前最近邻距离为半径的圆,是否为另一子树的区域相交
- 具体地,检查 x 和当前最近邻父节点在父节点划分特征上的差值 是否大于 x 和当前最近邻 之间的距离
- 若大于,则递归的检查另一子树
- 否则,无需检查另一子树
3.1.2.3 优化: 在一棵 kd 树中搜索数据点 x 的 k k k 近邻
优化通过使用 堆 来实现。首先要知道,在 3.1.2.2 3.1.2.2 3.1.2.2 的算法中,如果我们判断不需要检查另一棵子树,那么就说明另一棵子树中的结点必然是要比检查了的子树中的点更远,所以按如下方式搜索得到 k k k 近邻。
- 递归的查找时,将查询过的点放入堆中
- 检查完第一棵子树和根结点后,若已经存放了超过 k k k 个结点,就从小根堆中取出 k k k 个最小结点即可
- 否则,检查另一棵子树,将点放入小根堆中,最后从小根堆中取出 k k k 个最小几点
3.2 实现 kd 树
3.2.1 堆
要在 kd 树中搜索 k k k 个最近邻,需要借助堆,因此先实现一个堆。
3.2.1.1 Code
import heapq
class Heap:
"""堆"""
def __init__(self, arr=None, key=lambda x: x, max_len=inf):
"""
arr: 用于构成堆的序列
key: 用于定义优先级的函数
max_len(int): 堆的最大容量, 默认不做限制
"""
self.key = key
self.max_len = max_len
if not arr:
self.h = []
else:
self.h = [(self.key(i), i) for i in arr]
heapq.heapify(self.h)
self.i = 0
def __len__(self):
return len(self.h)
def __bool__(self):
return len(self.h) != 0
def __iter__(self):
while self:
yield self.pop()
def push(self, x):
heapq.heappush(self.h, (self.key(x), self.i, x))
self.i += 1
if len(self.h) > self.max_len:
self.pop()
def top(self):
return self.h[0][-1]
def top_key(self):
return self.h[0][0]
def pop(self):
return heapq.heappop(self.h)[-1]
3.2.1.2 代码中的 API
heapq 是 python 内置的一个模块,下面介绍一下在上述代码中用到的 API
- heapq.heapify(a)
- a: 一个列表
- 作用: 将列表 a 用线性时间转化为一个 小根堆
- 注意: 是原地修改
- heapq.heappush(h, item)
- h: 一个 heapq 型的小根堆
- item: 要添加进入堆中的数据
- 作用: 将 item 压入小根堆 h
- heapq.heappop(h)
- h: 一个 heapq 型的小根堆
- 作用: 弹出堆顶元素,默认是小根堆,即返回最小值,并删除最小值
3.2.2 kd 树
下面给出的 kd 树代码直接实现了搜索 k k k 近邻功能,没有选择单独实现一个寻找最近邻的功能。
3.2.2.1 Code
class KDTree:
"""kd 树"""
class Node:
"""内部类,封装树结点"""
def __init__(self, feature, label, axis):
"""
树结点信息
Args:
feature(ndarray): 一条数据的特征向量
label(int): 该数据的标签
axis(int): 该数据在被插入到树中时, 是按第 axis 个特征来排序
"""
self.feature = feature
self.label = label
self.axis = axis
self.left = None
self.right = None
def __init__(self, X, Y):
"""
构造方法: 构造一棵 kd 树
Args:
X(ndarray): 训练数据的特征矩阵
Y(ndarray): 训练数据的标签向量
"""
self.root = self.build(X, Y)
def build(self, X, Y, split_axis=0):
"""
基于训练数据建立 kd 树
Args:
X(ndarray): 训练数据的特征矩阵
Y(ndarray): 训练数据的标签向量
split_axis(int): 在递归的当前层, 以第 split_axis 个特征作为排序依据
Returns:
建立好的 kd 树根结点
"""
# 1. 基准情形: 数据集为空, 返回空树
if not len(X):
return None
# 2. 递归的生成 kd 树
# 2.1 在递归的当前层进行的操作
# 2.1.1 根据选定的作为排序依据的特征, 求出排序后位于中间的数据点下标
median_idx = np.argpartition(X[:, split_axis], len(X) // 2, axis=0)[len(X) // 2]
# 2.1.2 取出该点作为树根, 并划分出作为其左子树和右子树的数据点集合
# 处理该结点
split_point = float(X[median_idx, split_axis]) # 相当于 float(X[median_idx][split_axis]
feature = X[X[:, split_axis] == split_point] # 取出该数据点的特征向量
label = Y[X[:, split_axis] == split_point] # 取出该数据点的标签
node = self.Node(feature, label, split_axis) # 构造结点
# 取出左子树和右子树的点集合
lsubtree_feature = X[X[:, split_axis] < split_point] # 取出用于构建左子树的数据点的特征向量集合与标签集合
lsubtree_label = Y[X[:, split_axis] < split_point]
rsubtree_feature = X[X[:, split_axis] > split_point] # 取出用于构建右子树的数据点的特征向量集合与标签集合
rsubtree_feature = Y[X[:, split_axis] > split_point]
# 3. 递归的生成左子树和右子树
node.left = self.build(lsubtree_feature, lsubtree_label, 1 - split_axis)
node.right = self.build(rsubtree_feature, rsubtree_feature, 1 - split_axis)
# 4. 返回生成的 kd 树
return node
def query(self, x, k):
"""
在当前 kd 树中,寻找 x 的 k 个最近邻
Args:
x(ndarray): 一条测试数据的特征向量
k(int): 寻找最近邻的个数
Returns:
k 个最近邻
"""
return self._query(self.root, x, k)
def _query(self, root, x, k):
"""
辅助方法: 寻找 x 的 k 个最近邻
Args:
root: 要搜索 kd 树的树根
x(ndarray): 一条测试数据的特征向量
k(int): 寻找最近邻的个数
Returns:
k 个最近邻
"""
# 1. kd 树为空
if not root:
return Heap(max_len=k, key=lambda xy: np.linalg.norm(x - xy[0], axis=-1)) # xy, 即 [feature, label] 中的 feature
# 2. 查找数据点 x, 应该被插入在 kd 树中的哪个叶结点下, 以此叶结点为当前最近点
# 具体的, 若其按根的划分特征比较, 应该在根的左侧, 就递归的在左子树中查找, 否则递归的在右子树中查找
if x[root.axis] <= root.feature[0][root.axis]:
ans = self._query(root.left, x, k)
sibling = root.right # 当在左子树中找不够 k 个最近邻时, 就要到它的兄弟 (根的右儿子) 中递归的找
else:
ans = self._query(root.right, x, k)
sibling = root.left
# 3. 将根结点的特征向量和标签打包成一对元组, 存入堆中
# 即, 递归的查找完某一子树后, 堆中存放了根及其该子树中的点
for curr_x, curr_y in zip(root.feature, root.label):
ans.push((curr_x, curr_y))
# 4. 若查找到的邻居数少于 k 个, 或以 x 为圆心, 以 x 和当前最近点为半径的圆和另一子树区域相交, 则递归的查找另一子树
if len(ans) < k or -ans.top_key() > abs(x[root.axis] - root.feature[0][root.axis]):
other_ans = self._query(sibling, x, k)
while other_ans:
other_x, other_y = other_ans.pop()
ans.push((other_x, other_y))
# 5. 返回堆, 其中包含了 ≥ k 个最近邻, k 次 deleMin 即可取出 k 个最近邻
return ans
3.2.2.2 代码中的 API
- 内部类
- 通常仅含有一个 __init__() 方法, 用于封装结点信息
- float(a)
- a: 字符串或者整数
- 作用: 内置函数,用于将字符串和整数转换成浮点数
- numpy 中的 ndarray 特性
- A [ i , j ] A[i, j] A[i,j] 相当于 A [ i ] [ j ] A[i][j] A[i][j]
- zip(a, b, c, …)
- a, b, c, …: 均为可迭代对象
- 作用: 每个可迭代对象的相同下标元素被打包成一个元组
- 注意:
- 可迭代对象可以是元组,列表之类,各个可迭代对象不必为同一类型
- 各个可迭代类型长度不必相同,最终返回的长度为最短的对象长度
- python3 版本中,zip 返回的是一个对象,要显示内容,需要使用 list(r),其中 r 是 zip 返回的对象
4. 实现 kd 树优化的 k k k-NN
kd 树优化的 k k k-NN 和原始版本的实现,差别主要在两个部分,即 fit,_knn 和 _predict。具体地,fit 中接收训练数据时,就是用训练数据构建一棵 kd 树,_predict 预测获取 k k k 个最近邻的下标时直接使用 kd 树的 query 方法即可,因此原始版本中的 _knn 辅助方法也就可以删除掉。
def fit(self, X, Y):
"""
训练方法: k-NN 没有显式的训练过程, 所以这里只是接收训练数据
Args:
X(ndarray): 训练数据的特征矩阵
Y(ndarray): 训练数据的真实类别向量
"""
self.tree = KDTree(X, Y) # 变动 1: self.tree = KDTree(X, Y)
self.k = min(self.k, len(X))
def _predict(self, x):
"""
辅助方法: 使用当前模型,预测某一数据 x 的类别 y
Args:
x(ndarray): 一条数据的属性向量
Returns:
预测结果,即类别 y
"""
# 1. 确定 k 近邻, 获取它们的下标
topk_idx = self.tree.query(x, self.k) # 变动 2: topk_idx = self.tree.query(x, self.k)
# 2. 根据下标获取它们的类别
topk_y = self.Y[topk_idx]
# 3. 选择数量最多的类别返回
return np.argmax(np.bincount(topk_y))








 本文深入探讨了k近邻(k-NN)算法,包括模型概述、k值选择、距离度量和分类决策规则。详细解释了k-NN的算法流程,并给出了Python实现。同时,介绍了kd树这一数据结构,阐述了kd树的构造和搜索过程,以及如何利用kd树优化k-NN算法,提高搜索效率。最后展示了kd树优化的k-NN代码实现。
本文深入探讨了k近邻(k-NN)算法,包括模型概述、k值选择、距离度量和分类决策规则。详细解释了k-NN的算法流程,并给出了Python实现。同时,介绍了kd树这一数据结构,阐述了kd树的构造和搜索过程,以及如何利用kd树优化k-NN算法,提高搜索效率。最后展示了kd树优化的k-NN代码实现。
















 994
994

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








