CSI RS Codebook 5GNR码本

什么是码本？

码本在不同场景下可能有不同的含义，但在CSI-RS（信道状态信息参考信号）的上下文中，码本是一组预编码器（即一组预编码矩阵）。

换句话说，码本是一种矩阵（具有复数值元素的矩阵），用于将数据比特（如PDSCH的比特）转换为另一组映射到每个天线端口的数据。

两种类型的码本：类型I和类型II

在5G中定义了两种类型的码本：

• 类型I：基于与LTE码本相同的逻辑。NR类型I码本略微复杂一些，并且支持更多种类的矩阵。基本上，这种类型使用的是一组预定义的矩阵，由UE（用户设备）报告和RRC（无线资源控制）配置选择。
  参考文献：[33]

• NR类型II：并不是基于预定义的表格，而是基于一个具有大量参数的特定数学公式设计的。这些公式中的参数由RRC和UE报告决定。如果查看类型II码本，您不会看到像类型I码本中那样多的不同表格，但会注意到定义预编码矩阵的公式更加复杂。使用这些复杂的公式和大量参数，类型II能够应用比类型I更复杂的预编码矩阵。
  参考文献：[33]

• 类型II：基于更详细的CSI报告，主要为MU-MIMO（多用户MIMO）设计。

• 类型I和类型II的结构：这两种类型均由2维DFT（离散傅里叶变换）基于波束的网格构成，并使CSI反馈的波束选择以及PSK（相位键控）基于两种极化之间的联合工作。
  参考文献：[34]

• 类型I与类型II的区别：类型I报告仅定义了选定波束的相位，而非幅度；而类型II码本基于CSI反馈报告了所选波束的宽带和子带的幅度信息。
  参考文献：[34]

• 类型I和类型II的主要区别：类型I从一组波束中选择一个特定的波束，而类型II选择一组波束并线性组合组中所有的波束。详细解释可参考文献：[38]

接收方是否需要知道预编码矩阵才能解码接收信号？

接收方是否需要知道预编码矩阵才能解码接收的信号？答案取决于数据传输方案的设计方式。大致来说，存在以下两种实现方式：

1. 在情况1中，接收方不需要知道预编码矩阵的信息。
2. 在情况2中，接收方需要了解预编码矩阵的信息。

详细信息请参见文献第11章（参考文献 [10]）。

< Case 1 >

信道估计器（Channel Estimator）可以通过已知的参考数据推导出预编码器 $W$ 和无线信道 $H$ 的总体影响，理论上无需了解 $W$ 的具体信息。一旦该总体影响被估计出来，接收方便可以利用从参考数据中估计出的信息，对用户数据进行均衡和解码。

< Case 2 >

从哪里开始？——理解基础术语

当我开始阅读38.214-5.2.2.2章节时，我遇到的第一个问题是要弄清楚一些奇怪的单字符参数的含义，比如$N_1$、$N_2$、$O_1$、$O_2$，这些术语在TS（技术规范）中并没有明确定义，还有一些其他的术语，如“Panel”（即单面板、多面板，如RRC消息中所示）。当某些术语没有在TS文档中清晰定义时，很可能它们是在某些TDocs（R1-XXXXX）中描述的，并转移到TS文档中但没有清楚解释。因此，我开始搜索TDocs关于这个主题的文档，并找到了一些TDoc参考文献[1]、[5]、[6]、[7]、[8]，这些文献似乎是这个主题的起源，还有其他文献如参考[2]和参考[3]，帮助我们理解其他像“Panel”这样的术语。

注意：基本上，NR CSI码本设计的大部分基本概念都是继承自LTE Rel 13 FD-MIMO码本设计的。你会在LTE TDocs中找到许多详细描述和图表。请查看参考[14]、[3]、[15]中的链接，并查看CSI码本的相关文档。

$N_1$、$N_2$、$O_1$、$O_2$：这些单字符参数的定义在R1-1612661中说明，如下所示。$N_1$、$N_2$由水平和垂直方向上的天线数量决定。$O_1$、$O_2$ 表示DFT过采样。

注意：
O1 和 O2 的整体功能是在波束管理（波束跟踪）过程中确定波束的扫描步长。O1 确定水平方向的扫描步长，而 O2 确定垂直方向的扫描步长。简而言之，O1 和 O2 的值越大，波束的扫描步长越小（即角度越精细）。

我找到了三星白皮书中更清晰的图示（如下所示），它可以将波束矩阵与垂直和水平方向的波束角度相关联。

将TDocs与TS连接

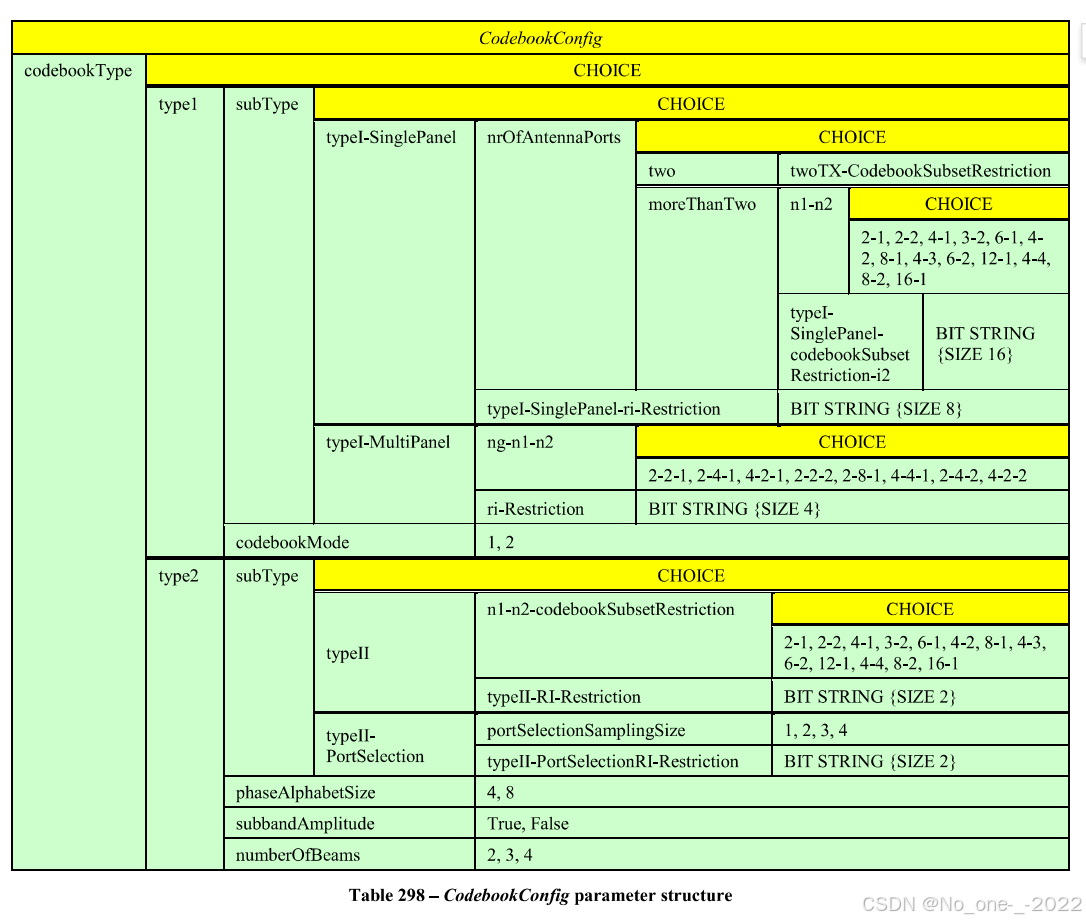
如上所述，仅通过阅读3GPP TS规范，很难理解关于CSI-RS码本的说明。因此，在我的情况下，我经常参考各种TDocs，有时还会查阅关于5G物理层的教材。然而，很多情况下，很难找到TDoc/教材所描述的内容与3GPP TS规范之间的直接联系。在本节中，我将提供一些提示和技巧，帮助你将通常在TDoc/教材中看到的内容与3GPP TS规范进行关联。

我首先要向你展示的是下面的链接。在大多数TDocs和教材中，他们将CSI码本描述为 $W=W_1\ast W_2$（两个矩阵的组合），但3GPP TS并未以相同的方式明确描述。3GPP TS只列出了一大堆表格。TDoc中的码本与3GPP TS之间的连接可以通过以下方式进行说明。

注意事项：
有了这种通用结构后，选择一个你认为可以处理的简单PMI表，并像我在W矩阵推导示例中那样用笔推导该矩阵。这个推导中可能存在一些错误，但至少它帮助我更清晰地理解了矩阵的结构和含义。

注意：通过这份笔记，我希望你能够对如何针对特定的CSI参考设置推导预编码矩阵有一个非常具体的理解。一旦你成功推导出这样的矩阵，那么你就需要了解如何解释矩阵（即，矩阵如何应用于要传输的数据）。为了直观地理解这些矩阵，我建议练习如何使用复杂矩阵来变换一组复数数据（I/Q数据）。为此类练习，我发布了另一种风格的笔记在矩阵复数。

W1 和 W2 的推导

如上所述，W矩阵最初是设计为两个矩阵W1和W2的乘积（关于原始设计，参见[参考文献1]和[参考文献13]）。但对我来说，理解该设计的实际概念很困难，尤其是当我大约一年前第一次阅读时，不知道每个矩阵到底代表什么。后来我在一个博客中找到了些许线索（参见[参考文献11]），但并不全面，几乎忘记了这个概念，直到笔记读者Daniel (HyungJong) Noh提起了这个问题。Daniel比我更快地理解了如何推导出W1和W2，并分享了一个示例，展示了这两个矩阵的推导过程，并允许我与读者分享。

在进入HyungJong分享的示例之前，我想给你一些额外的笔记，以帮助你（以及我自己）理清思路。

首先，我假设现在大家都知道 $W$ 定义如下：

$$W=W_1\ast W_2$$

基于参考文献[1]、[11]、[13]以及34.214，我们可以进一步扩展这个等式。我认为 $W_1$ 的含义现在对你来说应该很清楚了，但从这个定义中 $W_2$ 的含义可能依然难以理解。你将在HyungJong的示例中看到更具体的 $W_2$ 形式。（注意：⊗表示Kronecker积）。

现在让我们按照HyungJong的示例进行分析。在此示例中，我们假设以下情况（与W矩阵计算中的示例01相同），但 $i_{1,1}$、$i_{1,2}$、$i_2$未指定，即它们保持为通用变量）。

• CSI端口数量 = 4
• N1 = 2, N2 = 1, O1 = 4, O2 = 1

让我们从计算 $\mathbf{B}$ 开始。根据 Linking TDoc to TS 部分中的定义， $\mathbf{B}$ 可以如下计算。

基于此，我们可以构造出 $W_1$ 为

根据此示例给出的条件，您可以如下定义 $W_2$ 矩阵。您可以参考[参考文献11]和参考文献[32]的第6.12.4.2.1节，了解有关 $W_2$ 定义的更多详细信息。

有了 $W_1$ 和 $W_2$，我们可以计算出 $W$ 的结果为

如果你根据本节开头所示的定义，以稍微不同的方式修改这个 $W$ 矩阵，你可以将这个结果改写如下，你可能会意识到它与38.214表格中描述的形式相同，并且能够理解该表格中的公式是如何设计的。

W矩阵推导示例

在本节中，你推导出的最终矩阵将包含复数元素。用户数据（例如PDSCH数据）同样以复数的形式（I和Q数据）呈现。最终你应该能够在脑中可视化这些矩阵的特性，以便理解它们的意义。这里有另一种类型的笔记，可以帮助你直观地理解包含复数元素的矩阵如何应用于复杂数据。可以参考矩阵复数。

示例01 > p4，1 Layer，$N_1=2$，$N_2=1$，$O_1=4$，$O_2=1$，$i_{1,1}=0$，$i_{1,2}=0$，$i_2=0$

我们假设PMI表按照以下表格配置（表5.2.2.2.1-5）。

假设我们有以下报告和天线配置：

• CSI端口数量 = 4
• $N_1=2$，$N_2=1$，$O_1=4$，$O_2=1$
• $i_{1,1}=0$，$i_{1,2}=0$，$i_2=0$
• 这表示：$l=i_{1,1}=0$，$m=i_{1,2}=0$，$n=i_2=0$

现在，将这些参数代入所有方程以推导最终矩阵。如果你发现任何错误，请告诉我。首先，我们计算 $u_m$ 向量
$$u_m=\{\begin{array}{ll}\left[1e^{j\frac{2\pi m}{0_2{N}_2}}\dots e^{j\frac{2\pi m(N_2-1)}{0_2{N}_2}}\right]& ,N_2>1\\ 1& ,N_2=1\end{array}$$

在这个例子中，$N_2$ 为 1。因此，$u_m$ 如下所示：
$$u_m=1$$同理，$v_l$ 可以表示为$$v_l={\left[\begin{array}{cccc}1& \frac{j2\pi l}{N_1{O}_1}& ...& e^{\frac{j2\pi (N_1-1)l}{N_1{O}_1}}\end{array}\right]}^T$$接下来，计算 $v_{l,m}$ 向量。
$$v_{l,m}=v_l\otimes u_m={\left[u_m{e}^{j\frac{2\pi l}{O_1{N}_1}}{u}_m\dots e^{j\frac{2\pi l(N_1-1)}{O_1{N}_1}}{u}_m\right]}^T$$在这个例子中，$l=0$，$m=0$，所以 $v_{l,m}$ 变为如下形式：
$$v_{0,0}={\left[1e^{j\frac{2\pi 0}{4}}=1\right]}^T$$

将向量转置后，我们得到如下向量：

$$v_{0,0}=\left[\begin{array}{c}1\\ e^{j\frac{2\pi 0}{4}}=1\end{array}\right]=\left[\begin{array}{c}1\\ 1\end{array}\right]$$

现在使用参数 $n$ 计算 ${\phi }_n$ 值。
$${\phi }_n=e^{j\pi n/2}$$将例子中的 $n$ 值代入，得到如下结果：
$${\phi }_0=e^{j\pi 0/2}=1$$将上面获得的所有向量代入矩阵$$W_{l,m,n}^{(1)}=\frac{1}{\sqrt{P_{CSI-RS}}}\left[\begin{array}{c}{v}_{l,m}\\ {\phi }_n{v}_{l,m}\end{array}\right]$$

代入示例中的 $l,m,n$ 值，我们得到以下向量：
$$W_{0,0,0}^{(1)}=\frac{1}{\sqrt{P_{CSI-RS}}}\left[\begin{array}{c}{v}_{0,0}\\ {\phi }_0{v}_{0,0}\end{array}\right]$$经过完整的计算，得到最终的矩阵（向量）为：

$$W_{0,0,0}^{(1)}=\frac{1}{\sqrt{P_{CSI-RS}}}\left[\begin{array}{c}1\\ 1\\ 1\left[\begin{array}{c}1\\ 1\end{array}\right]\end{array}\right]=\frac{1}{\sqrt{P_{CSI-RS}}}\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]$$

$W$ 右上角的上标 $(1)$ 与传输层（Layer）对应

注意：现在最后一步是理解这个向量的含义。最好的方法是你自己创建一组 IQ 数据，并将这个向量与 IQ 数据相乘，看看原始 IQ 数据如何变化。如果你不想自己做这个，那么第二好的方法是查看我的可视化数学笔记。可以参考 这个页面。另外，你也可以将这个矩阵解释为一个波束，如 这个页面 所示。

示例03 > p4，2 Layer，$N_1=2$，$N_2=1$，$O_1=4$，$O_2=1$，$i_{1,1}=0$，$i_{1,2}=0$，$i_{1,3}=0$，$i_2=0$

• CSI端口数量 = 4
• $N_1=2$，$N_2=1$，$O_1=4$，$O_2=1$
• $i_{1,1}=0$，$i_{1,2}=0$，$i_{1,3}=0$，$i_2=0$
• 这表示：$l=i_{1,1}=0$，$l^{\prime }=i_{1,1}+k_1=0$，$m=i_{1,2}=0$，$m^{\prime }=i_{1,2}+k_2=0$，$n=i_2=0$

首先我们推导向量 $u_m$

$$u_m=\{\begin{array}{ll}\left[1e^{j\frac{2\pi m}{o_2{N}_2}}\cdots e^{j\frac{2\pi m(N_2-1)}{o_2{N}_2}}\right]& ,N_2>1\\ 1& ,N_2=1\end{array}$$

由于在本例中给定条件 $N_2=1$，因此 (u_m) 变为 1：$$u_m=1$$接下来我们推导向量 $v_{l,m}$

$$v_{l,m}={\left[u_m{e}^{j\frac{2\pi l}{O_1{N}_1}}{u}_m\cdots e^{j\frac{2\pi l(N_1-1)}{O_1{N}_1}}{u}_m\right]}^T$$

因为在本例中 $l$ 和 $m$ 都是 0，所以向量变为如下形式：

$$v_{0,0}={\left[1e^{j\frac{2\pi \cdot 0}{42}}=1\right]}^T$$

对向量进行转置并简化，我们得到
$$v_{0,0}=\left[\begin{array}{c}1\\ e^{j\frac{2\pi 01}{42}}1\end{array}\right]=\left[\begin{array}{c}1\\ 1\end{array}\right]$$计算给定 $n$ 值时的 ${\phi }_0$

我们得到如下的 ${\phi }_0$ 值：$${\phi }_0=e^{j\pi 0/2}=1$$使用与 $v_{l,m}$ 相同的方法，我们可以计算向量 $v_{l^{\prime },m^{\prime }}$
$$v_{l^{\prime },m^{\prime }}={\left[1e^{j\frac{2\pi l^{\prime }}{O_1{N}_1}}{u}_{m^{\prime }}\cdots e^{j\frac{2\pi l^{\prime }(N_1-1)}{O_1{N}_1}}{u}_{m^{\prime }}\right]}^T$$代入 $l^{\prime }$ 和 $m^{\prime }$ 的值，我们得到：
$$v_{0,0}=\left[\begin{array}{c}1\\ e^{j\frac{2\pi 01}{42}}1\end{array}\right]=\left[\begin{array}{c}1\\ 1\end{array}\right]$$现在将我们推导出的所有向量和数值代入最终的矩阵
$$W_{l,l^{\prime },m,m^{\prime },n}^{(2)}=\frac{1}{\sqrt{P_{CSI-RS}}}\left[\begin{array}{cc}{v}_{l,m}& v_{l^{\prime },m^{\prime }}\\ {\phi }_n{v}_{l,m}& -{\phi }_n{v}_{l^{\prime },m^{\prime }}\end{array}\right]$$通过将参数 $(l,l^{\prime },m,m^{\prime },n)$ 代入矩阵，可以得到如下形式：
$$W_{l,l^{\prime },m,m^{\prime },n}^{(2)}=\frac{1}{\sqrt{P_{CSI-RS}}}\left[\begin{array}{cc}{v}_{0,0}& v_{0,0}\\ {\phi }_0{v}_{0,0}& -{\phi }_0{v}_{0,0}\end{array}\right]$$然后，将我们之前推导出的向量和数值代入矩阵中，最终得到结果如下：
$$W_{0,0,0,0,0}^{(2)}=\frac{1}{\sqrt{P_{CSI-RS}}}\left[\begin{array}{cc}\left[\begin{array}{l}1\\ 1\end{array}\right]& \left[\begin{array}{l}1\\ 1\end{array}\right]\\ 1\left[\begin{array}{l}1\\ 1\end{array}\right]& -1\left[\begin{array}{l}1\\ 1\end{array}\right]\end{array}\right]=\frac{1}{\sqrt{P_{CSI-RS}}}\left[\begin{array}{rr}1& 1\\ 1& 1\\ 1& -1\\ 1& -1\end{array}\right]$$