TASK02|GitModel线性代数

线性方程组与向量

采用的摄像头对动物计数时候，只能统计有多少个头，有多少只脚.现在摄像头采集到的数据是一共有10个头，28只脚，请问鸡兔各有几只？
$x+y=10$
$2x+4y=28$

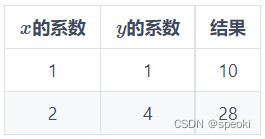
系数矩阵

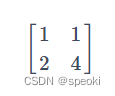
结果矩阵

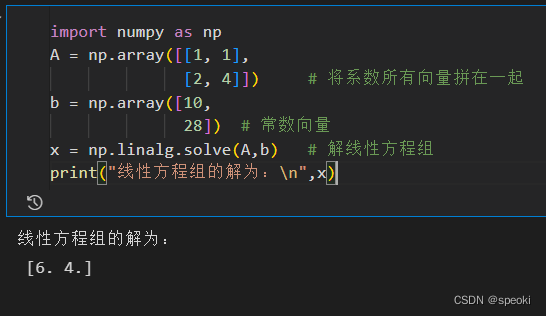
A = np.array([1,1],[2,4])#定义系数矩阵
b = np.array([10,28])#定义结果矩阵
x = np.linalg.solve(A,b);np.linalg以一个矩阵的方式求解线性矩阵方程

求出来x,y的值所组成的矩阵

向量空间、矩阵、行列式以及范数

Ginger希望多养几种动物，近日他又引入了几只公鸡和几只鸭子，现在采集到的数据是一共有14个头，40只脚，请问鸡兔鸭各有几只？
在这里有三个变量，我们无法根据A和b求得线性方程的唯一解

假设鸭子的数目是$z$只
$x+y+z=142x+4y+2z=40$

A=np.array([1,1,1],[2,4,2])
b=np.array([14,40])
x=np.linalg.solve(A,b)

我们需要引入动物眼睛的变量才能确定解

$x+y+z=14$
$2x+4y+2z=40$
$2x+2y+2z=28$

A=np.array([1,1,1],[2,4,2],[2,2,2])
b=np.array([14,40,28])
x=np.linalg.solve(A,b)

还是无法得出结果的，因为这个矩阵是一个奇异矩阵。行列式的值为零，新增式子对与求解方程没有作用

向量的运算法则

1.数乘
2.向量的加法

import numpy as np
x=np.array([1,2,3])
x=np.array([4,5,6])
print("x={},y={}".format(x,y))
print("x的维度为{}".format(x.shape))
print("x+y={}".format(x+y))
k=3
print("kx = {}".format(k*x))
print("3x+2y={}".format(3*x+2*y))

向量的线性相关与线性无关

判断方程有唯一解的方法

1.系数矩阵的秩和增广矩阵的秩大小等于未知数的个数

2.(1)未知数个数等于方程的个数
(2)系数行列式 $|A|\ne 0$则这个方程组是有唯一解的.

计算方阵的行列式

A=np.array([3,4,5],[3,3,3],[4,4,4])
np.linalg.det(A)
print(np.linalg.det(A))
B=np.array([2,2,2,2],[2,1,0,0],[0,3,1,0],[2,0,0,4])
B_det = np.linalg.det(B)
print(np.linalg.det(B_det))

使用克拉默法则

D=np.array([[2.,1,-5,1],[1,-3,0,-6],[0,2,-1,2],[1,4,-7,6]])
D_det = np.linalg,det(D)
D1 = np.array([[8.,1,-5,1],[9,-3,0,-6],[-5,2,-1,2],[0,4,-7,6]])
D1_det = np.linalg.det(D1)
x1=D1_det/D_det
print("\n x1={:.2f}".format(x1))

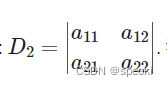
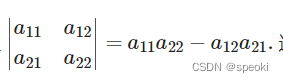
对应的向量的关系

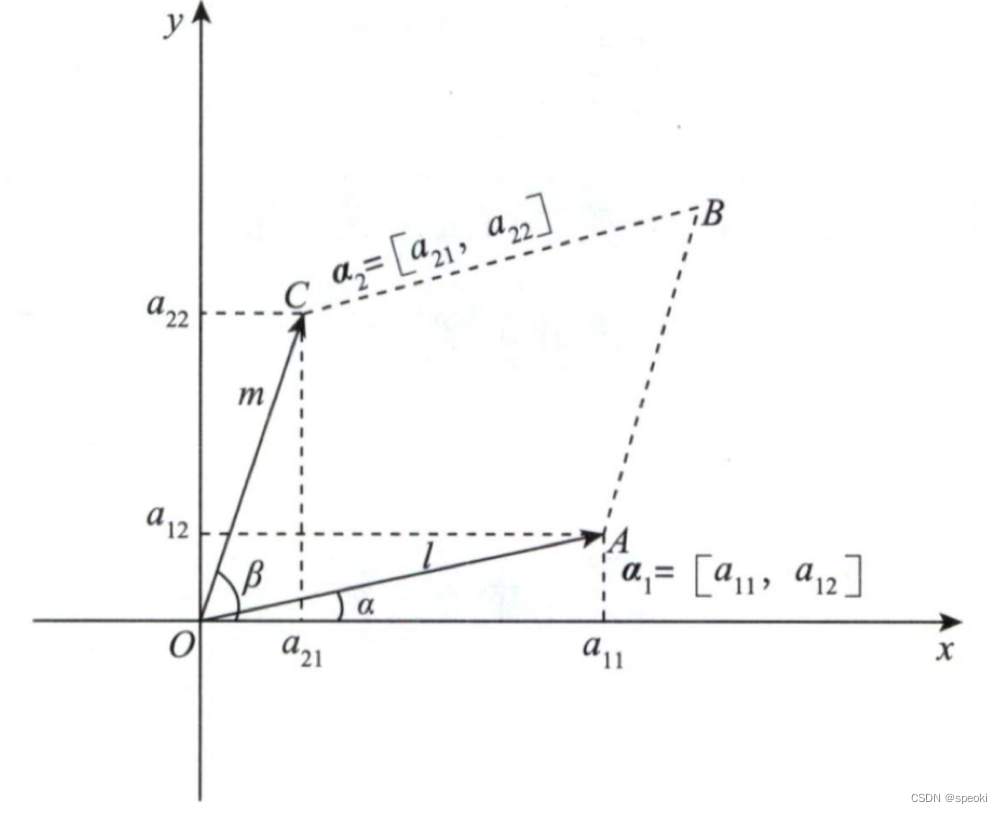
向量的几何意义

$\begin{array}{rl}{S}_{\square OABC}& =l\cdot m\cdot \sin (\beta -\alpha )\\ & =l\cdot m(\sin \beta \cos \alpha -\cos \beta \sin \alpha )\\ & =l\cos \alpha \cdot m\sin \beta -l\sin \alpha \cdot m\cos \beta \\ & =a_{11}{a}_{22}-a_{12}{a}_{21}\end{array}$

$\left|\begin{array}{ll}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|=a_{11}{a}_{22}-a_{12}{a}_{21}=S_{\square OABC}$

矩阵

两个矩阵相乘

A=np.array([[1,2],[1,-1]])
B=np.array([[1,2,3],[-1,1,2]])
C = np.array([[1, 2],[3, 4]])
print("{}".format(A.shape))
print("{}".format(B.shape))
print("{}".format(np.matmul(A,B)))#AB
print("A+C = \n", A + C) # A+C 
print("3*A = \n", 3 * A) # 3*A

1.单位矩阵

np.eye(3)

2.初等矩阵

交换矩阵的两行

P = np.array([[0, 1],[1, 0]])
np.matmul(P, A) # 交换了矩阵的两行
P = np.array([[2, 0],[0, 1]])
np.matmul(P, A) # 第1行乘2

矩阵的一行加到另外一行
注意左乘和右乘的区别
行变换左乘，列变换右乘

P=np.array([[1,0],[1,1]])
np.matmul(P,A)

矩阵求逆
矩阵可逆必为方阵

import numpy as np
A=np.array([[1,2],[3,4]])
print(np.linalg.det(A))#检测是否为奇异矩阵
print(np.linalg.inv(A))
A_inv=np.linalg.inv(A)
print(np.matmul(A,A_inv))#验证

伪逆的定义
$A{A}^{g}A=A$,则称
$A^g$为$A$的伪逆(广义逆).

相似矩阵的定义
$A=P^{-1}BP$
A与B相似

对角矩阵的定义

A = np.array([[1, 0, 0],
              [0, 2, 0], 
              [0, 0, 3]])

找出一个A的相似且为对角矩阵
使得此矩阵特征值${\lambda }_i$满足

$Ax={\lambda }_{i}x$

A=np.array([-2,1,1],[0,2,0],[-4,1,3])
lamb,p=np.linalg.eig(A)#求解特征值和特征向量
求出来的特征向量对角化
np.matmul(np.linalg.inv(p),np.matmul(A,p))

经过数值过滤

# 数值过滤
res = np.matmul(np.linalg.inv(p),np.matmul(A,p))
res[np.abs(res) <1e-6] = 0 
print(res)

$\Lambda =\left[\begin{array}{lllc}-1& & & \\ & 2& & \\ & & 2& \end{array}\right]$

正交矩阵

$A^{T}A=A{A}^T=I$
$A^{-1}=A^T$
性质：A的各行是单位向量且两两正交（垂直），又或者说A的各列是单位向量且两两正交（垂直）
${\alpha }_i\cdot {\alpha }_j^T=0(i\ne j)$
${\alpha }_i\cdot {\alpha }_i^T=1$

行列式的绝对值描述了向量围成的面积/体积，因此正交矩阵的行列式要么是1，要么是-1。
$\begin{array}{rl}& 1=\det (I)=\det \left(A^{T}A\right)=\det \left(A^T\right)\det (A)=\det (A{)}^2\\ & \Rightarrow \det (A)=\pm 1\end{array}$

施密特正交化

from scipy.linalg import *
A = np.array([[1,2,3],[2,1,3],[3,2,1]])
B=orth(A)#正交化，奇异值分解不是施密特正交化
np.matmul(B,np.transpose(B))#单位矩阵
res = np.matmul(B,np.transpose(B))#数值过滤
res[np.abs(res) <1e-6] = 0