几个常见的非初等函数

  在多个激励共同作用下，其响应恒等于每个激励单独引起的响应之和。这种现象称为线性现象。线性性质使得对这类现象的数学描述大为简化，它是线性系统理论的基础。

本篇博客将简单介绍以下几个常用的非初等函数。

rect 矩形函数(Rectangular Function)

sinc 函数(Sinc Function)

三角形函数(Triangle Function)

符号函数(Signum Function)

阶跃函数(Step Function)

圆柱函数(Circle Function)

斜坡函数(Ramp Function)

高斯函数(Gauss Function)

1、rect函数（Rectangular Function）

1.1 rect函数（One-Dimension）

 

表示为以为中心，a为宽度（a>0），高度为1的矩形。

（1）当x为时间变量时，可表示一个时间方波（电路中的开关作用；相机快门作用）

（2）当x为空间变量时，可表示一个狭缝、矩孔的透过率

         它与某函数相乘时，可限制函数自变量的范围，起到截取的作用，故又常称之为“门函数”。

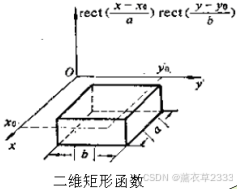
1.2 rect函数（2D Rectangular Function）

        可用来描写不透明屏上的矩形孔的透过系数。

 

2、sinc函数（ Sinc Function）

零点位于x-  = na（n = 1,2,...）

sinc函数常用来描述狭缝或者矩孔的夫琅和费衍射

3、三角形函数（Triangle Function）

 

图形是以为中心，底边长为2a，高度为1，面积为a的等腰三角形。

三角形函数可用来表示光瞳为矩形的非相干成像系统的光学传递函数。

4、符号函数（Signum Function)）

 

        sgn函数可用于在某一点逆转一个函数的极性，其宽度和面积的概念是无意义的，常数a的大小无意义，其正负仅仅决定函数的取向或极性，一般取1。

        可利用符号函数来描述某孔径的一半嵌有相位板的复振幅透过率。

5、阶跃函数（Step Function）

        step函数的宽度和面积的概念是无意义的，常数a的大小无意义，其正负仅仅使函数在某一 点打开或关闭，一般取1。

        常用它表示直边 (或刀口 )的透过率。

5.1 阶跃信号的单边特性

        阶跃信号具有非常明显的单边特性，它和其他信号相乘可以截断信号。实际中常利用它的这个特性表示单边信号或区间信号，即信号的加窗或取单边。

6、圆柱函数（Circle Function）

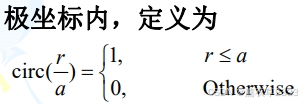
圆柱函数常用来表示圆孔的透过率。

7、斜坡函数（Ramp Function）

7、高斯函数（Gauss Function）

         高斯函数的傅立叶变换是另一个高斯函数，高斯函数属于初等函数，但它没有初等不定积分，其不定积分是误差函数。

        高斯函数常用来描述激光器发出的高斯光束。