Transformer模型详解——语音信号处理学习（一）

已于 2024-07-10 11:56:03 修改
阅读量2.6k 收藏 32
点赞数 7
分类专栏： 声音信号处理学习 文章标签： transformer 信号处理 学习 人工智能
于 2023-10-21 12:37:14 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/m0_56942491/article/details/133959712
版权

参考文献：

[1] Transformer模型详解（图解最完整版） - 知乎 (zhihu.com)

[2] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[J]. Advances in neural information processing systems, 2017, 30.

[3] Transformer - YouTube

[4] Transformer模型（总结） - 知乎 (zhihu.com)

目录

一、Transformer 整体结构

二、Transformer 的输入

2.1 单词 Embedding

2.2 位置 Embedding

三、Self-Attention（自注意力机制）

3.1 Self-Attention 结构

3.2 Q, K, V 的计算

3.3 Self-Attention 的输出

3.4 Multi-Head Attention

四、Encoder 结构

4.1 Add & Norm 结构

4.2 Feed Forward

4.3 组成 Encoder

五、Decoder 结构

5.1 第一个 Multi-Head Attention

5.2 第二个 Multi-Head Attention

5.3 Softmax 预测输出单词

一、Transformer 整体结构

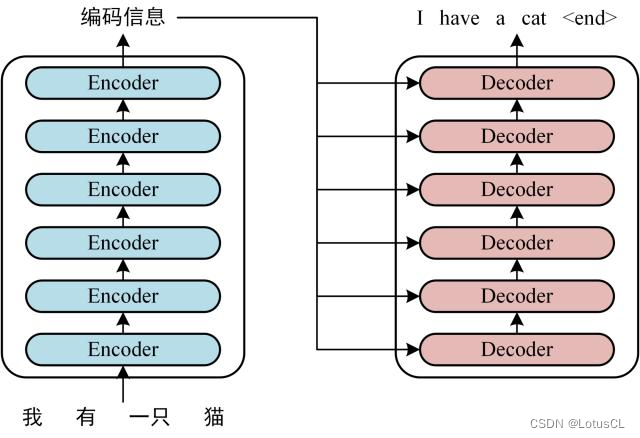
  • Transformer 由 Encoder 和 Decoder 两个部分组成，Encoder 和 Decoder 都包含 6 个 block。

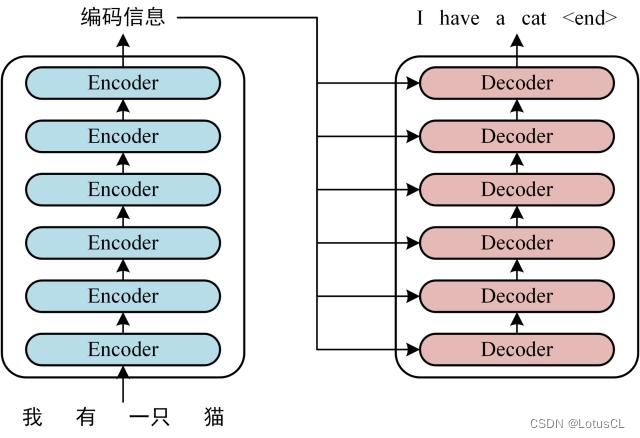
  • Transformer由一个编码器（Encoder）堆栈和一个解码器（Decoder）堆栈组成，每个编码器堆栈（解码器堆栈）由6个编码器（解码器组成）

  • 将 这个编码器和解码器进行放大，我们可以得到：

  • self-attention（multi-head）（多头自注意力机制，Multi-Head Attention）

  • feed forward（前馈神经网络）

  • Add & Norm（加和与归一化，一种常见的残差连接操作）

    • “Add” 表示直接将输入与输出相加，避免输入信息在网络中消失

    • “Norm” 则表示针对相加后的结果进行标准化（归一化）操作，可以保持梯度的稳定性，促进网络收敛

  1. 工作的大体流程

    概念：

    Embedding：将输入的离散化表示（如单词、字符等）映射为实数向量（即连续的空间）表示，作为原始数据的 Feature。在Transformer模型中，通过一个线性变换（即矩阵乘法）将输入的离散化表示映射为了连续实数空间的向量表示，这个过程就是embedding

    • 第一步：获取输入句子的每一个单词的表示向量 X，X由单词的 Embedding 和单词位置的 Embedding 相加得到。

    • 第二步：将得到的单词表示向量矩阵 (如上图所示，每一行是一个单词的表示 x) 传入 Encoder 中，得到句子所有单词的编码信息矩阵 C

      单词向量矩阵用 X_{n \times d} 表示， n 是句子中单词个数，d 是表示向量的维度 (论文中 d=512)。每一个 Encoder block 输出的矩阵维度与输入完全一致。如下图：

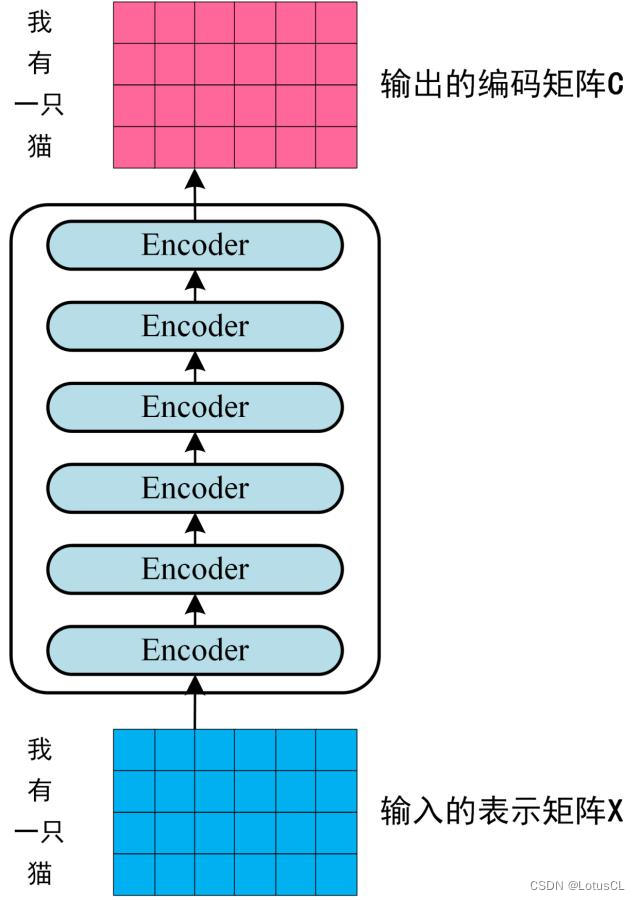
    • 第三步：Encoder 输出的编码信息矩阵 C传递到 Decoder 中，Decoder 依次会根据当前翻译过的单词 1~ i 翻译下一个单词 i+1，如下图所示。在使用的过程中，翻译到单词 i+1 的时候需要通过 Mask (掩盖) 操作遮盖住 i+1 之后的单词。

      上图 Decoder 接收了 Encoder 的编码矩阵 C，然后首先输入一个翻译开始符 "<Begin>"，预测第一个单词 "I"；然后输入翻译开始符 "<Begin>" 和单词 "I"，预测单词 "have"，以此类推。这是 Transformer 使用时候的大致流程

二、Transformer 的输入

前面说过，Transformer 中单词的输入表示 x由单词 Embedding 和位置 Embedding （Positional Encoding）相加得到。

2.1 单词 Embedding

单词的 Embedding 有很多种方式可以获取，例如可以采用 Word2Vec、Glove 等算法预训练得到，也可以在 Transformer 中训练得到。

2.2 位置 Embedding

位置 Embedding 用 PE表示，PE 的维度与单词 Embedding 是一样的。PE 可以通过训练得到，也可以使用某种公式计算得到。在 Transformer 中采用了后者，计算公式如下：


PE_{(pos,2i)} = \sin (pos/10000^{2i/d}) \\ PE_{(pos,2i+1)} = \cos (pos/10000^{2i/d})

其中，pos 表示单词在句子中的位置，d 表示 PE的维度 (与词 Embedding 一样)，2i 表示偶数的维度，2i+1 表示奇数维度 (即 2i≤d, 2i+1≤d)

使用这种公式计算 PE 有以下的好处：

  • 使 PE 能够适应比训练集里面所有句子更长的句子，假设训练集里面最长的句子是有 20 个单词，突然来了一个长度为 21 的句子，则使用公式计算的方法可以计算出第 21 位的 Embedding。

  • 可以让模型容易地计算出相对位置，对于固定长度的间距 k，PE(pos+k) 可以用 PE(pos) 计算得到。因为 Sin(A+B) = Sin(A)Cos(B) + Cos(A)Sin(B), Cos(A+B) = Cos(A)Cos(B) - Sin(A)Sin(B)。

三、Self-Attention（自注意力机制）

  • Multi-Head Attention：由多个 Self-Attention组成。

    • Encoder block 包含一个 Multi-Head Attention

    • Decoder block 包含两个 Multi-Head Attention (其中有一个用到 Masked)

  • Add & Norm：加和与归一化，一种常见的残差连接 Residual Connection 操作

    • “Add” 表示直接将输入与输出相加，避免输入信息在网络中消失，即网络退化

    • “Norm” 则表示针对相加后的结果进行标准化（归一化）操作，可以保持梯度的稳定性，促进网络收敛

3.1 Self-Attention 结构

上图是 Self-Attention 的结构，在计算的时候需要用到矩阵Q(查询),K(键值),V(值)。

  • Self-Attention 输入：输入(单词的表示向量 x 组成的矩阵 X ) 或者上一个 Encoder block 的输出。

  • Q, K, V：通过 Self-Attention 的输入进行线性变换得到。

3.2 Q, K, V 的计算

Self-Attention 的输入用矩阵 X 进行表示，则可以使用线性变阵矩阵WQ, WK, WV计算得到Q, K, V。计算如下图所示，注意 X, Q, K, V 的每一行都表示一个单词。

3.3 Self-Attention 的输出

计算 Self-Attention 的输出公式如下：

\mathrm{Attention} (Q, K, V) = \mathrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V \\ \\ d_k \text{ is the number of columns of the Q,K matrix, i.e. vector dimensions}

  • dk 是 Q，K 矩阵的列数，即向量维度。

首先是Q乘以K的转置：

  • 得到的矩阵行列数都为 n，n 为句子单词数（即图中的1，2，3，4）

  • 此矩阵表示单词之间的 attention 强度

  • 为了防止内积过大，因此除以 dk 的平方根

然后是归一化：

  • 使用 Softmax 计算每一个单词对于其他单词的 attention 系数

  • 这里的 Softmax 是对矩阵的每一行进行 Softmax，即每一行的和都变为 1。

最后和 V 相乘：

备注：

  • Softmax 矩阵的第 1 行表示单词 1 与其他所有单词的 attention 系数

  • 最终单词 1 的输出 Z1 等于所有单词 i 的值 V 根据 attention 系数的比例加在一起得到

如何理解 Q K V？我觉得首先 Q 和 K ，一个是要查找的东西（Q），一个是被查找的东西（K），这样的两个矩阵相乘，首先得到的是要查找的东西对每个被查找的东西的相关程度，而 V 的本源和 K 相同，V就是 K 的价值，有些 K 和 Q 的相关性很高，但他的 V 并不高，因此并不值得关注，而有些 K 的 V 就很高，这样下来，V 就是所有 K 的权重，我们就可以在最后乘上 V 后就能知道什么最值得关注（价值高而且相关性高），这就是注意力机制。

3.4 Multi-Head Attention

Multi-Head Attention 是由多个 Self-Attention 组合形成，结构如下：

  • 实际上，Multi-Head Attention 包含多个 Self-Attention 层

  • 首先将输入X分别传递到 h 个不同的 Self-Attention 中，计算得到 h 个输出矩阵Z

  • 举例：当 h = 8 时，MHA 会输出8个 Z 。

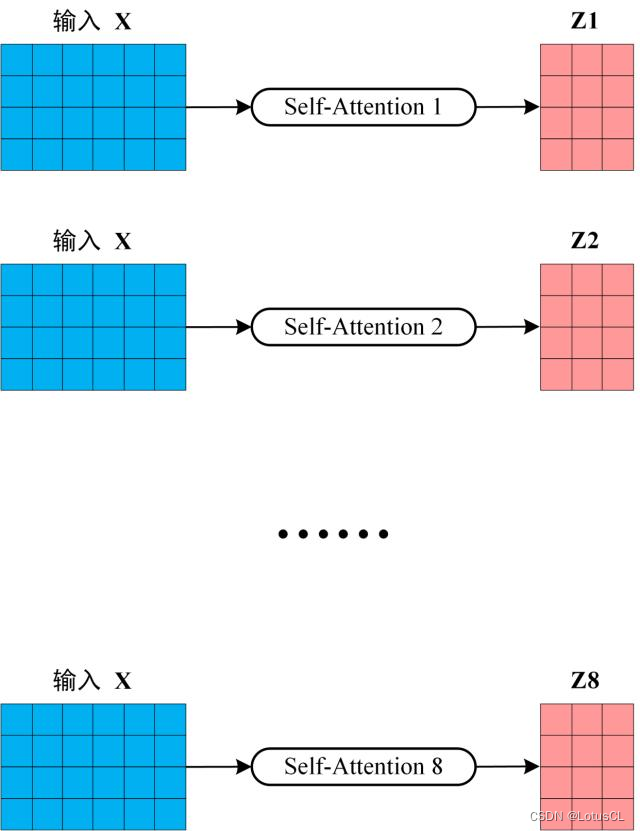
    • Multi-Head Attention 将它们拼接在一起 (Concat)

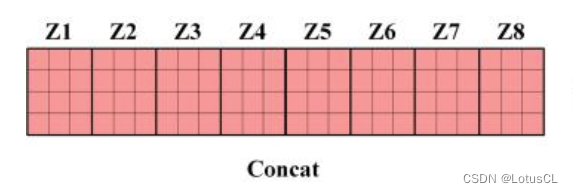
    • 然后传入一个Linear层，得到 Multi-Head Attention 最终的输出Z

    • 这里线性变换后的列数重新变为了输入矩阵的列数。

    • 因此 Multi-Head Attention 输出的矩阵Z与其输入的矩阵X的维度是一样的。

四、Encoder 结构

重新回顾结构，一个Encoder Blocker 由 Add & Norm、Feed Forward、Multi-Head Attention 组成。

4.1 Add & Norm 结构

其计算公式如下：

\mathrm{LayerNorm}(X + \mathrm{MultiHeadAttention}(X)) \\ \mathrm{LayerNorm}(X + \mathrm{FeedForward}(X))

  • X 表示 Multi-Head Attention 或者 Feed Forward 的输入

  • MultiHeadAttention(X) 和 FeedForward(X) 表示输出（输出与输入 X 维度是一样的，所以可以相加）

  1. Add指 X+MultiHeadAttention(X)，是一种残差连接，通常用于解决多层网络训练的问题，可以让网络只关注当前差异的部分，在 ResNet 中经常用到：

  2. Norm指 Layer Normalization，通常用于 RNN 结构，Layer Normalization 会将每一层神经元的输入都转成均值方差都一样的（归一化操作通常包括计算输入的均值和方差，并应用缩放和平移操作，以使其具有标准差是 1，平均值为 0 的分布），这样可以加快收敛。

4.2 Feed Forward

是一个简单的前馈神经网络，公式如下：

\max(0,XW_1 + b_1)W_2 + b_2

  • 一共两层全连接层，第一层激活函数为 Relu，第二层没有激活函数。

    全连接层：将输入数据进行矩阵乘法并加上一个偏置向量，得到输出结果。即 y = Wx + b，W权重矩阵和 b偏置向量通过训练神经网络来确定。

    Relu：当输入张量中元素小于零时，该函数将它们替换为零；否则保持不变。

  • X 是输入，Feed Forward 最终得到的输出矩阵的维度与 X 一致。

4.3 组成 Encoder

  1. Multi-Head Attention, Feed Forward, Add & Norm 就可以构造出一个 Encoder block，Encoder block 接收输入矩阵 X (n*d)，并输出一个矩阵 O (n*d) 。通过多个 Encoder block 叠加就可以组成 Encoder。

  2. 第一个 Encoder block 的输入为句子单词的表示向量矩阵，后续 Encoder block 的输入是前一个 Encoder block 的输出，最后一个 Encoder block 输出的矩阵就是编码信息矩阵 C，这一矩阵后续会用到 Decoder 中。

五、Decoder 结构

  • 包含两个 Multi-Head Attention 层。

  • 第一个 Multi-Head Attention 层采用了 Masked 操作。

  • 第二个 Multi-Head Attention 层的K, V矩阵使用 Encoder 的编码信息矩阵C进行计算，而Q使用上一个 Decoder block 的输出计算。

  • 最后有一个 Softmax 层计算下一个翻译单词的概率。

5.1 第一个 Multi-Head Attention

这里使用了类 Teacher Forcing 的技术。

Teacher Forcing：一种在训练序列生成模型（如语言模型、机器翻译模型等）中常用的技术。在训练过程中，Teacher Forcing 通过将模型的真实目标序列作为输入来辅助模型的训练。

在序列生成任务中，通常采用逐步生成的方法，即每个时间步生成一个输出。在没有 Teacher Forcing 的情况下，模型在每个时间步仅根据前一个时间步的输出进行预测。然而，这种方式容易导致累积误差的积累，尤其是对于较长的序列。

Teacher Forcing 的思想是，在训练过程中，在模型生成的每个时间步，将真实的目标输出作为模型的输入，而不是使用模型自身生成的输出。这样做可以有效地加速模型的收敛，并减少累积错误的影响。通过引入真实目标序列，模型能够更好地学习到正确的输出模式和上下文信息。

然而，需要注意的是，在实际应用中，我们可能无法获得完全正确的目标序列，因此在推断阶段（生成阶段）不使用 Teacher Forcing 是常见的做法。在推断阶段，模型需要依靠自己的预测结果生成输出序列。

Decoder block 的第一个 Multi-Head Attention 采用了 Masked 操作，因为在翻译的过程中是顺序翻译的，即翻译完第 i 个单词，才可以翻译第 i+1 个单词。通过 Masked 操作可以防止第 i 个单词知道 i+1 个单词之后的信息。

而在Decoder 的时候，是需要根据之前的翻译，求解当前最有可能的翻译，如下图所示。首先根据输入 "<Begin>" 预测出第一个单词为 "I"，然后根据输入 "<Begin> I" 预测下一个单词 "have"。

Decoder 可以在训练的过程中使用 Teacher Forcing 并且并行化训练，即将正确的单词序列 (<Begin> I have a cat) 和对应输出 (I have a cat <end>) 传递到 Decoder。那么在预测第 i 个输出时，就要将第 i+1 之后的单词掩盖住，注意：Mask 操作是在 Self-Attention 的 Softmax 之前使用的，下面用 0 1 2 3 4 5 分别表示 "<Begin> I have a cat <end>"。

这里的并行化训练指的是 一句话 直接投入训练当中，而无需与Inference（推断阶段，即使用模型）时所进行的，一个一个输入，相同。下图是在使用模型时的场景，与此时的并行化训练作对比。

  1. 第一步：准备Decoder 的输入矩阵和 Mask 矩阵。

    • 输入矩阵包含 "<Begin> I have a cat" (0, 1, 2, 3, 4) 五个单词的表示向量

    • Mask 是一个 5×5 的矩阵。在 Mask 可以发现单词 0 只能使用单词 0 的信息，而单词 1 可以使用单词 0, 1 的信息，即只能使用之前的信息。

  2. 第二步：通过输入矩阵X计算得到Q,K,V矩阵。然后计算Q和 K^T 的乘积 QK^T 。

  3. 第三步：在得到 QK^T 之后，我们先使用Mask矩阵遮挡住每一个单词之后的信息，得到 Mask QK^T ，然后再进行例行的 Softmax，计算 attention score。遮挡操作如下：

    进行 Softmax 后，每一行的和都为 1。但是单词 0 在单词 1, 2, 3, 4 上的 attention score 都为 0。

  4. 第四步：使用 Mask QK^T 与矩阵 V相乘，得到输出 Z，则单词 1 的输出向量 Z1（即矩阵 Z 的第一行）是只包含单词 1 信息的。

  5. 第五步：通过上述步骤就可以得到一个 Mask Self-Attention 的输出矩阵 Zi ，然后和 Encoder 类似，通过 Multi-Head Attention 拼接多个输出 Zi 然后计算得到第一个 Multi-Head Attention 的输出Z，Z与输入X维度一样。（下方图借用Encoder的讲解图，实际上单词数量（行数）不对）

5.2 第二个 Multi-Head Attention

  • Decoder block 第二个 Multi-Head Attention 变化不大， 主要的区别在于其中 Self-Attention 的 K, V矩阵不是使用 上一个 Decoder block 的输出计算的，而是使用 Encoder 的编码信息矩阵 C 计算的。

  • 根据 Encoder 的输出 C计算得到 K, V，根据上一个 Decoder block 的输出 Z 计算 Q (如果是第一个 Decoder block 则使用输入矩阵 X 进行计算)，后续的计算方法与之前描述的一致。

  • 这样做的好处是在 Decoder 的时候，每一位单词都可以利用到 Encoder 所有单词的信息 (这些信息无需 Mask)。

5.3 Softmax 预测输出单词

多个Decoder block 最终组合成 Decoder。

Decoder 最后的部分是利用 Softmax 预测下一个单词，在之前的网络层我们可以得到一个最终的输出 Z，因为 Mask 的存在，使得单词 0 的输出 Z0 只包含单词 0 的信息，如下：

Softmax 根据输出矩阵的每一行预测下一个单词：

由此构成了一个 Decoder Block。多个 Decoder block 组合成 Decoder。

基于transformer的端到端语音识别模型解析
AI天才研究院
04-08 842
语音识别作为人机交互的重要技术之一,在近年来得到了飞速的发展。传统的语音识别系统通常由声学模型、语言模型和解码器三个主要部分组成,需要进行复杂的管道式处理。随着深度学习技术的不断发展,出现了基于端到端(end-to-end)的语音识别模型,能够直接从原始语音信号中输出文本序列,大大简化了系统结构。其中,基于Transformer的端到端语音识别模型在近年来取得了突破性的进展,在多个公开数据集上取得了领先的识别性能。
自然语言处理基础知识入门(四) Transformer模型整体最详解（self- attention机制，mask机制）
WANGYANG的博客
05-11 1335
在前面的章节中，详细讨论了循环神经网络（RNN）及其衍生模型，经过对RNN的不断改良，它们现在已经具备了长期记忆的能力，这无疑是语言模型领域的一项重大突破。然而，现在的多模态技术以及GPT的出现，绝大多数都选择了基于Transformer的架构，这是为何呢？本章节将围绕这个问题展开，将深入讲解自注意力机制，揭示这个如今在整个自然语言处理领域产生了深远影响的技术的精髓。这将为读者理解后续的BERT模型、GPT技术，以及多模态技术如CLIP等内容奠定坚实的基础。
深度学习笔记——Transformer（上篇）
最新发布
haopinglianlian的博客
02-27 864
本文详细介绍面试过程中可能遇到的Transformer知识点，由于字数限制，分为上下篇发布。
[深度学习概念]·深度学习Transformer模型介绍
热门推荐
简明AI工作室
01-18 1万+
深度学习Transformer模型介绍 转载地址 目录 深度学习Transformer模型介绍 CNN RNN 核心问题 Transformer结构 亮点 self-Attention MultiHead Attention position Encoding 总结一下 动机 常见的seq2seq问...
论文分享 | SpeechFormer: 利用语音信号的层次化特性提升Transformer在认知性语音信号处理领域中的性能
weixin_48827824的博客
10-26 2264
Transformer在认知性语音信号处理（cognitive speech signal processing，CoSSP）领域，包括在情感分析到神经认知障碍分析等各种应用中，都取得了让人瞩目的成绩。然而，目前大部分工作将语音信号视为一个整体进行处理，忽略了语音信号所特有的、能够反映人类认知过程的发音结构。同时，Transformer中全局注意力（full attention）庞大的计算量再实际应用中带来了很大的计算压力。
魔改Transformer！9种提速又提效的模型优化方案
python12345678_的博客
07-04 2387
Transformer目前已经成为人工智能领域的主流模型，应用非常广泛。然而Transformer中注意力机制计算代价较高，随着序列长度的增加，这个计算量还会持续上升。为了解决这个问题，业内出现了许多Transformer的魔改工作，以优化Transformer的运行效率。我这次就给大家。文章主要涉及4个方向：稀疏注意力机制、Transformer处理长文本、Transformer运行提效以及卷积Attention，原文及源码都已整理。
CNN、RNN、LSTM、BiLSTM、Transformer的在EEG信号处理中的作用
sxn0121的博客
06-02 5678
需要注意的是，CNN和RNN并不是相互排斥的，它们可以结合使用，例如在图像字幕生成任务中，可以使用CNN提取图像特征，然后将这些特征输入到RNN中生成描述文字。总之，CNN主要适用于提取EEG信号的时空特征和多通道处理，而RNN主要适用于捕捉EEG信号中的时间依赖关系和序列建模。在实际应用中，CNN和RNN可以结合使用，以充分利用它们各自的优势。CNN（卷积神经网络）和RNN（循环神经网络）是深度学习中常用的两种神经网络结构，它们在处理不同类型的数据和解决不同类型的问题时具有不同的优势。
Transformer模型详解
weixin_49376454的博客
05-28 2169
Transformer模型详解（人工智能）
Transformer细节（四）——详解Transformer解码器的数据处理是并行or顺序
weixin_47129891的博客
06-22 806
在训练阶段，Transformer的解码器利用教师强制方法进行并行计算，因为所有目标序列的真实值都是已知的。而在推理阶段，由于需要逐步生成序列，解码器采用顺序计算方法。这种设计使得模型在训练时具有高效的并行处理能力，而在推理时能够逐步生成准确的输出序列。
Transformer架构详解，一文看懂不是梦！！！
qq_55009448的博客
09-24 4668
在机器翻译应用中，它输入一种语言，通过一个编码组件和一个解码组件后输出对应的另一种语言。输入嵌入（Input Embedding）：输入序列中的每个元素（如单词、图像块等）会先转换为向量表示，通常通过嵌入层进行。位置编码（Positional Encoding）：由于 Transformer 不能像 RNN 那样通过顺序自然感知位置信息，需要添加额外的位置信息。位置编码可以使用正弦和余弦函数，帮助模型感知序列中每个元素的顺序。自注意力层（Self-Attention Layer）
Document-Transformer：使用文档级上下文改进Transformer转换模型
02-25
使用文档级上下文改进变压器翻译模型 内容 介绍 这是我们工作的实现，将Transformer扩展为集成文档级上下文[ ]。 该实现在 用法 注意：用法不是用户友好的。 以后可能会改善。 训练标准的变压器模型，请参考的用户手册。 假设model_baseline / model.ckpt-30000在验证集上表现最佳。 使用以下命令生成虚拟的改进的Transformer模型： python THUMT/thumt/bin/trainer_ctx.py --inputs [source corpus] [target corpus] \ --context [context corpus] \ --vocabulary [source
声音转换——基于深度学习的特征提取方法详解
DuHz的博客
11-08 2521
声音转换技术涉及多种语音特征的处理与转换，包括声道特征（如梅尔频率倒谱系数MFCC）、基频（Pitch）、韵律特征（Prosody）等。传统方法多基于统计模型，如高斯混合模型（GMM）、隐马尔可夫模型（HMM），而深度学习方法则通过构建复杂的神经网络模型，能够更好地捕捉语音特征之间的非线性关系，提高转换效果。基于深度学习的声音转换方法通过构建复杂的神经网络模型，实现源说话者特征到目标说话者特征的高效映射。深度学习方法在特征提取、表示、转换和合成各个环节展现出强大的能力，显著提升了声音转换的自然度和准确性。
深度学习 Transformer机制
Fantastic
10-30 6459
Transformer
Transformer的七十二变！12种魔改的Transformer模型大分享
Everly_的博客
12-19 2800
但正如所有科技的进化，Transformer也在不断地被“魔改”以适应更复杂的任务和挑战。下面我们探讨了几种令人印象深刻的Transformer模型变体，它们通过创新的技术改进，解决了传统Transformer模型在处理长序列、计算效率和内存使用等方面的局限性。稀疏注意力机制在Transformer中通过减少不必要的计算，降低模型的计算复杂度和内存需求，使得模型能够更高效地处理长序列数据，同时保持或提升模型性能。1.1动态稀疏注意力（DSA）
Transformer 的结构改进与替代方案
hellozhxy的博客
03-09 3644
自从 Transformer 结构被提出以来，以 BERT 为代表的 Encoder 模型，以 GPT 为代表的 Decoder 模型，以 ViT 为代表的 CV 模型，都烜赫一时。时至今日，几乎所有的 LLM 也都是 Transformer 结构，尽管不时也会有新的结构被提出来，但 Transformer 的江湖地位仍然无可撼动。希望通过以上问题的思考和讨论，能够帮助我们更好地使用Transformer、理解Transformer、优化Transformer和改进Transformer。
【语音信号处理】2语音信号实践——LSTM(hidden、output)、Attention、语音可视化
YoungSeng's Blog
04-16 1735
语音 关于class torch.utils.data.Dataset官方文档，
Transformer模型在语音识别和语音生成中的应用
AI天才研究院
01-08 1806
1.背景介绍 语音识别和语音生成是人工智能领域的两个重要研究方向，它们在现实生活中的应用也非常广泛。语音识别技术可以将语音信号转换为文本，从而实现人机交互、语音助手等功能；而语音生成技术则可以将文本转换为语音，实现文字到语音的转换，从而提供语音新闻、导航等服务。 在过去的几年里，深度学习技术呈现了快速发展的趋势，尤其是自然语言处理(NLP)领域的成果，如机器翻译、情感分析等，都取得了显著的进展...
【计算机视觉 | Transformer】魔改Transformer！9种提速又提效的模型优化方案分享！
wzk4869的博客
11-30 5097
【计算机视觉 | Transformer】魔改Transformer！9种提速又提效的模型优化方案分享！
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值