《深入浅出通信原理》03

1. 周期信号的离散谱

构成周期信号的所有复指数信号成分可以用傅里叶系数来描述，但是傅里叶系数不够直观，有没有什么办法可以把傅里叶系数直观地呈现出来呢？这就引出了频谱。

1.1 幅度谱

以频率为横轴，以幅度为纵轴，将所有ck的幅度（也就是模）画到一张图中，这就是幅度谱。周期为1s的方波信号幅度谱如下图所示。

周期为1s的方波信号幅度谱

1.2 相位谱

以频率为横轴，以初相为纵轴，将所有ck的初相画到一张图中，这就是相位谱。周期为1s的方波信号相位谱如下图所示。

周期为1s的方波信号相位谱

举个大家更熟悉的例子：正弦信号

正弦信号的幅度谱

正弦信号的相位谱

 也就是说对于用傅里叶技术展开的周期信号来说，幅度谱是画出对应频率下傅里叶系数的模值，而相位谱是画出对应频率下傅里叶系数的相角。

2. 非周期信号的连续谱

非周期信号的连续谱推导

• 以T为周期，对非周期信号x(t)进行周期性拓展得到周期信号xT(t)。
• 求出周期信号xT(t)的傅里叶系数。

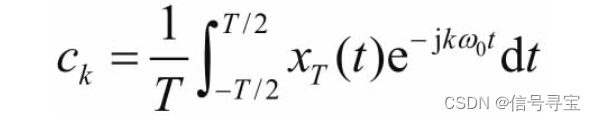
• 将T=1/f0，ω0=2πf0代入得

•  由ck求ck/f0

• T趋于无穷大时，f0趋于0，ck/f0演变为X(f)，xT(t)演变为x(t)，kf0演变为f，由此得到非周期信号x(t)的连续谱

 这个式子就是非周期函数的连续谱的表达式，也就是傅里叶变换。也就是说，我们常说的傅里叶变换是为了解决如何得到非周期函数的频谱这一问题的。而这里的频谱和周期函数的离散频谱不一样，这里的频谱是密度谱。

其实傅里叶逆变换也可以用这样的方式推导，有兴趣的小伙伴可以对照下面这个步骤图试一下，我这里就直接给出傅里叶逆变换的公式了。

由连续谱求对应非周期信号的方法

傅里叶逆变换

 我们这里把傅里叶正变换的公式也写过来

傅里叶正变换

 傅里叶正变换和逆变换统称傅里叶变换。上面的傅里叶变换表达式中使用的变量是f，有时候傅里叶变换表达式也使用ω作为变量。由ω=2πf，得到：f=ω/2π，代入上面的傅里叶变换表达式，很容易得到变量为ω的傅里叶变换表达式。

傅里叶正变换

傅里叶逆变换

 3. 周期信号的傅里叶变换

根据傅里叶级数展开，周期信号可以分解为一系列复指数信号之和：

傅里叶级数

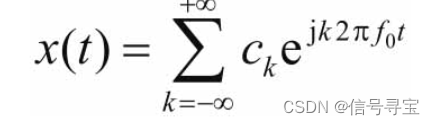
根据傅里叶变换的定义：

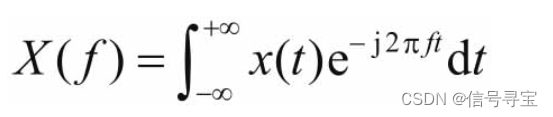
 求得

也就是说，周期信号的傅里叶变换是由一系列的冲激函数构成，这些冲激位于信号的基波和各谐波频率处，冲激的强度是傅里叶系数ck。