《大话数据结构》13 拓扑排序和关键路径

1. 拓扑排序

我们会把施工过程、生产流程、软件开发、教学安排等都当成一个项目工程来对待，所有的工程都可分为若干个“活动”的子工程。例如下图是我这非专业人士绘制的一张电影制作流程图，现实中可能并不完全相同，但基本表达了一个工程和若干个活动的概念。在这些活动之间，通常会受到一定的条件约束，如其中某些活动必须在另一些活动完成之后才能开始。就像电影制作不可能在人员到位进驻场地时，导演还没有找到，也不可能在拍摄过程中，场地都没有。这都会导致荒谬的结果。因此这样的工程图，一定是无环的有向图。

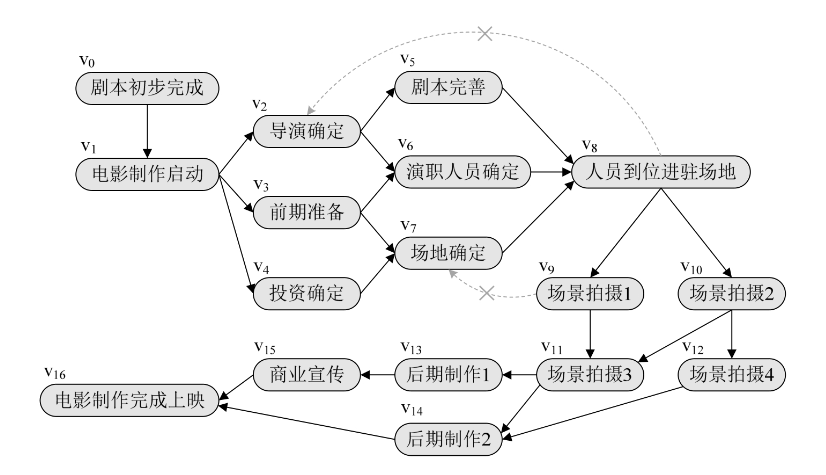
在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们称为AOV网（Activity On Vertex Network）。 AOV网中的弧表示活动之间存在的某种制约关系。比如演职人员确定了，场地也联系好了，才可以开始进场拍摄。另外就是AOV网中不能存在回路。刚才已经举了例子，让某个活动的开始要以自己完成作为先决条件，显然是不可以的。

设G=(V,E)是一个具有n个顶点的有向图，V中的顶点序列v1，v2，……，vn，满足若从顶点vi到vj有一条路径，则在顶点序列中顶点vi必在顶点vj之前。则我们称这样的顶点序列为一个拓扑序列。

上图这样的AOV网的拓扑序列不止一条。序列v0 v1 v2 v3 v4 v5 v6 v7 v8 v9v10 v11 v12 v13 v14 v15 v16是一条拓扑序列，而v0 v1 v4 v3 v2 v7 v6 v5 v8v10 v9 v12 v11 v14 v13 v15 v16也是一条拓扑序列。

所谓拓扑排序，其实就是对一个有向图构造拓扑序列的过程。构造时会有两个结果，如果此网的全部顶点都被输出，则说明它是不存在环（回路）的AOV网；如果输出顶点数少了，哪怕是少了一个，也说明这个网存在环（回路），不是AOV网。

一个不存在回路的AOV网，我们可以将它应用在各种各样的工程或项目的流程图中，满足各种应用场景的需要，所以实现拓扑排序的算法就很有价值了。

2. 拓扑排序算法

对AOV网进行拓扑排序的基本思路是：从AOV网中选择一个入度为0的顶点输出，然后删去此顶点，并删除以此顶点为尾的弧，继续重复此步骤，直到输出全部顶点或者AOV网中不存在入度为0的顶点为止。

首先我们需要确定一下这个图需要使用的数据结构。前面求最小生成树和最短路径时，我们用的都是邻接矩阵，但由于拓扑排序的过程中，需要删除顶点，显然用邻接表会更加方便。因此我们需要为AOV网建立一个邻接表。考虑到算法过程中始终要查找入度为0的顶点，我们在原来顶点表结点结构中，增加一个入度域in，结构如下表所示，其中in就是入度的数字。

因此对于下图的第一幅图AOV网，我们可以得到如第二幅图的邻接表数据结构。 

在拓扑排序算法中，涉及的结构代码如下。

在算法中，我还需要辅助的数据结构—栈，用来存储处理过程中入度为0的顶点，目的是为了避免每个查找时都要去遍历顶点表找有没有入度为0的顶点。

现在我们来看代码，并且模拟运行它。

 1．程序开始运行，第3～7行都是变量的定义，其中stack是一个栈，用来存储整型的数字。

2．第8～10行，作了一个循环判断，把入度为0的顶点下标都入栈，从下图的右图邻接表可知，此时stack应该为：{0，1，3}，即v0、v1、v3的顶点入度为0，如下图所示。

3．第12～23行，while循环，当栈中有数据元素时，始终循环。

4．第14～16行，v3出栈得到gettop=3。并打印此顶点，然后count加1。

5．第17～22行，循环其实是对v3顶点对应的弧链表进行遍历，即下图中的灰色部分，找到v3连接的两个顶点v2和v13，并将它们的入度减少一位，此时v2和v13的in值都为1。它的目的是为了将v3顶点上的弧删除。 

6．再次循环，第12～23行。此时处理的是顶点v1。经过出栈、打印、count=2后，我们对v1到v2、v4、v8的弧进行了遍历。并同样减少了它们的入度数，此时v2入度为0，于是由第20～21行知，v2入栈，如下图所示。试想，如果没有在顶点表中加入in这个入度数据域，20行的判断就必须要是循环，这显然是要消耗时间的，我们利用空间换取了时间。 

7．接下来，就是同样的处理方式了。下图展示了v2 v6 v0 v4 v5 v8的打印删除过程，后面还剩几个顶点都类似，就不图示了。 

8．最终拓扑排序打印结果为3->1->2->6->0->4->5->8->7->12->9->10->13->11。当然这结果并不是唯一的一种拓扑排序方案。

分析整个算法，对一个具有n个顶点e条弧的AOV网来说，第8～10行扫描顶点表，将入度为0的顶点入栈的时间复杂为O(n)，而之后的while循环中，每个顶点进一次栈，出一次栈，入度减1的操作共执行了e次，所以整个算法的时间复杂度为O(n+e)。

3. 关键路径

 拓扑排序主要是为解决一个工程能否顺序进行的问题，但有时我们还需要解决工程完成需要的最短时间问题。比如说，造一辆汽车，我们需要先造各种各样的零件、部件，最终再组装成车，如下图所示。这些零部件基本都是在流水线上同时生产的，假如造一个轮子需要0.5天时间，造一个发动机需要3天时间，造一个车底盘需要2天时间，造一个外壳需要2天时间，其他零部件时间需要2天，全部零部件集中到一处需要0.5天，组装成车需要2天时间，请问，在汽车厂造一辆车，最短需要多少时间呢？

有人说时间就是全部加起来，这当然是不对的。我已经说了前提，这些零部件都是分别在流水线上同时生产的，也就是说，在生产发动机的3天里，可能已经生产了6个轮子，1.5个外壳和1.5个底盘，而组装车是在这些零部件都生产好后才可以进行。因此最短的时间其实是零部件中生产时间最长的发动机3天+集中零部件0.5天+组装车的2天，一共5.5天完成一辆汽车的生产。因此，我们如果要对一个流程图获得最短时间，就必须要分析它们的拓扑关系，并且找到当中最关键的流程，这个流程的时间就是最短时间。

因此在前面讲了AOV网的基础上，我们来介绍一个新的概念。在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，用边上的权值表示活动的持续时间，这种有向图的边表示活动的网，我们称之为AOE网（Activity On Edge Network）。 

我们把AOE网中没有入边的顶点称为始点或源点，没有出边的顶点称为终点或汇点。由于一个工程，总有一个开始，一个结束，所以正常情况下，AOE网只有一个源点一个汇点。例如下图就是一个AOE网。其中v0即是源点，表示一个工程的开始，v9是汇点，表示整个工程的结束，顶点v0，v1，……，v9分别表示事件，弧<v0,v1>，<v0,v2>，……，<v8,v9>都表示一个活动，用a0，a1，……，a12表示，它们的值代表着活动持续的时间，比如弧<v0,v1>就是从源点开始的第一个活动a0，它的时间是3个单位。

既然AOE网是表示工程流程的，所以它就具有明显的工程的特性。如有在某顶点所代表的事件发生后，从该顶点出发的各活动才能开始。只有在进入某顶点的各活动都已经结束，该顶点所代表的事件才能发生。

尽管AOE网与AOV网都是用来对工程建模的，但它们还是有很大的不同，主要体现在AOV网是顶点表示活动的网，，它只描述活动之间的制约关系，而AOE网是用边表示活动的网，边上的权值表示活动持续的时间，如下图所示两图的对比。因此，AOE网是要建立在活动之间制约关系没有矛盾的基础之上，再来分析完成整个工程至少需要多少时间，或者为缩短完成工程所需时间，应当加快哪些活动等问题。 

我们把路径上各个活动所持续的时间之和称为路径长度，从源点到汇点具有最大长度的路径叫关键路径，在关键路径上的活动叫关键活动。显然就下图的AOE网而言，开始→发动机完成→部件集中到位→组装完成就是关键路径，路径长度为5.5。 

如果我们需要缩短整个工期，去改进轮子的生产效率，哪怕改动成0.1也是无益于整个工期的变化，只有缩短关键路径上的关键活动时间才可以减少整个工期长度。例如如果发动机制造缩短为2.5，整车组装缩短为1.5，那么关键路径长度就为4.5，整整缩短了一天的时间。

那么现在的问题就是如何找出关键路径。

3.1 关键路径算法原理

为了讲清楚求关键路径的算法，我还是来举个例子。假设一个学生放学回家，除掉吃饭、洗漱外，到睡觉前有四小时空闲，而家庭作业需要两小时完成。不同的学生会有不同的做法，抓紧的学生，会在头两小时就完成作业，然后看看电视、读读课外书什么的；但也有超过一半的学生会在最后两小时才去做作业，要不是因为没时间，可能还要再拖延下去。下面的同学不要笑，像是在说你的是吧，你们是不是有过暑假两个月，要到最后几天才去赶作业的坏毛病呀？这也没什么好奇怪的，拖延就是人性几大弱点之一。

这里做家庭作业这一活动的最早开始时间是四小时的开始，可以理解为0，而最晚开始时间是两小时之后马上开始，不可以再晚，否则就是延迟了，此时可以理解为2。显然，当最早和最晚开始时间不相等时就意味着有空闲。

接着，你老妈发现了你拖延的小秘密，于是买了很多的课外习题，要求你四个小时，不许有一丝空闲，省得你拖延或偷懒。此时整个四小时全部被占满，最早开始时间和最晚开始时间都是0，因此它就是关键活动了。

也就是说，我们只需要找到所有活动的最早开始时间和最晚开始时间，并且比较它们，如果相等就意味着此活动是关键活动，活动间的路径为关键路径。如果不等，则就不是。

为此，我们需要定义如下几个参数。

1．事件的最早发生时间etv（earliest time of vertex）：即顶点vk的最早发生时间。

2．事件的最晚发生时间ltv（latest time of vertex）：即顶点vk的最晚发生时间，也就是每个顶点对应的事件最晚需要开始的时间，超出此时间将会延误整个工期。

3．活动的最早开工时间ete（earliest time of edge）：即弧ak的最早发生时间。

4．活动的最晚开工时间lte（latest time of edge）：即弧ak的最晚发生时间，也就是不推迟工期的最晚开工时间。

我们是由1和2可以求得3和4，然后再根据ete[k]是否与lte[k]相等来判断ak是否是关键活动。

3.2 关键路径算法

我们还是用之前的例子，注意与拓扑排序时邻接表结构不同的地方在于，这里弧链表增加了weight域，用来存储弧的权值。

求事件的最早发生时间etv的过程，就是我们从头至尾找拓扑序列的过程，因此，在求关键路径之前，需要先调用一次拓扑序列算法的代码来计算etv和拓扑序列列表。为此，我们首先在程序开始处声明几个全局变量。

其中stack2用来存储拓扑序列，以便后面求关键路径时使用。

下面是改进过的求拓扑序列算法。

代码中，除加粗部分外，与前面讲的拓扑排序算法没有什么不同。

第11～15行为初始化全局变量etv数组、top2和stack2的过程。第21行就是将本是要输出的拓扑序列压入全局栈stack2中。第27～28行很关键，它是求etv数组的每一个元素的值。比如说，假如我们已经求得顶点v0对应的etv[0]=0，顶点v1对应的etv[1]=3，顶点v2对应的etv[2]=4，现在我们需要求顶点v3对应的etv[3]，其实就是求etv[1]+len<v1,v3>与etv[2]+len<v2,v3>的较大值。显然3+5<4+8，得到etv[3]=12，如下图所示。在代码中e->weight就是当前弧的长度。

 由此我们也可以得出计算顶点vk即求etv[k]的最早发生时间的公式是：

其中P[K]表示所有到达顶点vk的弧的集合。比如上图的P[3]就是<v1,v3>和<v2,v3>两条弧。len<vi,vk>是弧<vi,vk>上的权值。 

下面我们来看求关键路径的算法代码。

1．程序开始执行。第5行，声明了ete和lte两个活动最早最晚发生时间变量。

2．第6行，调用求拓扑序列的函数。执行完毕后，全局变量数组etv和栈stack的值如下图所示，top2=10。也就是说，对于每个事件的最早发生时间，我们已经计算出来了。

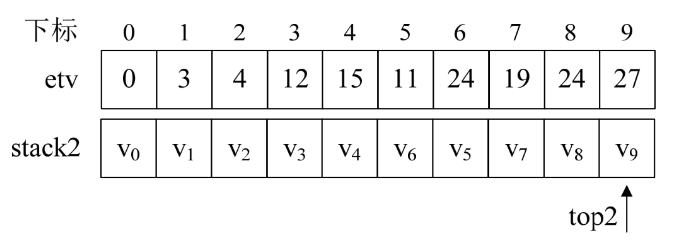
3．第7～9行为初始化全局变量ltv数组，因为etv[9]=27，所以数组ltv当前的值为：{27，27，27，27，27，27，27，27，27，27}

4．第10～19行为计算ltv的循环。第12行，先将stack2的栈头出栈，由后进先出得到gettop=9。根据邻接表中，v9没有弧表，所以第13～18行循环体未执行。 

5．再次来到第12行，gettop=8，在第13～18行的循环中，v8的弧表只有一条<v8,v9>，第15行得到k=9，因为ltv[9]－3<ltv[8]，所以ltv[8]=ltv[9]－3=24，如下图所示。

6．再次循环，当gettop=7、5、6时，同理可算出ltv相对应的值为19、25、13，此时ltv值为：{27，27，27，27，27，13，25，19，24，27}

7．当gettop=4时，由邻接表可得到v4有两条弧<v4,v6>、<v4,v7>，通过第13～18行的循环，可以得到ltv[4]=min(ltv[7]－4,ltv[6]－9)=min(19－4,25－9)=15，如下图所示。 

此时你应该发现，我们在计算ltv时，其实是把拓扑序列倒过来进行的。因此我们可以得出计算顶点vk即求ltv[k]的最晚发生时间的公式是：

 

其中S[K]表示所有从顶点vk出发的弧的集合。比如下图的S[4]就是<v4,v6>和<v4,v7>两条弧，en<vk,vj>是弧<vk,vj>上的权值。 

就这样，当程序执行到第20行时，相关变量的值如下图所示，比如etv[1]=3而ltv[1]=7，表示的意思就是如果时间单位是天的话，哪怕v1这个事件在第7天才开始，也可以保证整个工程的按期完成，你可以提前v1事件开始时间，但你最早也只能在第3天开始。跟我们前面举的例子，是先完成作业再玩还是先玩最后完成作业一个道理。

8．第20～31行是来求另两个变量活动最早开始时间ete和活动最晚开始时间lte，并对相同下标的它们做比较。两重循环嵌套是对邻接表的顶点和每个顶点的弧表遍历。

9．当j=0时，从v0点开始，有<v0,v2>和<v0,v1>两条弧。当k=2时，ete=etv[j]=etv[0]=0。lte=ltv[k]-e->weight=ltv[2]-len<v0,v2>=4－4=0，此时ete=lte，表示弧<v0,v2>是关键活动，因此打印。当k=1时，ete=etv[j]=etv[0]=0。lte=ltv[k]-e->weight=ltv[1]-len<v0,v1>=7－3=4，此时ete ≠lte，因此<v0,v1>并不是关键活动，如下图所示。

这里需要解释一下，ete本来是表示活动<vk,vj>的最早开工时间，是针对弧来说的。但只有此弧的弧尾顶点vk的事件发生了，它才可以开始，因此ete=etv[k]。

这里需要解释一下，ete本来是表示活动<vk,vj>的最早开工时间，是针对弧来说的。但只有此弧的弧尾顶点vk的事件发生了，它才可以开始，因此ete=etv[k]。

而lte表示的是活动<vk,vj>的最晚开工时间，但此活动再晚也不能等vj事件发生才开始，而必须要在vj事件之前发生，所以lte=ltv[j]-len<vk,vj>。就像你晚上23点睡觉，你不能说到23点才开始做作业，而必须要提前2小时，在21点开始，才有可能按时完成作业。

所以最终，其实就是判断ete与lte是否相等，相等意味着活动没有任何空闲，是关键活动，否则就不是。

10．j=1一直到j=9为止，做法是完全相同的，关键路径打印结果为“<v0,v2> 4,<v2,v3> 8, <v3,v4> 3, <v4,v7> 4, <v7,v8> 5, <v8,v9> 3,”，最终关键路径如下图所示。

分析整个求关键路径的算法，第6行是拓扑排序，时间复杂度为O(n+e)，第8～9行时间复杂度为O(n)，第10～19行时间复杂度为O(n+e)，第20～31行时间复杂也为O(n+e)，根据我们对时间复杂度的定义，所有的常数系数可以忽略，所以最终求关键路径算法的时间复杂度依然是O(n+e)。

实践证明，通过这样的算法对于工程的前期工期估算和中期的计划调整都有很大的帮助。不过注意，本例是唯一一条关键路径，这并不等于不存在多条关键路径的有向无环图。如果是多条关键路径，则单是提高一条关键路径上的关键活动的速度并不能导致整个工程缩短工期，而必须提高同时在几条关键路径上的活动的速度。这就像仅仅是有事业的成功，而没有健康的身体以及快乐的生活，是根本谈不上幸福的人生一样，三者缺一不可。

4. 总结

在图的讲解中，我们用了三个章节 11，12，13。现在我们来回顾以下

图是.计算机科学中非常常用的一类数据结构，有许许多多的计算问题都是用图来定义的。由于图也是最复杂的数据结构，对它讲解时，涉及到数组、链表、栈、队列、树等之前学的几乎所有数据结构。因此从某种角度来说，学好了图，基本就等于理解了数据结构这门课的精神。

我们在图的定义这一节，介绍了一大堆定义和术语，一开始可能会有些迷茫，不过一回生二回熟，多读几遍，基本都可以理解并记住它们的特征，在图的定义这一节的末尾，我们已经有所总结，这里就不再赘述了。

图的存储结构我们一共讲了五种，如下图所示，其中比较重要的是邻接矩阵和邻接表，它们分别代表着边集是用数组还是链表的方式存储。十字链表是邻接矩阵的一种升级，而邻接多重表则是邻接表的升级。边集数组更多考虑的是对边的关注。用什么存储结构需要具体问题具体分析，通常稠密图，或读存数据较多，结构修改较少的图，用邻接矩阵要更合适，反之则应该考虑邻接表。

图的遍历分为深度和广度两种，各有优缺点，就像人在追求卓越时，是着重深度还是看重广度，总是很难说得清楚。

图的应用是我们这一章浓墨重彩的一部分，一共谈了三种应用：最小生成树、最短路径和有向无环图的应用。

最小生成树，我们讲了两种算法：普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。普里姆算法像是走一步看一步的思维方式，逐步生成最小生成树。而克鲁斯卡尔算法则更有全局意识，直接从图中最短权值的边入手，找寻最后的答案。

最短路径的现实应用非常多，我们也介绍了两种算法。迪杰斯特拉（Dijkstra）算法更强调单源顶点查找路径的方式，比较符合我们正常的思路，容易理解原理，但算法代码相对复杂。而弗洛伊德（Floyd）算法则完全抛开了单点的局限思维方式，巧妙地应用矩阵的变换，用最清爽的代码实现了多顶点间最短路径求解的方案，原理理解有难度，但算法编写很简洁。

有向无环图时常应用于工程规划中，对于整个工程或系统来说，我们一方面关心的是工程能否顺利进行的问题，通过拓扑排序的方式，我们可以有效地分析出一个有向图是否存在环，如果不存在，那它的拓扑序列是什么？另一方面关心的是整个工程完成所必须的最短时间问题，利用求关键路径的算法，可以得到最短完成工程的工期以及关键的活动有哪些。

事实上，图的应用算法还有不少，本章节只是抛砖引玉，有兴趣的同学可以去查阅相关的书籍获得更多的知识。