如何简单快速地计算FIFO的最小深度？

原创 于 2024-08-31 13:25:27 发布 · 959 阅读 · 10 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#嵌入式硬件

如何简单快速地计算FIFO的最小深度？（笔面试常客）_fifo 0.3平方毫米-CSDN博客

1、为什么需要计算FIFO的最小深度

        因为笔试常考。

        开玩笑的。首先我们来想下FIFO有哪些作用？我大概总结下FIFO的几个重要作用：

  • 解决不同时钟域传输的问题
  • 用来缓存一定量的数据
  • 解决位宽不匹配的问题

        FIFO最常被用来解决写、读不匹配的问题（时钟、位宽），总结下来，其实FIFO最大的作用就是缓冲。既然是缓冲，那么就要知道这个缓存的空间到底需要多大。接下来的讨论，都建立在满足一次FIFO突发传输的基础上。连续无止境的突发不考虑。比如写时钟100M，读时钟50M，无限制的读写，那么FIFO的深度只能是无穷大了，因为写比读快，FIFO一定永远都不够用。所以在实际运用中，不会存在无限制的对FIFO进行读写。如果这样的话，FIFO就变成了一个“存储器件”，而不是一个“缓存器件”，对于FIFO的这种用法无疑是毫无意义的。

2、实例

2.1、写时钟快、读时钟慢

2.1.1、无间断的写、读操作

        条件：

                写入时钟频率 fA = 80MHz；读取时钟频率 fB = 50MHz. 一次写入的突发长度120

                读写操作不间断

        解法：

                写入一个数据需要的时间：1/80MHz = 12.5ns；读取一个数据需要的时间：1/50MHz = 20ns

                写入120个数据，需要的时间：120 * 12.5ns = 1500ns

                在写入全部数据所需的时间（1500ns）内，可以读取出的数据数：1500ns / 20ns = 75

                所以一次突发，一共需要写入120数据，在这段时间内可以被读出75数据，剩下的数据就是需要使用FIFO来缓存，所以FIFO的最小深度为120 - 75 = 45

2.1.2、间断的写、读操作

        条件：

                写入时钟频率 fA = 80MHz；读取时钟频率 fB = 50MHz. 一次写入的突发长度120。

                每两次写入操作间隔1个写时钟周期，每两次读取操作间隔3个读时钟周期。

        解法：

                每两次写入操作间隔1个写时钟周期，等于每两个写时钟周期才写入1个数据，即等价的写入时钟频率 fA'=40MHz，写入一个数据需要的时间：1/40MHz = 25ns

                每两次读取操作间隔3个读时钟周期，等于每4个写时钟周期才读取1个数据，即等价的读取时钟频率 fB'=12.5MHz，读取一个数据需要的时间：1/12.5MHz = 80ns

                写入120个数据，需要的时间：120 * 25ns = 3000ns

                在写入全部数据所需的时间（3000ns）内，可以读取出的数据数：3000ns / 80ns = 37.5 ≈ 37（要向下取整，不然有1个数据会丢）

                所以一次突发，一共需要写入120数据，在这段时间内可以被读出37数据，剩下的数据就是需要使用FIFO来缓存，所以FIFO的最小深度为120 - 37 = 83

2.2、写时钟慢、读时钟快

2.2.1、无间断的写、读操作

        条件：

                写入时钟频率 fA = 30MHz；读取时钟频率 fB = 50MHz. 一次写入的突发长度120

                写、读操作无间断

        解法：

                因为读操作的频率快于写操作的频率，所以数据一旦被写入FIFO后很快就会被读走，所以FIFO的最小深度为1即可

2.2.2、间断的写、读操作

        条件：

                写入时钟频率 fA = 30MHz；读取时钟频率 fB = 50MHz. 一次写入的突发长度120。

                每两次写入操作间隔1个写时钟周期，每两次读取操作间隔3个读时钟周期。

        解法：

                每两次写入操作间隔1个写时钟周期，等于每两个写时钟周期才写入1个数据，即等价的写入时钟频率 fA'=15MHz，写入一个数据需要的时间：1/15MHz = 66.667ns

                每两次读取操作间隔3个读时钟周期，等于每4个写时钟周期才读取1个数据，即等价的读取时钟频率 fB'=12.5MHz，读取一个数据需要的时间：1/12.5MHz = 80ns

                 写入120个数据，需要的时间：120 * 66.667ns = 8000ns

                在写入全部数据所需的时间（8000ns）内，可以读取出的数据数：8000ns / 80ns = 100

                所以一次突发，一共需要写入120数据，在这段时间内可以被读出100数据，剩下的数据就是需要使用FIFO来缓存，所以FIFO的最小深度为120 - 100 = 20

2.3、写时钟、读时钟一样快

2.3.1、无间断的写、读操作

        条件：

                写入时钟频率 fA = 读取时钟频率 fB = 30MHz。一次写入的突发长度120。

                写、读操作无间断

        解法：

                1、假设读、写时钟无位差、则两个时钟同频、同相，是同步信号，故可以直接对接操作，无需FIFO

                2、若读、写时钟存在相位差，则被写入的数据在一个时钟周期内会被读走，所以FIFO的最小深度为1即可

2.3.2、间断的写、读操作

        条件：

                写入时钟频率 fA = 读取时钟频率 fB = 50MHz。一次写入的突发长度120。

                每两次写入操作间隔1个时钟周期，每两次读取操作间隔3个时钟周期。

        解法：

                每两次写入操作间隔1个写时钟周期，等于每两个写时钟周期才写入1个数据，即等价的写入时钟频率 fA'=25MHz，写入一个数据需要的时间：1/25MHz = 40ns

                每两次读取操作间隔3个读时钟周期，等于每4个写时钟周期才读取1个数据，即等价的读取时钟频率 fB'=12.5MHz，读取一个数据需要的时间：1/12.5MHz = 80ns

                写入120个数据，需要的时间：120 * 40ns = 4800ns

                在写入全部数据所需的时间（4800ns）内，可以读取出的数据数：4800ns / 80ns = 60

                所以一次突发，一共需要写入120数据，在这段时间内可以被读出60数据，剩下的数据就是需要使用FIFO来缓存，所以FIFO的最小深度为120 - 60 = 60

2.4、特定时间内时间写、读速率固定

        条件：

                每100个时钟写入80个数据，剩余20个随机值（无效）

                每10个时钟读出8个数据

                一次写入的突发长度160

        解法：

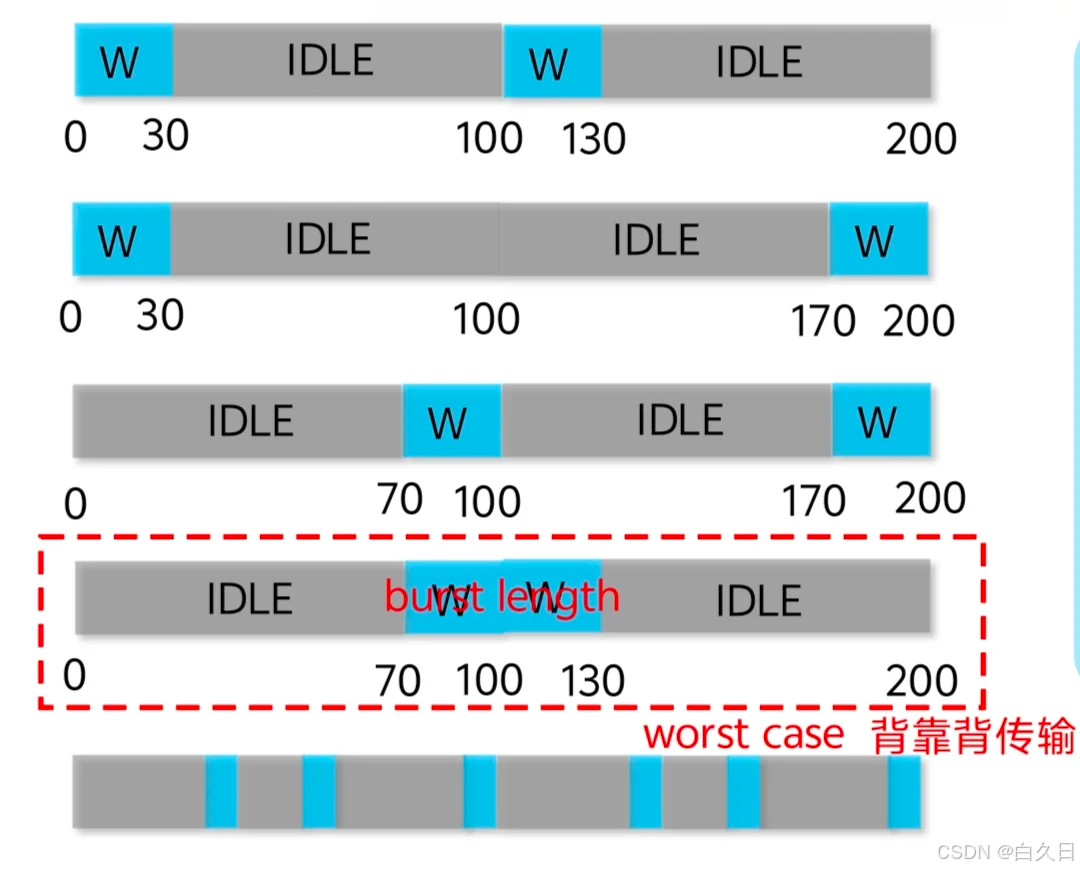
                因为每100个时钟内，仅写入80个数据，而这80个数据可能任意分布，所以160个数据的写入可能有以下几种情况：

        可以看到，第4种情况是最极端的：一次性需要写入160数据，时间为160个时钟

        160个时钟内，读出的数据是160*8/10 = 128

        所以一共需要写入160数据，在这段时间内可以被读出128数据，剩下的数据就是需要使用FIFO来缓存，所以FIFO的最小深度为160 - 128 = 32

3、总结

  • FIFO是用来缓存的，不是用来存数据的，当写快读慢时，无止境的对FIFO操作是没有意义的（不管FIFO多大，一定都会被写满） 
  • FIFO深度的计算建立在满足一次突发传输的基础上
  • 当读快写满或者读写一样快时，FIFO的深度最多只需要1
  • 当写快读慢时，在一次突发传输时，因为读慢，所以肯定无法全部读走。全部写入的数据量 - 已经被读走的数据量 = 需要缓存到FIFO的数据量，即异步FIFO的最小深度

芯片工程师的日常|FIFO最小深度计算 - 小红书

FPGA进阶-计算FIFO最小深度？
whm128的博客
04-27 292
考虑最大数据情况，考虑写数据的连续200个时钟周期，前一个100个时钟记作TimeA，后一个记作TimeB,写数据的恰好在TimeA的最后和TimeB的最前，即20个时钟周期发生连续的20次写，而对应的20个时钟周期会读出2个数据，所以这里需要的最小深度为20-2=18。设计一个同步fifo，读写时钟相同，其中在写入时每100个时钟周期会写10个，具体哪个时刻写入不确定，在读出侧每10个cycle会读1个，计算最小深度？
FIFO最小深度计算
Crazzy_M的博客
07-23 5410
FIFO最小深度计算 文章目录1、FIFO最小深度2、示例分析 1、FIFO最小深度   在数据的传输中当读速率慢于写速率时，FIFO便可被用作系统中的缓冲元件或队列，类似于水流经过一个缓冲区，上游水流速度快，下游水流速度慢，部分水就可以被缓存在中间的缓冲区，但是上游与下游的水速差距过大，就会导致流入中间缓存区的水超出了缓存区承受能力导致水的溢出，不能顺利到达下游。在上游水流速度最大，下游水流速度最小的情况下，中间缓冲区不能溢出的大小就是我们关系的问题。   同理，读写速率差距过大，FIFO深度太小，就
FIFO深度计算
little_ox的博客
07-08 6630
FIFO深度学习 格雷码的轴对称问题。这个我在学格雷码的时候还真没想到。 2，为何用格雷码而非二进制码做CDC。 3，异步FIFO的大致框图。 4，满空信号产生。尤其是满。 5，RDCLK和WRCLK差距较大时，是否会造成multi-bit的问题。 6，接5，是否会造成跳过了full而full+1的状态漏过满。 7，Verilog Coding。 SRAM用于数据的暂时存储，读写地址都由Controller控制，可以随机访问任意地址。FIFO是First in First out的缩写，其读写是有特定顺序的
FIFO深度的计算
luoai_2666的博客
05-16 8408
知乎-硅农 Case9过程有误 即为在160个时钟周期内写入160个数据。 每个时钟读取的数据个数 = 8 / 10 所以160个时钟读出数据的个数为 160 *(8/10） = 128 剩下的没有读出，就存在FIFO中，则需要深度为：160 - 128 = 32 注意：不管读8个数据在10个时钟内是怎么分布的，都不影响结果。但如果条件改成“每100个时钟读取80个数据”，结果就不一样了。 ...
FPGA FIFO深度计算
weixin_30868855的博客
06-19 431
转自：http://comm.chinaaet.com/adi/blogdetail/37555.html 首先，一定要理解清楚FIFO的应用场景，这个会直接关系到FIFO深度的计算，如果是面试官抛出的问题，那么有不清楚的地方，就应该进行询问。如果是笔试或者工程中需要计算FIFO深度的话，那么就需要自己考虑清楚。 其次，异步FIFO，读写时钟不同频，那么FIFO主要用于数据缓存，我们选择...
【FIFO】FIFO 最小深度计算
记录学习历程
05-15 2599
目录 为什么使用 FIFO FIFO 的深度大小 题型及解答 为什么使用 FIFO 当我们需要在两个模块之间进行数据的传输，并且两个模块的时钟是不同的，当一定数量数据传输时为了避免数据出现丢失，而且此时写入数据速率大于读出数据速率时，这时候需要将利用 FIFO 做缓冲。 FIFO 的深度大小 FIFO 的深度（大小）应使 FIFO 可以存储所有较慢的模块不读取的数据。 FIFO 仅在数据以突发形式出现时才起作用；不能有连续的数据进出（比如ADC连续采集数据）。如果有连续的数据流，那么所
FIFO 最小深度计算 举例 总结
helrori
05-24 1081
FIFO 最小深度计算 例子 - 1：f_wr > f_rd，连续读写 写时钟80MHz 读时钟50MHz Burst_Len = 120，也就是要求至少安全写入120个数据 连续写入和连续读取，无空闲时间，写入后立即开始读取 ,读写宽度相同 Sol: 写速率 > 读速率，FIFO迟早会被写满，但它要求至少写入120个数据后FIFO不满。 写入120个数据耗时 120 * 12.5 ns = 1500 ns。 写入开始后FIFO内数据以 30M/Date 速率增加。 数据增加持续了 1500 n
FIFO -- 深度计算
darknessdarkness的博客
03-16 630
FIFO深度的计算公式 参考 https://www.cnblogs.com/dxs959229640/p/8144656.html 求FIFO的最小深度主要有以下要点： 在求解之前需要验证一下在允许的最大时间长度内写入的数据量是否等于读出的数据量，保证有解； 求FIFO深度需要考虑最坏的情形，读写的速率应该相差最大，也就是说需要找出最大的写速率和最小的读速率； 不管什么场景，要确...
FIFO深度计算问题
nuc606的博客
10-20 5742
FIFO深度计算公式： fifo_depth = burst_length - burst_length * X/Y * r_clk/w_clk burst_length ：突发数据个数 X,Y：读时钟周期里，每Y个时钟周期会有X个数据读出FIFO r_clk：读时钟 w_clk：写时钟 1，同步FIFO 对于同步fifo，每100个cycle可以写入80个数据，每10个cycle可以读出8个数据，fifo的深度至少为？ 答： 每100个cycle可以写入80个数据，我们考虑最坏的情况，背靠背模式，空2
计算FIFO最小深度
最新发布
03-30
### 如何计算FIFO缓存的最小深度 在设计FIFO缓存时，其深度的选择至关重要。FIFO深度决定了能够存储的最大数据量以及系统的稳定性和效率。以下是关于如何计算FIFO缓存最小深度的关键点： #### 1. 基本公式推导 对于连续数据流的情况，可以通过以下公式估计FIFO所需的最小深度： \[ \text{FIFO深度} = \frac{\text{写入速率} - \text{读取速率}}{\text{最大容忍延迟时间}} \] 其中，“最大容忍延迟时间”是指系统允许FIFO被完全填满的时间窗口[^1]。 #### 2. 考虑数据包传输特性 当处理分组数据而非连续流时，需考虑单次数据包的大小及其传输时间： \[ \text{FIFO深度} \geq \frac{\text{数据包大小 (bit)}}{\text{写入速率 (bps)} - \text{读取速率 (bps)}} \] 此公式的前提是写入速率高于读取速率。如果写入速率低于读取速率，则需要额外分析应用需求并可能增加FIFO深度以满足特定条件下的稳定性要求[^3]。 #### 3. 实际应用场景中的调整因子 理论计算得出的结果通常是一个理想值，在实际工程实践中还需要加入一定的余量（margin），因为存在如下因素可能导致误差： - **时钟抖动**：即使理论上两路时钟频率相同，也可能因抖动造成短期不匹配； - **突发流量**：某些时刻可能会出现超出平均统计规律的大规模数据涌入现象； - **硬件延时差异**：不同芯片间可能存在制造工艺上的细微偏差影响最终表现。 因此建议按照理论值基础上再乘以一个安全系数K(K>1)，即： \[ \text{实际FIFO深度} = K \times (\text{理论FIFO深度}) \] #### 示例代码展示 下面给出一段简单的Python脚本来帮助快速估算上述提到的各种变量关系: ```python def fifo_depth_calculator(packet_size_bits, write_rate_bps, read_rate_bps, margin_factor=1.2): """Calculate minimum required depth of a FIFO buffer.""" if write_rate_bps <= read_rate_bps: raise ValueError("Write rate must be greater than Read rate to avoid data loss.") theoretical_depth = packet_size_bits / (write_rate_bps - read_rate_bps) actual_depth = int(theoretical_depth * margin_factor) return actual_depth if __name__ == "__main__": PACKET_SIZE_BITS = 8000 # Example value in bits WRITE_RATE_BPS = 1e6 # Write speed in bps READ_RATE_BPS = 900e3 # Read speed in bps result = fifo_depth_calculator(PACKET_SIZE_BITS, WRITE_RATE_BPS, READ_RATE_BPS) print(f"Minimum FIFO Depth Required: {result}") ```
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值