深入解析强化学习之Q-Learning全攻略：理论基础、算法流程与应用实战

最新推荐文章于 2025-03-12 16:36:29 发布

小马不会过河

最新推荐文章于 2025-03-12 16:36:29 发布

阅读量1.5k

点赞数 23

文章标签：算法人工智能百度机器人 embedding

本文链接：https://blog.csdn.net/m0_59163425/article/details/144857221

版权

1. Q-Learning理论基础

1.1 强化学习基本概念

强化学习（Reinforcement Learning, RL）是一种机器学习方法，它通过与环境的交互来学习如何实现特定的目标。在强化学习中，一个智能体（Agent）在环境中通过执行动作（Action）来改变状态（State），并根据状态转移获得奖励（Reward）。智能体的目标是最大化其长期累积奖励，这通常涉及到策略（Policy）的学习，即在给定状态下选择最佳动作的规则。

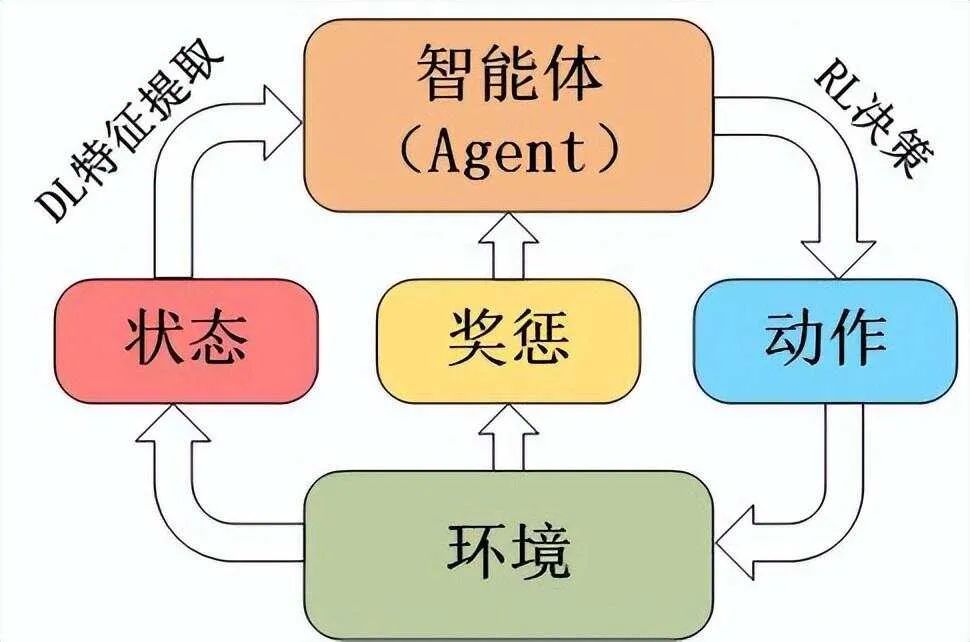
强化学习的关键组成部分包括：

状态（State）：智能体所处的环境情况。
动作（Action）：智能体在特定状态下可以执行的行为。
奖励（Reward）：智能体执行动作后从环境中获得的反馈，用于评价动作的好坏。
策略（Policy）：智能体选择动作的规则或策略，可以是确定性的或随机性的。
价值函数（Value Function）：预测智能体从某个状态出发，遵循特定策略所能获得的累积奖励。

1.2 Q值函数定义

Q值函数，也称为动作价值函数（Action-Value Function），是一种特殊的价值函数，它估计了在给定状态下采取特定动作的预期回报。

Q-Learning算法通过迭代更新Q值来逼近最优Q函数。算法流程包括初始化Q表、选择动作、执行动作、更新Q值等步骤。

1.3 Q-Learning算法流程

初始化Q表：创建一个Q表，通常初始化为零或其他小的随机值。
选择动作：在每个时间步骤中，智能体根据当前状态和Q表选择一个动作。这通常涉及到探索和利用的权衡，以确保在学习过程中不断探索新的动作策略。
执行动作：智能体执行所选择的动作，并观察环境的响应，包括获得的奖励信号和新的状态。
更新Q值：根据观察到的奖励信号和新的状态，智能体更新Q值。这涉及到使用Q-Learning的更新规则，如贝尔曼方程。
重复迭代：智能体不断地执行上述步骤，与环境互动，学习和改进Q值函数，直到达到停止条件。

1.4 Q-Learning计算公式

Q-Learning的核心是更新Q值的公式，该公式基于贝尔曼方程：

其中：

是在状态下采取动作的Q值。
是学习率，控制新估计值与旧估计值之间的权衡。
是在执行动作后获得的即时奖励。
是折扣因子，表示未来奖励的重要性。
是执行动作后观察到的新状态。
是在新状态下选择的下一个动作。

2. Q-Learning算法流程详解

2.1 初始化Q值

Q-Learning算法的第一步是初始化Q值。Q值，或称为动作价值，表示在特定状态下采取特定动作的预期回报。在算法开始时，Q值通常被初始化为零或小的随机数，以表示我们对环境的无知。这个Q表将随着智能体与环境的交互而不断更新和改进。

Q表初始化：Q表是一个二维数组，其中行表示状态，列表示动作。每个单元格表示在状态下采取动作的预期回报。初始化时，对于所有和。

2.2 选择动作与执行

在每个时间步骤中，智能体需要根据当前状态选择一个动作。Q-Learning使用ε-greedy策略来平衡探索（exploration）和利用（exploitation）。

ε-greedy策略：以的概率选择当前Q值最高的动作，以ε的概率随机选择一个动作。这种策略允许智能体在大多数时间利用已知的最佳动作，同时保留一定概率去探索新的动作，以发现可能更好的策略。
动作执行：智能体执行选择的动作，并观察环境的响应，包括获得的奖励信号和新的状态。

2.3 环境反馈与Q值更新

智能体根据环境的反馈更新Q值，这是Q-Learning算法的核心步骤。

奖励和新状态：智能体执行动作后，会收到一个奖励和一个新的状态。
Q值更新：使用以下公式更新Q值：其中：
是学习率，控制新信息的影响程度。
是折扣因子，控制未来奖励的当前价值。
是在新状态下所有可能动作的最大Q值，表示对未来奖励的最大预期。
迭代过程：智能体重复选择动作、执行动作和更新Q值的过程，直到达到某个终止条件，如达到最大迭代次数或Q值收敛。

通过这些步骤，Q-Learning算法能够学习在给定状态下采取哪些动作能够最大化长期累积奖励，而无需了解环境的具体动态。这种无模型的方法使得Q-Learning在许多实际应用中非常有用，尤其是在模型难以获得或过于复杂时。

3. Q-Learning计算公式

3.1 Q值更新公式

Q-Learning的核心计算公式是Q值更新公式，该公式基于贝尔曼方程，并用于迭代地更新状态-动作对的价值估计。Q值更新公式如下：

其中：

是在时间步的状态下采取动作的Q值。
是学习率，它决定了新信息对Q值更新的影响程度。
是在采取动作后获得的即时奖励。
是折扣因子，它反映了未来奖励相对于即时奖励的重要性。
是在新状态下所有可能动作的最大Q值，代表了对未来奖励的最大预期。

这个公式结合了即时奖励和对未来奖励的预期，通过不断更新Q值，智能体可以学习到在每个状态下应该采取哪个动作以最大化长期累积奖励。

3.2 贝尔曼方程与最优策略

贝尔曼方程是动态规划中的核心原理，它描述了一个状态的价值可以通过即时奖励和未来价值的总和来计算。对于Q-Learning来说，贝尔曼方程用于计算最优策略下的Q值，即：

其中：

是在最优策略下状态采取动作 ( a ) 的最优Q值。
是在状态下采取动作获得的即时奖励。
是折扣因子。
是从状态采取动作转移到状态的概率。
是在最优策略下状态的最优价值。

Q-Learning的目标是找到使Q值最大化的策略，即：

这意味着在给定状态下，最优策略是选择能够使Q值最大的动作。通过不断迭代更新Q值，Q-Learning算法能够收敛到最优Q值，从而学习到最优策略。

4. Q-Learning算法特点

4.1 收敛性分析

Q-Learning算法的收敛性是其理论基础的重要组成部分。在一定条件下，Q-Learning能够收敛到最优策略。这些条件包括：

有限状态和动作空间：Q-Learning要求状态空间和动作空间必须是有限集，这样才能保证Q表能够被完全更新。
探索策略：智能体必须对所有状态-动作对进行无限次的探索，以确保Q值能够被准确估计。
学习率衰减：学习率需要随时间衰减，以保证Q值更新的稳定性。
**折扣因子**：折扣因子必须满足，以平衡即时奖励和未来奖励的重要性。

在实际应用中，Q-Learning的收敛性可以通过以下方式进行分析：

迭代次数：随着迭代次数的增加，Q值会逐渐稳定，算法趋于收敛。
奖励信号：奖励信号的一致性和可靠性对Q值的收敛性有重要影响。
探索策略：ε-greedy策略中的ε值对收敛速度和稳定性有显著影响。

4.2 探索与利用平衡

Q-Learning中的探索与利用平衡是通过ε-greedy策略实现的。这种策略允许智能体在探索新动作和利用已知最佳动作之间进行权衡：

探索：以ε的概率随机选择动作，以发现新的状态-动作对和潜在的更高回报。
利用：以的概率选择当前Q表中Q值最高的动作，以利用已有的知识。

ε值的动态调整对平衡探索与利用至关重要：

初始值：初始时，ε值通常设置较高，以促进探索。
衰减：随着学习的进行，ε值逐渐减小，使智能体更多地利用已知的最佳策略。
自适应调整：在某些变体中，ε值可以根据学习进度自适应调整，以优化探索与利用的平衡。

4.3 应用领域

Q-Learning算法因其简单性和有效性，在多个领域得到了广泛应用：

游戏：Q-Learning被广泛应用于各种棋盘游戏和视频游戏的AI开发，如Atari游戏和围棋等。
机器人导航：在机器人技术中，Q-Learning用于训练机器人在复杂环境中进行路径规划和导航。
自动驾驶：自动驾驶系统中，Q-Learning可以帮助车辆学习如何在不同的交通状况下做出决策。
资源管理：在网络和能源领域，Q-Learning用于优化资源分配，如网络流量控制和电力分配。
推荐系统：Q-Learning可以帮助系统学习用户的行为模式，提供个性化的推荐。
自然语言处理：Q-Learning也被用于自然语言处理任务，如对话系统和机器翻译。
健康医疗：在医疗领域，Q-Learning可以用于辅助诊断、治疗计划的制定，以及医疗资源的优化配置。
教育技术：Q-Learning可以用于开发智能教学系统，通过学习学生的行为和反馈来个性化教学内容和方法。

4. 相关案例代码

4.1 迷宫问题求解

在迷宫问题中，Q-Learning算法被用来训练一个智能体找到从起点到终点的最短路径。以下是一个简化的迷宫问题求解案例代码：

import numpy as np      # 迷宫环境设置   maze = np.array([       [0, 0, -1, 0],       [0, -1, -1, 0],       [0, 0, 0, 1]   ])   rows, cols = maze.shape   start, end = (0, 0), (2, 3)      # Q-Learning参数   alpha = 0.1# 学习率   gamma = 0.9# 折扣因子   epsilon = 0.1# 探索概率      # 初始化Q表   Q = np.zeros((rows, cols, 4))  # 4个动作：上、下、左、右      # 动作索引   actions = {       0: (-1, 0),  # 上       1: (1, 0),   # 下       2: (0, -1),  # 左       3: (0, 1)    # 右   }      # 训练过程   for episode in range(1000):       state = start       while state != end:           if np.random.rand() < epsilon:               action_index = np.random.choice([0, 1, 2, 3])           else:               action_index = np.argmax(Q[state[0], state[1]])                      action = actions[action_index]           next_state = (state[0] + action[0], state[1] + action[1])                      # 检查边界和障碍           if0 <= next_state[0] < rows and0 <= next_state[1] < cols and maze[next_state[0], next_state[1]] != -1:               reward = 0               if next_state == end:                   reward = 1               # 更新Q表               Q[state[0], state[1], action_index] += alpha * (reward + gamma * np.max(Q[next_state[0], next_state[1]]) - Q[state[0], state[1], action_index])               state = next_state           else:               # 撞墙，惩罚               Q[state[0], state[1], action_index] += alpha * (-1 - Q[state[0], state[1], action_index])      # 输出最终的Q表   print("Final Q-Table:")   print(Q)

4.2 游戏表格路径寻找

Q-Learning算法也可以应用于基于表格的游戏中，以寻找最优路径。以下是一个简化的游戏表格路径寻找案例代码：

import numpy as np      # 游戏环境设置   game_board = np.array([       [1, 0, 0, 0],       [0, -1, 0, 0],       [0, 0, 0, 1],       [0, 0, -1, 1]   ])   start, end = (0, 0), (3, 3)      # Q-Learning参数   alpha = 0.1# 学习率   gamma = 0.9# 折扣因子   epsilon = 0.1# 探索概率      # 初始化Q表   Q = np.zeros((4, 4, 4))  # 4x4游戏板，4个动作      # 动作索引   actions = {       0: (-1, 0),  # 上       1: (1, 0),   # 下       2: (0, -1),  # 左       3: (0, 1)    # 右   }      # 训练过程   for episode in range(1000):       state = start       while state != end:           if np.random.rand() < epsilon:               action_index = np.random.choice([0, 1, 2, 3])           else:               action_index = np.argmax(Q[state[0], state[1]])                      action = actions[action_index]           next_state = (state[0] + action[0], state[1] + action[1])                      # 检查边界           if0 <= next_state[0] < 4and0 <= next_state[1] < 4:               reward = game_board[next_state[0], next_state[1]]               # 更新Q表               Q[state[0], state[1], action_index] += alpha * (reward + gamma * np.max(Q[next_state[0], next_state[1]]) - Q[state[0], state[1], action_index])               state = next_state           else:               # 边界外，惩罚               Q[state[0], state[1], action_index] += alpha * (-1 - Q[state[0], state[1], action_index])      # 输出最终的Q表   print("Final Q-Table:")   print(Q)

以上代码展示了如何使用Q-Learning算法解决迷宫问题和游戏表格路径寻找问题。通过不断的迭代和学习，智能体能够学习到在不同状态下采取不同动作的最优策略。

如何学习大模型 AI ？

由于新岗位的生产效率，要优于被取代岗位的生产效率，所以实际上整个社会的生产效率是提升的。

但是具体到个人，只能说是：

“最先掌握AI的人，将会比较晚掌握AI的人有竞争优势”。

这句话，放在计算机、互联网、移动互联网的开局时期，都是一样的道理。

我在一线互联网企业工作十余年里，指导过不少同行后辈。帮助很多人得到了学习和成长。

我意识到有很多经验和知识值得分享给大家，也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

在这里插入图片描述