本文围绕CNN卷积层展开，介绍了前向传播和反向传播的相关内容。前向传播采用im2col方法将输入数据转化为二维矩阵方便计算，并给出基本变量及结果大小公式；反向传播求db、dW、dx，用到col2im方法，还给出了相关计算过程，最后提及Convolution层的代码。
参考：
鱼书《深度学习入门》——斋藤康毅
【精选】im2col函数实现超级详细解释_sty945的博客-CSDN博客
介绍高维数组：https://zhuanlan.zhihu.com/p/650178588，博主从索引的角度出发，有利于理解和应用
前向传播
基本变量：
S
S
S: stride，步长
p
a
d
pad
pad: 填充数，表示在图像一侧添加的0的行数或列数
F
H
,
F
W
,
F
N
FH, FW, FN
FH,FW,FN: 滤波器（权重）的宽度、高度和数量
H
,
W
,
N
,
C
H, W, N, C
H,W,N,C: 图像宽、高、数量（batch_size）、通道数
O
H
,
O
W
OH, OW
OH,OW: 滤波器（权重）在图像上滑动，实现
x
⋅
w
x \cdot w
x⋅w操作后生成的结果大小，公式如下：
O
H
=
1
+
H
+
2
⋅
p
a
d
−
F
H
S
O
W
=
1
+
W
+
2
⋅
p
a
d
−
F
H
S
OH = 1 + \frac{H+ 2 \cdot pad -FH}{S}\\ OW = 1 + \frac{W+ 2 \cdot pad -FH}{S}
OH=1+SH+2⋅pad−FHOW=1+SW+2⋅pad−FH
input_data: 以下用x表示，也就是输入数据or图像，形状为N, Cm H, W
W: 也就是滤波器or权重，形状为FN, C, FH, FW
将x转化为更高维的矩阵，方便计算，采用im2col方法：
im2col方法
原理：
参考：【精选】im2col函数实现超级详细解释_sty945的博客-CSDN博客 博主讲的非常好，建议看一下。
目的是生成常见的二维矩阵col方便计算和理解。
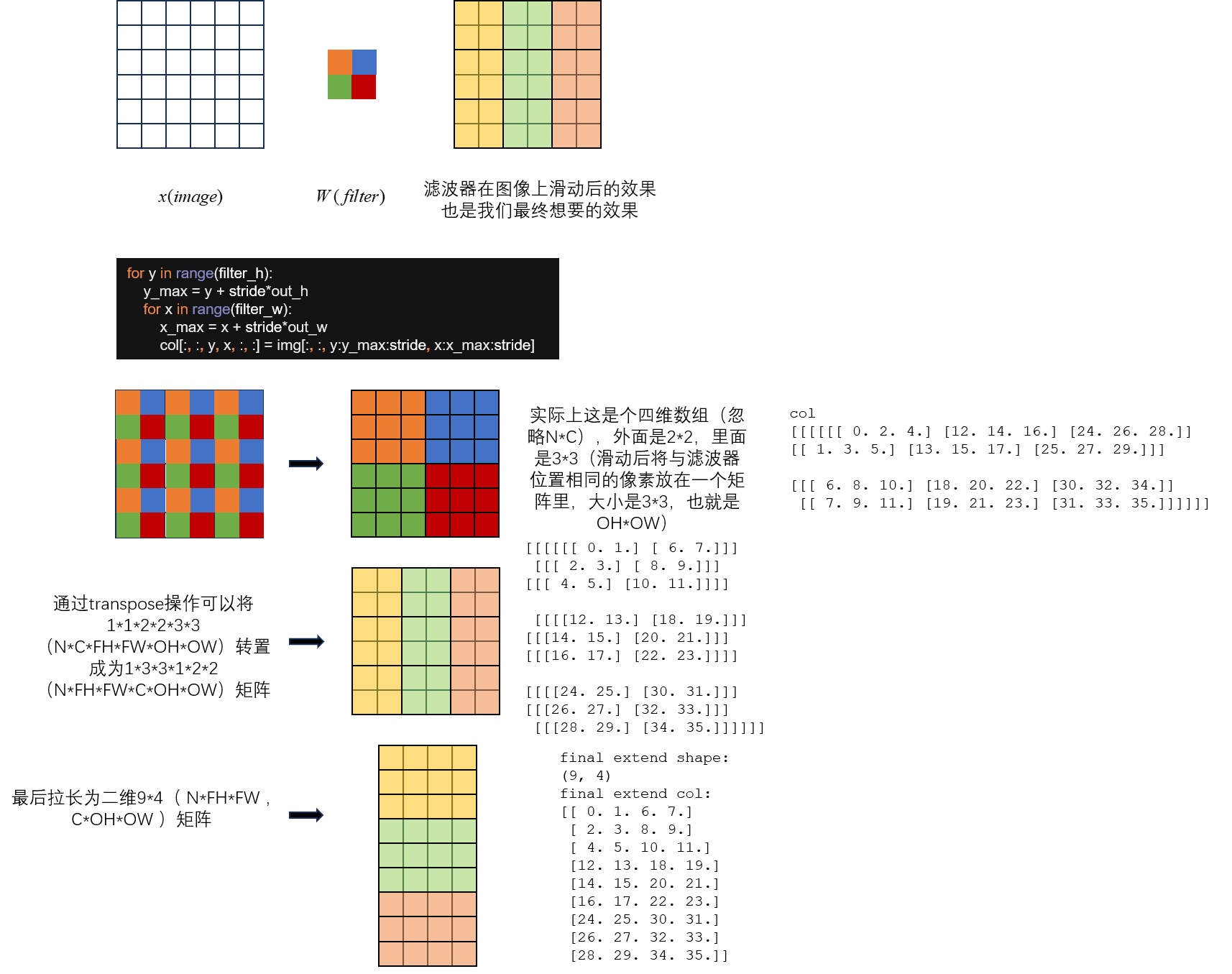
比如，一个1 * 1 * 6 * 6的单通道输入，滤波器为1 * 1 * 2 * 2，步长为2，填充为0，我们通过观看输入来思考这个方法的实现。
滤波器在图像上滑动，得到一个个包含像素点的小块，滑动的结果放在OH, OW大小的矩阵里，看图示：
import numpy as np
filter_h = 2
filter_w = 2
stride = 2
pad = 0
shape_size = 6
C = 1
N = 1
mul = C * N * shape_size ** 2
input_data = np.arange(mul)
input_data = input_data.reshape(N, C, shape_size, shape_size)
print('original img:\n', input_data)
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
print('input data with pad:\n', img)
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
print('shape of structing col:\n', col.shape)
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
print('\ny:', y, 'x:', x, 'y_max', y_max, 'x_max', x_max)
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
print('\ncol\n', col)
print('---------------------')
# 不用关心y_max和x_max会越界，他们不重要
print('original shape after for loop:\n', col.shape, '\n original after for loop:\n', col)
print("====================================")
print('col transpose shape: \n', col.transpose(0, 4, 5, 1, 2, 3).shape,
'\ncol transopose data: \n', col.transpose(0, 4, 5, 1, 2, 3))
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
col = im2col(input_data, filter_h, filter_w, stride, pad)
print('final extend shape:\n ', col.shape, '\nfinal extend col:\n' ,col)
输出：
original img:
[[[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]
[24 25 26 27 28 29]
[30 31 32 33 34 35]]]]
input data with pad:
[[[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]
[24 25 26 27 28 29]
[30 31 32 33 34 35]]]]
shape of structing col:
(1, 1, 2, 2, 3, 3)
y: 0 x: 0 y_max 6 x_max 6
col
[[[[[[ 0. 2. 4.]
[12. 14. 16.]
[24. 26. 28.]]
[[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]]
[[[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
[[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]]]]]
---------------------
y: 0 x: 1 y_max 6 x_max 7
col
[[[[[[ 0. 2. 4.]
[12. 14. 16.]
[24. 26. 28.]]
[[ 1. 3. 5.]
[13. 15. 17.]
[25. 27. 29.]]]
[[[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
[[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]]]]]
---------------------
y: 1 x: 0 y_max 7 x_max 6
col
[[[[[[ 0. 2. 4.]
[12. 14. 16.]
[24. 26. 28.]]
[[ 1. 3. 5.]
[13. 15. 17.]
[25. 27. 29.]]]
[[[ 6. 8. 10.]
[18. 20. 22.]
[30. 32. 34.]]
[[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]]]]]
---------------------
y: 1 x: 1 y_max 7 x_max 7
col
[[[[[[ 0. 2. 4.]
[12. 14. 16.]
[24. 26. 28.]]
[[ 1. 3. 5.]
[13. 15. 17.]
[25. 27. 29.]]]
[[[ 6. 8. 10.]
[18. 20. 22.]
[30. 32. 34.]]
[[ 7. 9. 11.]
[19. 21. 23.]
[31. 33. 35.]]]]]]
---------------------
original shape after for loop:
(1, 1, 2, 2, 3, 3)
original after for loop:
[[[[[[ 0. 2. 4.]
[12. 14. 16.]
[24. 26. 28.]]
[[ 1. 3. 5.]
[13. 15. 17.]
[25. 27. 29.]]]
[[[ 6. 8. 10.]
[18. 20. 22.]
[30. 32. 34.]]
[[ 7. 9. 11.]
[19. 21. 23.]
[31. 33. 35.]]]]]]
====================================
col transpose shape:
(1, 3, 3, 1, 2, 2)
col transopose data:
[[[[[[ 0. 1.]
[ 6. 7.]]]
[[[ 2. 3.]
[ 8. 9.]]]
[[[ 4. 5.]
[10. 11.]]]]
[[[[12. 13.]
[18. 19.]]]
[[[14. 15.]
[20. 21.]]]
[[[16. 17.]
[22. 23.]]]]
[[[[24. 25.]
[30. 31.]]]
[[[26. 27.]
[32. 33.]]]
[[[28. 29.]
[34. 35.]]]]]]
final extend shape:
(9, 4)
final extend col:
[[ 0. 1. 6. 7.]
[ 2. 3. 8. 9.]
[ 4. 5. 10. 11.]
[12. 13. 18. 19.]
[14. 15. 20. 21.]
[16. 17. 22. 23.]
[24. 25. 30. 31.]
[26. 27. 32. 33.]
[28. 29. 34. 35.]]
前向传播变量的计算
| variable | shape |
|---|---|
| W | FN, C, FH, FW |
| x | N, C, H, W |
| x -> col(调用im2col方法) | N, C, FH, FW, OH, OW -> N*OH*OW, C*FH*FW |
| W -> col_W | C*FH*FW, FN |
| b | FN |
| y = x ⋅ W + b y=x \cdot W + b y=x⋅W+b | N*OH*OW, FN |
| y | N, FN, OH, OW |
反向传播
也就是求db，dW，dx，基本原理与Affine一致，但是需要用到col2im方法。
col2im原理
整个过程都是im2col的逆序，先把col从二维变回六维，然后再转置变回最初形状为N, C, FH, FW, OH, OW。现在img形状是N, C, H, W，但是内容都为0，需要把col的内容填回去。
填回去的代码用的是img[:, :, y:y_max:stride, x:x_max:stride] = col[:, :, y, x, :, :]，鱼书代码是img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]，但是我发现这里有个问题，如果pad=2，stride=1，H和W都为6，其他不变的时候，这个累加过程会让最后结果不断累加（你们可以试试），我不知道这一块是我理解错了还是说作者有问题，请教一下各位大佬。
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
col :
input_shape : 输入数据的形状（例：(10, 1, 28, 28)）
filter_h :
filter_w
stride
pad
Returns
-------
"""
N, C, H, W = input_shape
print(N, C, H, W)
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
print('ere im2col and reshape:\n', col.reshape(N, out_h, out_w, C, filter_h, filter_w))
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
print('ere im2col, reshape and transpose :\n', col)
img = np.zeros((N, C, H + 2*pad, W + 2*pad))
# 创建img存储数据，而且要包含pad，否则越界
print('img:\n',img)
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
print('y:', y, 'x:', x, 'y_max:', y_max, 'x_max:', x_max)
img[:, :, y:y_max:stride, x:x_max:stride] = col[:, :, y, x, :, :]
print('\n img:', y, x, ':\n', img)
print('image shape:', img.shape)
return img[:, :, pad:H + pad, pad:W + pad]
# print('image shape:', img.shape)
input_shape = input_data.shape
print('original img', img)
print('original col', col)
img = col2im(col, input_shape, filter_h, filter_w, stride, pad)
print('final img', img)
输出：
original img [[[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. 9. 10. 11.]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. 22. 23.]
[24. 25. 26. 27. 28. 29.]
[30. 31. 32. 33. 34. 35.]]]]
original col [[ 0. 1. 6. 7.]
[ 2. 3. 8. 9.]
[ 4. 5. 10. 11.]
[12. 13. 18. 19.]
[14. 15. 20. 21.]
[16. 17. 22. 23.]
[24. 25. 30. 31.]
[26. 27. 32. 33.]
[28. 29. 34. 35.]]
1 1 6 6
after im2col and reshape:
[[[[[[ 0. 1.]
[ 6. 7.]]]
[[[ 2. 3.]
[ 8. 9.]]]
[[[ 4. 5.]
[10. 11.]]]]
[[[[12. 13.]
[18. 19.]]]
[[[14. 15.]
[20. 21.]]]
[[[16. 17.]
[22. 23.]]]]
[[[[24. 25.]
[30. 31.]]]
[[[26. 27.]
[32. 33.]]]
[[[28. 29.]
[34. 35.]]]]]]
after im2col, reshape and transpose :
[[[[[[ 0. 2. 4.]
[12. 14. 16.]
[24. 26. 28.]]
[[ 1. 3. 5.]
[13. 15. 17.]
[25. 27. 29.]]]
[[[ 6. 8. 10.]
[18. 20. 22.]
[30. 32. 34.]]
[[ 7. 9. 11.]
[19. 21. 23.]
[31. 33. 35.]]]]]]
img:
[[[[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]]]
y: 0 x: 0 y_max: 6 x_max: 6
img: 0 0 :
[[[[ 0. 0. 2. 0. 4. 0.]
[ 0. 0. 0. 0. 0. 0.]
[12. 0. 14. 0. 16. 0.]
[ 0. 0. 0. 0. 0. 0.]
[24. 0. 26. 0. 28. 0.]
[ 0. 0. 0. 0. 0. 0.]]]]
y: 0 x: 1 y_max: 6 x_max: 7
img: 0 1 :
[[[[ 0. 1. 2. 3. 4. 5.]
[ 0. 0. 0. 0. 0. 0.]
[12. 13. 14. 15. 16. 17.]
[ 0. 0. 0. 0. 0. 0.]
[24. 25. 26. 27. 28. 29.]
[ 0. 0. 0. 0. 0. 0.]]]]
y: 1 x: 0 y_max: 7 x_max: 6
img: 1 0 :
[[[[ 0. 1. 2. 3. 4. 5.]
[ 6. 0. 8. 0. 10. 0.]
[12. 13. 14. 15. 16. 17.]
[18. 0. 20. 0. 22. 0.]
[24. 25. 26. 27. 28. 29.]
[30. 0. 32. 0. 34. 0.]]]]
y: 1 x: 1 y_max: 7 x_max: 7
img: 1 1 :
[[[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. 9. 10. 11.]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. 22. 23.]
[24. 25. 26. 27. 28. 29.]
[30. 31. 32. 33. 34. 35.]]]]
image shape: (1, 1, 6, 6)
final img [[[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. 9. 10. 11.]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. 22. 23.]
[24. 25. 26. 27. 28. 29.]
[30. 31. 32. 33. 34. 35.]]]]
反向传播计算
我们复习一下Affine：
∂
L
∂
x
=
∂
L
∂
Y
(
d
o
u
t
)
⋅
W
T
∂
L
∂
W
=
X
T
⋅
∂
L
∂
Y
(
d
o
u
t
)
\frac {\partial L}{\partial x} = \frac{\partial L}{\partial Y}(dout) \cdot W^\text{T}\\ \frac {\partial L}{\partial W} = X^\text{T} \cdot \frac{\partial L}{\partial Y} (dout)
∂x∂L=∂Y∂L(dout)⋅WT∂W∂L=XT⋅∂Y∂L(dout)
需要计算db，dW，dx。db不多说，主要是dW和dx。
| variable | shape |
|---|---|
| dout | N*OH*OW, FN |
| W(即col_W) | C*FH*FW, FN |
| X(即col) | N*OH*OW, C*FH*FW |
dW在计算col的转置与dout的矩阵乘法后，还需要变成原来四维的形状，也就是FN, C, FH, FW
计算dx时首先计算dcol，这是因为我们要的x的梯度应该是img形状的，但是需要先从二维入手，变为四维。也就是说，self.dW = np.dot(self.col.T, dout)即
d
W
=
c
o
l
T
×
d
o
u
t
dW = col^\text{T} \times dout
dW=colT×dout，然后用col2img方法变为img形状。
Convolution层的代码
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 中间数据（backward时使用）
self.x = None
self.col = None
self.col_W = None
# 权重和偏置参数的梯度
self.dW = None
self.db = None
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0,2,3,1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
扫一扫
635
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
