【目标定位】基于卡尔曼滤波实现UWB-IMU组合定位导航matlab代码

1 简介

基于 UWB 无线电技术的小区域导航技术已被愈发广泛的应用于实际场景中，然而 NLOS 误差严重会影响到系统的速度与位置的估计精度。为了提高 UWB 导航系统的鲁棒性，利用 EKF 滤波器实现 UWB /IMU 的紧组合，对载体的速度进行估计，并基于残差卡方检测原理判别是否出现 NLOS，通过减小异常测量值的权重来减弱 NLOS 对载体速度估计的影响。而后设计 α － β 滤波器，融合载体的速度信息，对由牛顿迭代法求解的位置估计结果进行平滑处理。仿真结果表明，设计的算法能够有效抑制 NLOS 干扰对载体速度估计的影响，有助于进一步实现无人设备在小区域内的内外环控制任务。

2 部分代码

clc
clear all
close all
global UKF;

addpath('ekfukf');
load('ground_truth.mat')
% Measurement model and it's derivative
f_func = @ekf_ins_f;
df_dx_func = @ekf_err_ins_f;
h_func = @ekf_uwb_h;
dh_dx_func = @ekf_err_uwb_h;

% anchor position 
UKF.BSOneCoordinate = [9.21;1.08;-0.17];%4.08
UKF.BSTwoCoordinate = [0;0;-1.885];
UKF.BSThreeCoordinate = [0;6.281;-1.37];
UKF.BSFourCoordinate = [1.705;12.88;-2.27];
UKF.BSFiveCoordinate = [9.31;11.59;-0.52];
UKF.BaseS_Position = [UKF.BSOneCoordinate,UKF.BSTwoCoordinate,...
  UKF.BSThreeCoordinate,UKF.BSFourCoordinate,...
  UKF.BSFiveCoordinate]*30;
UKF.bSPcs = 5;

% download the sensor data
matfile = dir('*_HandledFileToMatData.mat');
if isempty(matfile)
   disp('           None Found *_HandledFileToMatData.mat')
end

for ki=1:size(matfile)
   load(matfile(ki).name)
end

% initialization
ProcessNoiseVariance = [3.9e-04    4.5e-4       7.9e-4;   %%%Accelerate_Variance
                       1.9239e-7, 3.5379e-7, 2.4626e-7;%%%Accelerate_Bias_Variance
                       8.7e-04,1.2e-03,1.1e-03;      %%%Gyroscope_Variance
                       1.3111e-9,2.5134e-9,    2.4871e-9    %%%Gyroscope_Bias_Variance
                    ];  
Q = [  diag(ProcessNoiseVariance(1,:)),zeros(3,12); 
zeros(3,3), diag(ProcessNoiseVariance(1,:)),zeros(3,9); 
zeros(3,6), diag(ProcessNoiseVariance(3,:)),zeros(3,6); 
zeros(3,9),  diag(ProcessNoiseVariance(2,:)),zeros(3,3);
zeros(3,12), diag(ProcessNoiseVariance(4,:))];  
MeasureNoiseVariance =[2.98e-03,2.9e-03,...
   1.8e-03,1.2e-03,...
   2.4e-03];%%%%uwb ranging noise
R = diag(MeasureNoiseVariance);

Position_init =[20;100;-1.9];    deta_Position_init = [0;0;0];
Speed_init = [0;0;0];              deta_Speed_init = [0;0;0];   
Accelerate_Bias_init = [0;0;0];    deta_Accelerate_Bias_init = [0;0;0];   
Gyroscope_Bias_init = [0;0;0];     deta_Gyroscope_Bias_init = [0;0;0];   
Quaternion_init = [1,0,0,0]';    deta_Quaternion_init = [0;0;0;0];        

% state init x0 and P0   
X0 = [Position_init;Speed_init;Accelerate_Bias_init;Gyroscope_Bias_init;Quaternion_init];

StaticBiasAccelVariance =[6.7203e-5,      8.7258e-5,       4.2737e-5];
StaticBiasGyroVariance =   [2.2178e-5,     5.9452e-5,        1.3473e-5];

init_c = 0.1;
P0 = [init_c*eye(3,3),zeros(3,12);
     zeros(3,3) ,  1e-2*init_c*eye(3,3),zeros(3,9);
  zeros(3,6),  1e-2*init_c* eye(3,3),zeros(3,6);
     zeros(3,9),   diag(StaticBiasGyroVariance),zeros(3,3);
     zeros(3,12),   diag( StaticBiasAccelVariance);
    ];  

% Initial guesses for the state mean and covariance.
X = [2;2;-3;zeros(3,1);10/180*pi;-10/180*pi;20/180*pi;...
    sqrt(StaticBiasAccelVariance').*randn(3,1);
sqrt(StaticBiasGyroVariance').*randn(3,1)
];
dX = [zeros(9,1);   
    sqrt(StaticBiasAccelVariance').*randn(3,1);
sqrt(StaticBiasGyroVariance').*randn(3,1)];

   MM(:,k)   = X;
   PP(:,:,k) = P;
  imu_iter = imu_iter + 1;
end  

MM(7:9,:)= MM(7:9,:)/pi*180;
noise = noise';
for uwb_iter=1:4:length(UWBBroadTime_vector)-10
    Z_meas = diag(Uwbranging_vector(uwb_iter:uwb_iter+4,:) +  noise(uwb_iter:uwb_iter+4,:)) ;
       uwbxyz = triangulate(Z_meas);
UWBXYZ = [UWBXYZ,[UWBBroadTime_vector(uwb_iter+2);uwbxyz;TraceData(4*(uwb_iter+2)+1,2:4)']];
end
%-------------- figure 1: display trajectory ----------------------%
base = 1;
figure(1)
subplot(311)
plot(TraceData(:,1),TraceData(:,base+1),'g.')
hold on
plot(SampleTimePoint(1:Pcs),MM(base,:),'m')
plot(UWBXYZ(1,:),UWBXYZ(2,:),'k')
title('Position x Axis');xlabel('T:s');ylabel('X axis:m');grid on;
legend('Real Trajectory','UWB-IMU Trajectory','UWB Trajectory')

subplot(312)
plot(TraceData(:,1),TraceData(:,base+2),'g.')
hold on
plot(SampleTimePoint(1:Pcs),MM(base+1,:),'m')
plot(UWBXYZ(1,:),UWBXYZ(3,:),'k')
title('Position y Axis');xlabel('T:s');ylabel('Y axis:m');grid on;
legend('Real Trajectory','UWB-IMU Trajectory','UWB Trajectory')

subplot(313)
plot(TraceData(:,1),TraceData(:,base+3),'g.')
hold on
plot(SampleTimePoint(1:Pcs),MM(base+2,:),'m')
plot(UWBXYZ(1,:),UWBXYZ(4,:),'k')
title('Position z Axis');xlabel('T:s');ylabel('Z axis:m');grid on;
legend('Real Trajectory','UWB-IMU Trajectory','UWB Trajectory')

%-------------- figure 2: display trajectory error -----------------%
base = 1;
figure(2)
subplot(331)
plot(SampleTimePoint(1:Pcs),MM(base,:)'- TraceData(:,base+1),'m');
hold on
plot(UWBXYZ(1,:),UWBXYZ(2,:) - UWBXYZ(5,:),'k')
title('Position x Axis');xlabel('T:s');ylabel('X axis:m');grid on;
legend('UWB-IMU Trajectory Error','UWB Trajectory Error')

subplot(332)
xvalues1 = -3:0.2:3;
error = MM(base,:)'- TraceData(:,base+1);
hist(error(find(error < 3 & error > -3)),100);
title('Position x Axis Error Hist');grid on;
legend('UWB-IMU Trajectory Error')

h=subplot(333);
error =UWBXYZ(2,:) - UWBXYZ(5,:);
hist(error(find(error < 3 & error > -3)),100);
hp = findobj(h,'Type','patch');
set(hp,'FaceColor',[0 .5 .5],'EdgeColor','w')
title('Position x Axis Error Hist');grid on;
legend('UWB Trajectory Error')

subplot(334)
hold on
plot(SampleTimePoint(1:Pcs),MM(base+1,:)' - TraceData(:,base+2),'m')
plot(UWBXYZ(1,:),UWBXYZ(3,:) - UWBXYZ(6,:),'k')
title('Position y Axis');xlabel('T:s');ylabel('Y axis:m');grid on;
legend('UWB-IMU Trajectory Error','UWB Trajectory Error')

subplot(335)
xvalues1 = -3:0.2:3;
error = MM(base+1,:)'- TraceData(:,base+2);
hist(error(find(error < 3 & error > -3)),100);
title('Position x Axis Error Hist');grid on;
legend('UWB-IMU Trajectory Error')

h=subplot(336);
error =UWBXYZ(3,:) - UWBXYZ(6,:);
hist(error(find(error < 3 & error > -3)),100);
hp = findobj(h,'Type','patch');
set(hp,'FaceColor',[0 .5 .5],'EdgeColor','w')
title('Position x Axis Error Hist');grid on;
legend('UWB Trajectory Error')

subplot(337)
hold on
plot(SampleTimePoint(1:Pcs),MM(base+2,:)' - TraceData(:,base+3),'m')
plot(UWBXYZ(1,:),UWBXYZ(4,:) - UWBXYZ(7,:),'k')
title('Position z Axis');xlabel('T:s');ylabel('Z axis:m');grid on;
legend('UWB-IMU Trajectory Error','UWB Trajectory Error')

subplot(338)
xvalues1 = -10:0.2:10;
error = MM(base+2,:)'- TraceData(:,base+3);
hist(error(find(error < 10 & error > -10)),100);
title('Position x Axis Error Hist');grid on;
legend('UWB-IMU Trajectory Error')

h=subplot(339);
error =UWBXYZ(4,:) - UWBXYZ(7,:);
hist(error(find(error < 10 & error > -10)),100);
hp = findobj(h,'Type','patch');
set(hp,'FaceColor',[0 .5 .5],'EdgeColor','w')
title('Position x Axis Error Hist');grid on;
legend('UWB Trajectory Error')

%-------------- figure 3: display Speed state -----------------%
base = 4;
figure(3)
subplot(311)
plot(TraceData(:,1),TraceData(:,base+1),'r*');grid on
hold on
plot(SampleTimePoint(1:Pcs),MM(base,:),'k')
title('Speed x Axis');xlabel('T:s');ylabel('x axis:m');grid on;

subplot(312)
plot(TraceData(:,1),TraceData(:,base+2),'g*');grid on
hold on
plot(SampleTimePoint(1:Pcs),MM(base+1,:),'k')
title('Speed y Axis');xlabel('T:s');ylabel('y axis:m');grid on;

subplot(313)
plot(TraceData(:,1),TraceData(:,base+3),'c*');grid on
hold on
plot(SampleTimePoint(1:Pcs),MM(base+2,:),'k')
title('Speed z Axis');xlabel('T:s');ylabel('z axis:m');grid on;


%-------------- figure 4: display Pose state -----------------%
base = 7;
figure(4)
subplot(311)
plot(TraceData(:,1),TraceData(:,base+1),'r*')
hold on;grid on;
plot(SampleTimePoint(1:Pcs),MM(base,:),'k')
title('Euler');grid on;
legend('Real Atti','UWB-IMU Atti')

subplot(312)
plot(TraceData(:,1),TraceData(:,base+2),'g*')
hold on
plot(SampleTimePoint(1:Pcs),MM(base+1,:),'k')
title('Euler');grid on;
legend('Real Atti','UWB-IMU Atti')

subplot(313)
plot(TraceData(:,1),TraceData(:,base+3),'c*')
hold on
plot(SampleTimePoint(1:Pcs),MM(base+2,:),'k')
title('Euler');grid on;
legend('Real Atti','UWB-IMU Atti')

%-------------- figure 5: display estimated accel bias ----------%
base = 10;
figure(5)
subplot(311)
plot(TraceData(:,1),TraceData(:,base+1),'r*')
hold on
plot(SampleTimePoint(1:Pcs),MM(base,:),'k')
title('Accel Bias');grid on;
legend('Real Error','UWB-IMU Error')

subplot(312)
plot(TraceData(:,1),TraceData(:,base+2),'g*')
hold on
plot(SampleTimePoint(1:Pcs),MM(base+1,:),'k')
title('Accel Bias');grid on;
legend('Real Error','UWB-IMU Error')

subplot(313)
plot(TraceData(:,1),TraceData(:,base+3),'c*')
hold on
plot(SampleTimePoint(1:Pcs),MM(base+2,:),'k')
title('Accel Bias');grid on;
legend('Real Error','UWB-IMU Error')

%-------------- figure 6: display estimated gyro bias ----------%
base = 13;
figure(6)
subplot(311)
plot(TraceData(:,1),TraceData(:,base+1),'r*')
hold on
plot(SampleTimePoint(1:Pcs),MM(base,:),'k')
title('Gyro Bias');grid on;
legend('Real Error','UWB-IMU Error')

subplot(312)
plot(TraceData(:,1),TraceData(:,base+2),'g*')
hold on
plot(SampleTimePoint(1:Pcs),MM(base+1,:),'k')
title('Gyro Bias');grid on;
legend('Real Error','UWB-IMU Error')

subplot(313)
plot(TraceData(:,1),TraceData(:,base+3),'c*')
hold on
plot(SampleTimePoint(1:Pcs),MM(base+2,:),'k')
title('Gyro Bias');grid on;
legend('Real Error','UWB-IMU Error')

3 仿真结果

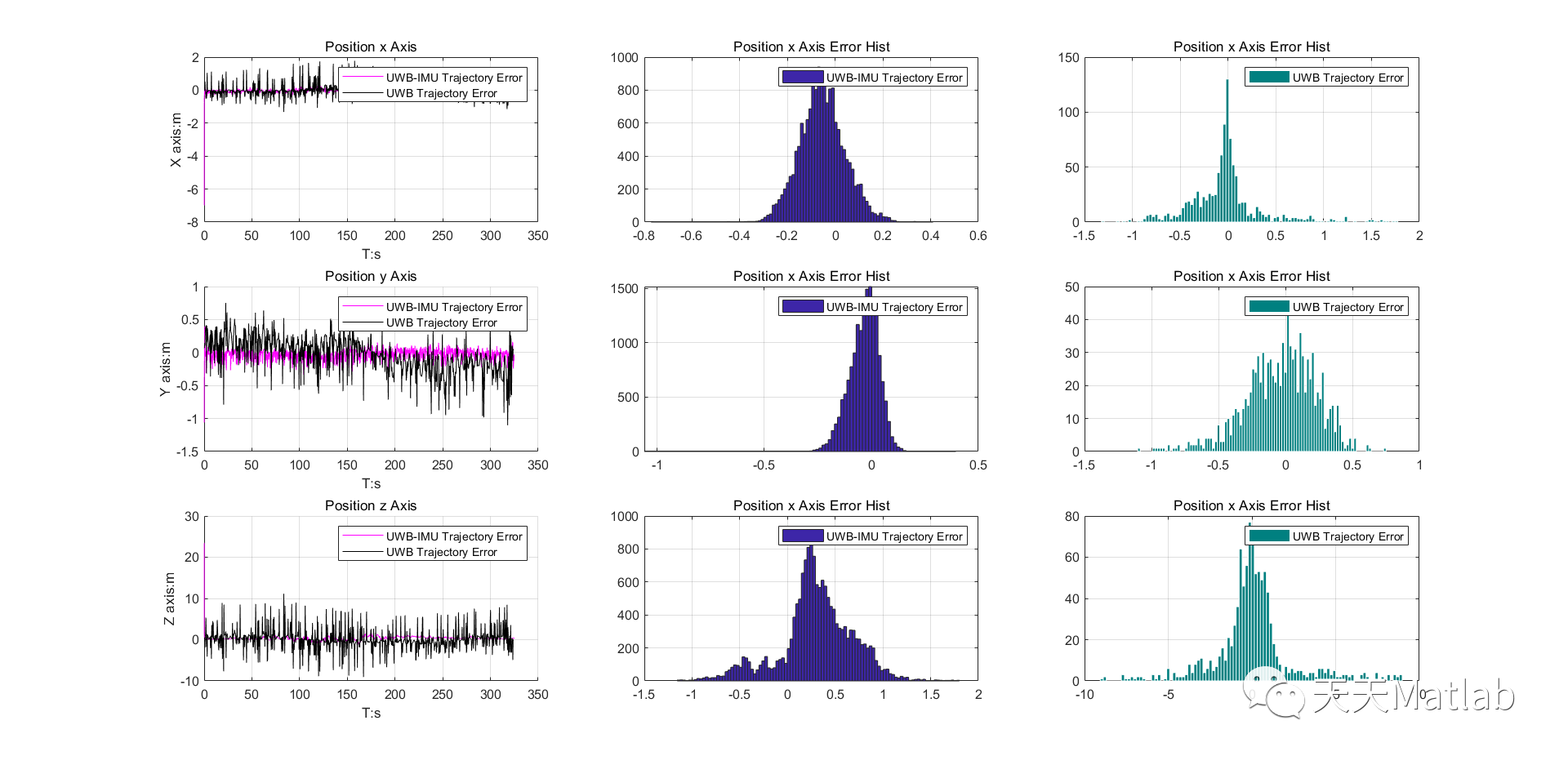
4 参考文献