CINTA 第四次作业

第六章

7.设$\mathbb{G}$是群，对任意$n\in \mathbb{N}$, $i\in [0,n]$，$g_i\in \mathbb{G}$。证明$g_0{g}_1\cdots g_n$的逆元是$g_n^{-1}\cdots g_1^{-1}{g}_0^{-1}$。

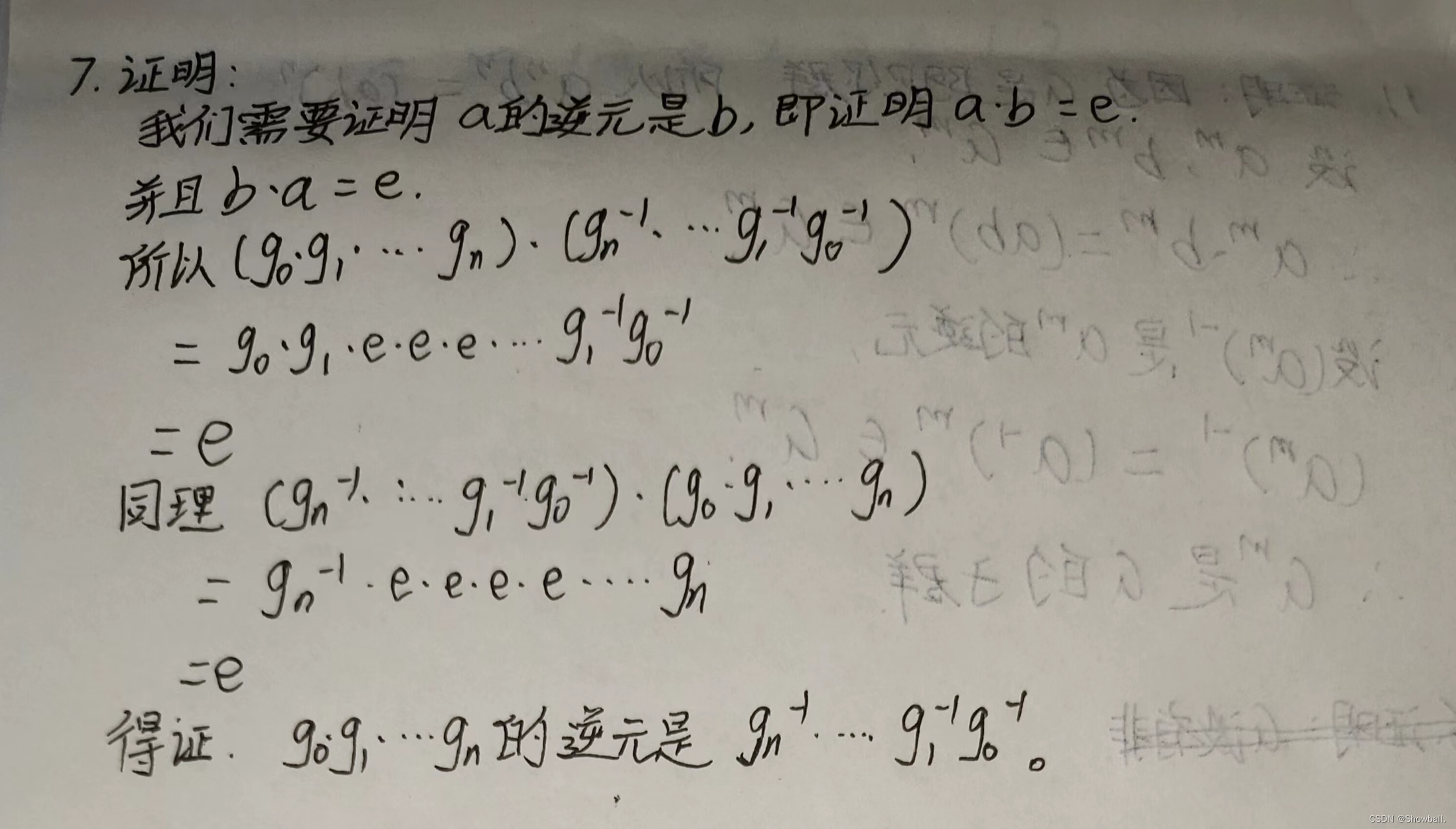
8.证明：任意群$\mathbb{G}$的两个子群的交集也是群$\mathbb{G}$的子群。

10. $\mathbb{G}$是阿贝尔群，$\mathbb{H}$和 $\mathbb{K}$是$\mathbb{G}$的子群。请证明 H K = { h k : h ∈ H , k ∈ K } \mathbb{H} \mathbb{K} = \{hk: h \in \mathbb{H}, k \in \mathbb{K}\} HK={hk:h∈H,k∈K}是群$\mathbb{G}$的子群。
如果$\mathbb{G}$不是阿贝尔群，结论是否依然成立？

11. 设$\mathbb{G}$是阿贝尔群，$m$是任意整数，记 G m = { g m : g ∈ G } \mathbb{G}^m = \{ g^m: g\in \mathbb{G}\} Gm={gm:g∈G}。请证明${\mathbb{G}}^m$是$\mathbb{G}$的一个子群。

第七章

6.证明：如果群$\mathbb{G}$没有非平凡子群，则群$\mathbb{G}$是循环群。
证明：$\mathbb{G}$没有非平凡子群，所以$\mathbb{G}$只有{e}和$\mathbb{G}$两个子群，那么很显然，群$\mathbb{G}$中任意一个非单位元素都可以生成$\mathbb{G}$，因此$\mathbb{G}$为循环群。综上，得证。

7.证明循环群$\mathbb{G}$中任意元素的阶都整除群$\mathbb{G}$的阶。

8.编程完成以下工作：给定一个素数$p$，找出${\mathbb{Z}}_p^{\ast }$的最小生成元。对于素数$1<p<10000$，哪一个素数$p$使得${\mathbb{Z}}_p^{\ast }$的最小生成元最大？

#include<bits/stdc++.h>
using namespace std;
//线性筛质数
int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉
void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}
LL qmi(LL m, LL k, LL p)
{
    LL res = 1 % p, t = m;
    while (k)
    {
        if (k&1) res = res * t % p;
        t = t * t % p;
        k >>= 1;
    }
    return res;
}
int Get_Mingen(int p){//获得最小生成元
    for(int i=2;i<p;i++){
        int cnt=1;
        int tmp=i;
        while(tmp!=1){
            tmp=qmi(i,++cnt,p);
        }
        if(cnt==(p-1)){
            return i;
        }
    }
    return 0;
}
int main()
{
    int p;
    cin>>p;
    int Minimum_generator=Get_Mingen(p);
    cout<<p<<"的Zp*最小生成元是"<<Minimum_generator<<endl;
    get_primes(10000);
    int maxn=0,prime;
    for(int i=0;i<cnt;i++){
      if(Get_Mingen(primes[i])>maxn){
          prime=primes[i];
          maxn=Get_Mingen(primes[i]);
      }
    }
    cout<<"在1-10000中使Zp*最小生成元最大的素数是"<<prime<<endl;
}

运行结果如下：

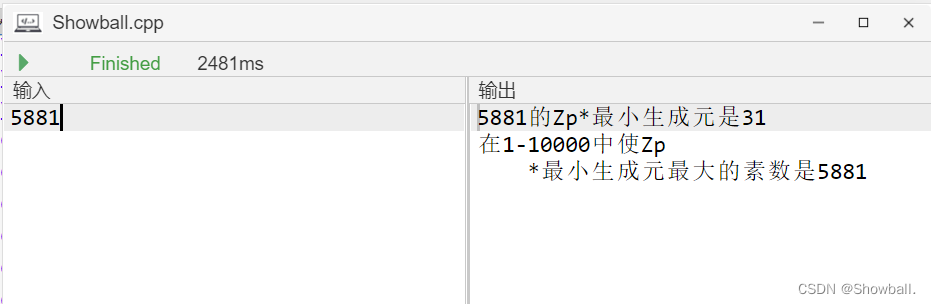
所以5881使Zp*的最小生成元最大，最大的最小生成元的31。

第8章

3.如果$\mathbb{G}$是群，$\mathbb{H}$是群$\mathbb{G}$的子群，且$[\mathbb{G}:\mathbb{H}]=2$，请证明对任意的$g\in \mathbb{G}$，$g\mathbb{H}=\mathbb{H}g$。

证明：因为$[\mathbb{G}:\mathbb{H}]=2$，所以$\mathbb{G}$被$\mathbb{H}$划分了两部分，我们设一部分为$\mathbb{H}$，一部分为$\mathbb{K}$。
当$g\in \mathbb{H}$时，则$g^{-1}\in \mathbb{H}$，那么$g\mathbb{H}{g}^{-1}$=$\mathbb{H}$。所以$g\mathbb{H}{g}^{-1}g$=$\mathbb{H}g$
当$g\notin \mathbb{H}$时,由于陪集性质，所以$g\mathbb{H}\ne \mathbb{H}$，$\mathbb{H}g\ne \mathbb{H}$
由于陪集的性质，$\mathbb{G}$被划分成两个部分，那么$g\mathbb{H}$和$\mathbb{H}g$只能属于另外一个部分，所以$g\mathbb{H}=\mathbb{H}g$。
综上，证毕！

4.设$\mathbb{G}$是阶为$pq$的群，其中$p$和$q$是素数。请证明$\mathbb{G}$的任意真子群是循环群。

证明：p,q是素数，所以pq的因子只有1，p，q，pq。根据拉格朗日定理，则其真子群的阶有1，p，q。
当真子群的阶为1时，即为平凡子群，真子群显然是循环群。
当真子群的阶为p，q时，根据拉格朗日定理的推论，素数阶数的有限群一定是循环群。
综上，证毕！

5.如果群$\mathbb{H}$是有限群$\mathbb{G}$的真子群，即存在$g\in \mathbb{G}$但是$g\notin \mathbb{H}$。请证明$|\mathbb{H}|\le |\mathbb{G}|/2$。