数据插值之朗格朗日插值（一）

锂享生活

已于 2024-05-25 16:42:51 修改

阅读量896

点赞数 28

文章标签：算法笔记

于 2024-05-25 16:41:51 首次发布

本文链接：https://blog.csdn.net/m0_63227758/article/details/139198246

版权

一、引言

二、代码实现

2.1 Lagrange插值求插值多项式：

2.2 Lagrange插值求新样本值和误差估计：

代码解析：

1.errorbar(x, y, R, '.g')

2.plot(X, Y, 'or')

三、Lagrange在Matlab中的使用模板

一、引言

数据插值是指通过有限个原始数据点构造出一个解析表达式，从而可以计算数据点之间的函数值。在Matlab中数据插值的方法主要有拉格朗日插值、牛顿差值、三次样条插值、埃尔米特插值、一维数据插值、二维数据插值等等。笔者旨在写一个使用Matlab进行数值插值的专题，通过介绍插值原理，代码实现，形成模板，方便日后使用时直接代入参数直接调用。

本节介绍拉格朗日插值（Lagrange interpolation）。Lagrange插值是一种用于逼近通过给定数据点的函数的方法。它涉及构造一个度数为 ( n-1 ) 或更低的多项式，该多项式通过 ( n ) 个给定点。该多项式是使用Lagrange基多项式构造的，这是一组多项式，当在给定点之一进行评估时，会得到1，并且当在任何其他给定点进行评估时会得到0。

Lagrange插值多项式可表示为：

$L(x) = \sum_{i=0}^{n} y_i l_i(x)$

Lagrange插值基函数可以表示为：

$l_i(x) = \frac{(x-x_0)(x-x_1)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_n)}{(x_i - x_0)(x_i - x_1)\cdots(x_i - x_{i-1})(x_i - x_{i+1})\cdots(x_i - x_n)}$

二、代码实现

2.1 Lagrange插值求插值多项式：

function[C, L, L1, l] = lagranl(X, Y)
% 定义拉格朗日插值多项式和基函数
%
% 输入:
%   X - 插值节点的横坐标向量
%   Y - 插值节点的纵坐标向量
%
% 输出:
%   C - 拉格朗日插值多项式的系数向量
%   L - 拉格朗日插值多项式的符号表达式
%   L1- 拉格朗日基函数对应的系数矩阵
%   l - 拉格朗日基函数对应的符号表达式

m = length(X); % 获取插值节点的个数

L1 = zeros(m, m); % 初始化存储拉格朗日基函数系数的矩阵
l = sym(zeros(1, m)); % 初始化单行符号值存储基函数表示式

for k = 1:m % 遍历每一个插值节点
    V = 1; % 初始化基函数的系数向量为1
    for i = 1 : m % 遍历所有节点用于计算
        if k ~= i %排除掉自身的情况
            V = conv(V, poly(X(i))) / (X(k) - X(i)); % 更新基函数的系数向量
        end
    end
    L1(k, :) = V; % 存储第k个基函数的系数
    l(k) = poly2sym(V) * Y(k); % 将基函数乘以对应的Y值，转换为符号表达式并存储
end

C = sum(Y .* L1, 1); % 计算拉格朗日插值多项式的系数向量
L = sum(l); % 计算拉格朗日插值多项式的符号表达式

下面进行测试：

X = [-2.2, -1.0, 0.01, 1.0, 2.0, 3.3, 2.2];
Y = [17.1, 7.3, 1.1, 2.0, 17.1, 23.1, 19.3];
[C, L, L1, l] = lagranl(X, Y);
L = vpa(L, 3)

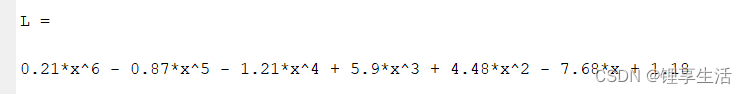
代码解析：

1.vpa解释

vpa 是 MATLAB 中的一个函数，表示 “Variable Precision Arithmetic”（可变精度计算）。在这个特定的调用中,vpa(L, 3) 将 L 的符号表达式以3位小数的精度表示。具体解释：

L: 是从 lagranl 函数中返回的拉格朗日插值多项式的符号表达式。
vpa(L, 3): 会将这个符号表达式的系数和结果值保留到小数点后3位。

假如：

L = sym('0.123456789*x^2 + 0.987654321*x + 3.141592653');

使用 vpa 后：

L = vpa(L, 3)
% 将变为
L = sym('0.123*x^2 + 0.988*x + 3.14');

2.ploy（x）解释:

在MATLAB中,ploy(x)函数并不是直接用来创建多项式的，容易与用于多项式插值的ployfit()或构造多项式系数的polyval()函数混淆。实际上，ploy(x)函数是用来从根求多项式的系数的。也就是说，如果你有一系列的复数或实数根,poly() 可以帮助你找到一个多项式，其在这些点上的值为零。

基本用法：

p = poly(r)

r 是一个向量，包含了多项式的根。
p 是返回的结果，是一个向量，表示对应于根 r 的多项式的系数，按降幂排列。

举个例子：

r = [1, 2];
p = poly(r);
disp(p);  % 输出多项式系数

这段代码会输出 [1 -3 2]，对应于多项式 $x^2-3x+2$ ，验证了1和2确实是这个多项式的根。

3.conv（）解释

conv是MATLAB 中用来执行多项式卷积（Convolution）的函数。在多项式运算中，conv 可以用来计算两个多项式的乘积。

基本用法

C = conv(A, B)

其中 A 和 B 是两个多项式的系数向量，返回向量 C 表示这两个多项式的乘积的系数。

示例：

假设我们有两个多项式：

$P(x) = 1 + 2x + 3x^2$

$Q(x) = 4 + 5x$

用系数向量表示：

P = [3, 2, 1]; % 对应： $1 + 2x + 3x^2$
Q = [5, 4]; % 对应： $5x + 4$

我们使用conv来计算两者的乘积：

P = [3, 2, 1];  % 3x^2 + 2x + 1
Q = [5, 4];     % 5x + 4

C = conv(P, Q)

% 输出 C
% C = [15 22 13 4] 对应最终方程式：15x^3 + 22x^2 + 13x + 4

4.poly2sym()解释

poly2sym()是把多项式系数转换为符号多项式。

$V = [1, 2, 3]\rightarrow x^2+3x+2$

2.2 Lagrange插值求新样本值和误差估计：

%% 拉格朗日插值及误差估计
% 此函数使用拉格朗日插值公式来计算插值值，并估计误差
% 输入参数:
% X - 已知数据点的x坐标 (向量)
% Y - 已知数据点的y坐标 (向量)
% x - 需要插值的x坐标 (向量)
% M - 最大连续(n+1)阶导数的上界 (标量)
% 输出参数:
% y - 插值后的y值 (向量)
% R - 误差估计 (向量)

function [y, R] = lagranzi(X, Y, x, M)
    n = length(X);      % 已知数据点的数量
    m = length(x);      % 需要插值的数据点数量

    for i = 1:m
        z = x(i);       % 当前需要插值的x坐标
        s = 0.0;        % 插值和初始化为0

        for k = 1:n
            p = 1.0;    % 插值多项式L_k(z)初始化为1
            q1 = 1.0;   % 误差估计中的分子初始化为1
            c1 = 1.0;   % 误差估计中的分母初始化为1

            for j = 1:n
                if j ~= k
                    % 计算拉格朗日基函数L_k(z)
                    p = p * (z - X(j)) / (X(k) - X(j));
                end
                % 计算误差估计的分子部分
                q1 = abs(q1 * (z - X(j)));
                % 计算误差估计的分母部分
                c1 = c1 * j;
            end
            
            % 加权求和得到插值值
            s = p * Y(k) + s;
        end
        
        y(i) = s;         % 存储插值结果
        R(i) = M * q1 / c1;  % 计算并存储误差估计
    end
end

下面进行测试：

clc
clear
X = [-2.2, -1.0, 0.01, 1.0, 2.0, 3.3, 2.2];
Y = [17.1, 7.3, 1.1, 2.0, 17.1, 23.1, 19.3];
x = linspace(-3, 4, 50);
M = 1;
[y, R] = lagranzi(X, Y, x, M);
errorbar(x, y, R, '.g')
hold on
plot(X, Y, 'or')
x = 2.8;
[y, R] = lagranzi(X, Y, x, M);
x = -3:0.01:4;
L = 0.21*x.^6 - 0.87*x.^5 - 1.21*x.^4 + 5.9*x.^3 + 4.48*x.^2 - 7.68*x + 1.18;
plot(x, L)
legend('误差', '样本点', '拉格朗日多项式函数曲线')
print(gcf, '-r600', '-djpeg', '图2-1.jpg')

代码解析：

1.errorbar(x, y, R, '.g')

在MATLAB中，errorbar() 函数用于绘制带有误差条的图形，它能够直观地展示数据点的不确定度或误差范围。函数调用格式中的各个参数含义如下：

errorbar(x, y, R, '.g')

这里各参数的含义是：

x：数据点，在x轴上的值。
y：数据点，与x对应，在y轴上的值。
R：这可以是一个向量或一个矩阵，定义了误差条的长度。如果是向量，那么这个向量提供了每个数据点y方向上的误差估计；如果是矩阵（通常是2列），第一列是负方向的误差，第二列是正方向的误差，用于分别表示y值的下限和上限。
'.'：这是一个标记符号参数，指定了数据点的样式，在这个例子中使用的是点。
'g'：颜色代码，指定了数据点和误差条的颜色，在这里是绿色。

2.plot(X, Y, 'or')

'o' 表示数据点将以圆圈形式标记。如果只用 'o'，MATLAB 会在每个 (X, Y) 数据对的位置绘制一个空心的圆圈。
'r' 表示红色（red）。结合前面的 'o'，这意味着每个数据点将以红色填充的圆圈来表示。

三、Lagrange插值使用模板

如果目前你拥有X,Y样本点，仅想求出一个新的x所对应的y值，可以直接在下述代码中进行修改“示意用法”中的值，程序放入Matlab中可以直接执行：

clc
clear
% 示例用法
x = [1, 2, 3, 4];
y = [1, 4, 9, 16];
xi = 2.5;
L_value = lagrange_interpolation(x, y, xi);
disp(['在 xi = ' num2str(xi) ' 处的插值值是 ' num2str(L_value)]);

function L = lagrange_interpolation(x, y, xi)
    % 拉格朗日插值函数
    % x 和 y 是已知的数据点
    % xi 是希望插值的点
    % 返回的 L 是在 xi 处的插值结果
    
    % 确保 x 和 y 长度一致
    if length(x) ~= length(y)
        error('x 和 y 必须具有相同的长度');
    end
    
    % 初始化结果 L
    n = length(x);
    L = 0;
    
    % 计算拉格朗日多项式
    for i = 1:n
        % 初始化基多项式
        Li = 1;
        for j = 1:n
            if i ~= j
                Li = Li * (xi - x(j)) / (x(i) - x(j));
            end
        end
        % 累加到结果
        L = L + Li * y(i);
    end
end

参考资料：《Matlab编程与汽车仿真应用》 ——崔胜民

锂享生活

关注

28
点赞
踩
30

收藏

觉得还不错? 一键收藏
0
评论
数据插值之朗格朗日插值（一）

笔者旨在写一个使用Matlab进行数值插值的专题，通过介绍插值原理，代码实现，形成模板，方便日后使用时直接代入参数直接调用。该多项式是使用Lagrange基多项式构造的，这是一组多项式，当在给定点之一进行评估时，会得到1，并且当在任何其他给定点进行评估时会得到0。也就是说，如果你有一系列的复数或实数根,poly() 可以帮助你找到一个多项式，其在这些点上的值为零。，容易与用于多项式插值的ployfit()或构造多项式系数的polyval()函数混淆。Q = [5, 4];表示这两个多项式的乘积的系数。
复制链接

扫一扫