机器学习之——支持向量机

最新推荐文章于 2024-06-13 19:02:31 发布

榆树花

最新推荐文章于 2024-06-13 19:02:31 发布

阅读量915

点赞数 20

文章标签：机器学习支持向量机人工智能

本文链接：https://blog.csdn.net/m0_63916929/article/details/135070534

版权

支持向量机（SVM）

一、SVM概述

支持向量机是一种常用的监督学习算法，主要用于分类和回归问题。它的核心思想是找到一个最优的超平面，将不同类别的样本点有效地分开，同时尽量使得分类边界与样本点之间的间隔最大化。

具体来说，支持向量机的基本概念包括以下几个要点：

超平面：在二维空间中，超平面就是一条直线；在三维空间中，超平面是一个平面。对于高维空间，超平面是一个（n-1）维的子空间。在支持向量机中，我们的目标就是找到一个超平面，能够将不同类别的样本点分开。
支持向量：支持向量是距离超平面最近的样本点，它们决定了超平面的位置和方向。也就是说，支持向量是离分类边界最近的样本点。
间隔：支持向量机追求的是使分类边界与样本点之间的间隔最大化。这个间隔被称为“间隔最大化”，是支持向量机的一个重要特点。
核函数：当数据集在低维空间中无法线性可分时，可以使用核函数将原始样本投影到更高维的空间中，使得分类问题在高维空间变成线性可分。常用的核函数包括线性核、多项式核和高斯核等。
优化算法：支持向量机的训练过程可以表示为一个凸优化问题，通过求解对应的拉格朗日乘子，可以得到最优的超平面。常用的优化算法包括梯度下降、SMO算法等。

二、SVM内容大纲

1.超平面

对于2分类的逻辑回归而言，假设特征数为2，那么我们训练模型的过程通过梯度下降不断更新参数迫近全局最优解，拟合出一条直线作为决策边界，使得以这个决策边界划分出来的分类结果误差最低。

当特征数量超过2，这个时候我们用来分割不同类别的“线”就成为了一个面，简称超平面（hyperplane），超即是多维的意思（二维就是一条线，三维就是一个面，多维就是超平面）。划分超平面可用如下线性方程表示：
$w^T x_i + b = 0$

其中 $w = (w1,w2,...,wd)^T$ 是法向量，b是位移。

如果我们用一条直线来将两种类别分开，如下图，可以看到有多条直线可以选择。

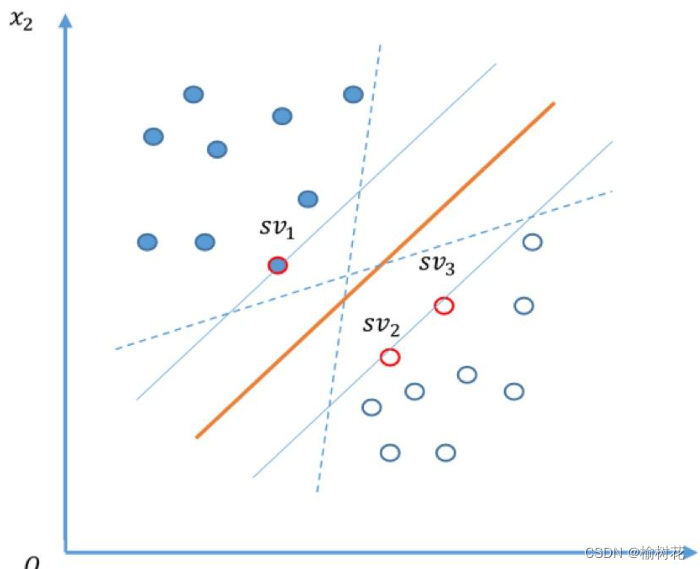
我们可以很直观的看出选择红色这条直线会具有更大的泛化能力，感觉它是最能分开这两类的直线，红色的这条决策边界就是通过间隔最大化求得的。

2.支持向量和决策边界

支持向量：在支持向量机中，支持向量是距离分类超平面最近的样本点。这些样本点位于间隔边界上或在错误分类一侧。支持向量决定了分类超平面的位置和方向。只有支持向量的位置发生变化时，分类超平面才会改变。

决策边界：决策边界是支持向量机分类超平面的表示。对于二分类问题，决策边界是一个超平面，可以将样本空间分割成两个不同的类别。在二维特征空间中，决策边界通常是一条直线；在三维特征空间中，决策边界通常是一个平面。对于高维特征空间，决策边界是一个超平面。

分类结果：根据样本点在决策边界的位置，我们可以确定其分类结果。如果样本点位于决策边界的一侧，它将被分类为一个类别；如果样本点位于决策边界的另一侧，它将被分类为另一个类别。支持向量机通过最大化间隔来使分类结果更加准确。

总结起来，支持向量是离分类超平面最近的样本点，它们决定了分类超平面的位置和方向。决策边界是支持向量机分类超平面的表示，它将样本空间分割成两个不同的类别。分类结果根据样本点在决策边界的位置确定。

3.间隔

支持向量机追求的是使分类边界与样本点之间的间隔最大化。这个间隔被称为“间隔最大化”，是支持向量机的一个重要特点。

间隔最大化

1.构建优化问题：

首先，我们要定义一个目标函数，将间隔最大化转化为一个优化问题。我们的目标是找到一组参数 (w) 和 (b)，使得间隔最大化。因此，我们可以定义目标函数如下：

间隔最大化= $[\arg\max_{w, b} \left(\frac{1}{|w|}\min_{i}(y_i(w^T x_i + b))\right) ]$

其中，(|w|) 表示向量 (w) 的范数，(y_i) 是样本 (x_i) 的标签。

2.转化为约束条件：

为了方便求解，我们通常会将目标函数转化为约束条件。在间隔最大化问题中，我们需要满足以下约束条件：

$[ y_i(w^T x_i + b) \geq 1, \quad \forall i ]$

这个约束条件表示所有样本点都应该位于两个超平面的间隔之外，并且离超平面的距离至少为1。

3.求解优化问题：

接下来，我们可以使用优化方法（如支持向量机）来求解上述优化问题，找到最优的参数 (w) 和 (b)，使得间隔最大化。

这个过程涉及到具体的数值计算和优化算法，可以使用数值计算库如scikit-learn或者数学建模软件如MATLAB进行求解。

总结起来，计算间隔最大化的过程就是将间隔最大化问题转化为一个优化问题，并利用合适的优化方法求解最优解。

4.核函数与非线性转换

（1）核函数

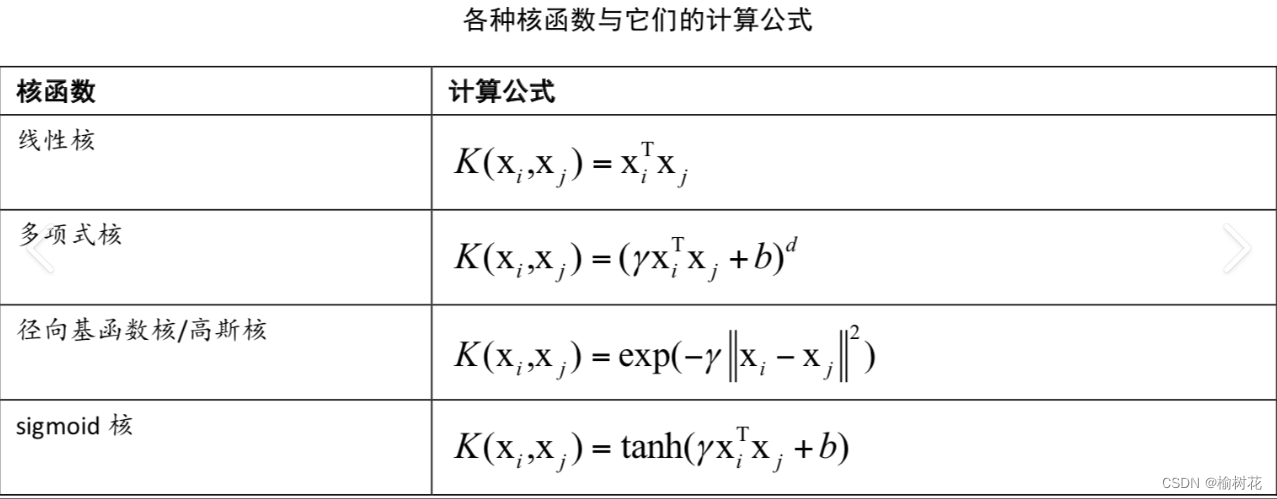
核函数是一种用于计算高维空间中两个向量之间内积的函数。它可以将原始的输入数据通过非线性映射转化到高维空间中，从而使得在低维空间中难以分离的样本在高维空间中容易被分离。通常情况下，我们不需要显式地计算高维空间中的内积，而是采用核函数来实现。在支持向量机中，常见的核函数包括线性核、多项式核、径向基核等。

常用的核函数包括线性核、多项式核和高斯核等。

线性核：线性核是最简单的核函数之一，它可以用于线性可分的问题。其定义如下： K(x, y) = x^T * y
多项式核：多项式核可以用于解决不完全线性可分的问题，它将样本映射到一个更高维的空间中，从而使得问题变成线性可分的。其定义如下： K(x, y) = (x^T * y + c)^d 其中，c是一个常数，d是多项式的次数。
高斯核：高斯核也被称为径向基函数（Radial Basis Function, RBF），它是一种常用的核函数。高斯核将样本映射到一个无限维的空间中，其定义如下： K(x, y) = exp(- ||x - y||^2 / 2 * sigma^2) 其中，sigma是一个控制高斯核宽度的参数。

以下是核函数的具体步骤：

(1) 选择合适的核函数：在使用支持向量机进行分类之前，我们需要选择一个合适的核函数。这个选择取决于我们所面临的问题类型以及数据集的特征。

(2) 计算核函数值：对于每一对样本之间的向量，我们需要计算它们在高维空间中的内积，即通过核函数计算它们的相似度。这个过程可以通过坐标变换和计算内积来实现。

(3) 构建核矩阵：将每个样本之间的核函数值存储在一个矩阵中，称为核矩阵。这个矩阵用于支持向量机的求解过程。

（2）非线性转换

非线性转换是指将原始输入数据通过非线性映射转化到高维空间中，从而使得在低维空间中难以分离的样本在高维空间中容易被分离。在支持向量机中，非线性转换通常通过核函数来实现。

以下是非线性转换的具体步骤：

(1) 选择合适的核函数：同样，在进行非线性转换之前，我们需要选择一个合适的核函数。

(2) 计算高维特征空间：对于每个输入样本，我们需要通过核函数计算它在高维特征空间中的向量。这个过程可以看作是对输入数据进行非线性映射。

(3) 训练支持向量机：在高维特征空间中，我们可以使用支持向量机来训练模型并进行分类。在训练过程中，我们将使用核函数来计算样本之间的内积，从而避免了进行显式的特征转换。

5.软间隔与松弛变量

（2）软间隔

在传统的支持向量机中，我们假设所有的样本都是线性可分的，即存在一个超平面可以完全将正负样本分离。但是在实际应用中，很多情况下样本并不是线性可分的，这时候我们就需要引入软间隔的概念。所谓软间隔，就是允许一些样本点不满足约束条件，而是允许它们有一定的误差。

如下图中一些软间隔划分的区域中是允许出现由蓝球出现在粉球这一侧的误差出现。

软间隔的具体步骤如下：

(1) 引入松弛变量：为了允许一些样本点不满足约束条件，我们引入一个松弛变量 ξi，表示第 i 个样本点到超平面的距离。

(2) 修改目标函数：在传统的支持向量机中，目标函数是 $\min_{w,b} \frac{1}{2} ||w||^2$ ，表示最小化模长。在软间隔中，我们需要修改目标函数为 $\min_{w,b} \frac{1}{2} ||w||^2 + C \sum_{i=1}^m \xi_i$ ，其中 C 是一个调整正则化和误差之间权重的参数。

(3) 约束条件修改：同时，我们需要将原来的约束条件 $y_i (w^T x_i + b) \geq 1$ 修改为 $1 - \xi_i \leq y_i (w^T x_i + b) \leq 1 - \xi_i$ ，这样就允许一些样本点不满足约束条件。

（2）松弛变量

松弛变量是软间隔中的一个概念，它用来表示样本点到超平面的距离。在传统的支持向量机中，所有的样本点都必须满足约束条件 $y_i (w^T x_i + b) \geq 1$ ，即到超平面的距离必须大于等于 11。但是在实际应用中，很多情况下样本并不是线性可分的，这时候我们就需要引入松弛变量。

具体来说，松弛变量 ξi 表示第 i 个样本点到超平面的距离，因此 1−ξi 表示该点到超平面的距离必须大于等于 11，ξi 则表示该点到超平面的距离小于 11，即该点分类错误。

在软间隔中，我们通过引入松弛变量来允许一些样本点不满足约束条件，从而实现对非线性可分问题的解决。

三、SVM应用

使用SVM算法对二维数据进行分类，并可视化分类结果

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.io import loadmat
from sklearn import svm

# 加载数据
raw_data = loadmat('data\ex6data1.mat')
data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])
data['y'] = raw_data['y'].flatten()

positive = data[data['y'] == 1]
negative = data[data['y'] == 0]

def plot_data(ax, X, y):
    '''绘制数据集的散点图'''
    ax.scatter(positive['X1'], positive['X2'], s=30, marker='x', label='Positive', c='black')
    ax.scatter(negative['X1'], negative['X2'], s=30, marker='o', label='Negative', c='y')
    ax.set_xlabel('x1')
    ax.set_ylabel('x2')
    ax.set_title('Example Dataset 1')
    ax.legend()

def plot_boundary(ax, clf, X):
    '''绘制超平面'''
    x_min, x_max = X[:, 0].min() * 1.2, X[:, 0].max() * 1.1
    y_min, y_max = X[:, 1].min() * 1.1, X[:, 1].max() * 1.1
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    ax.contour(xx, yy, Z)

# 将 DataFrame 转换为 NumPy 数组
X_np = data[['X1', 'X2']].values
y = data['y'].values

models = [svm.SVC(C=c, kernel='linear') for c in [1, 50, 100]]
clfs = [model.fit(X_np, y) for model in models]
titles = ['SVM Decision Boundary with C = {} (Example Dataset 1)'.format(c) for c in [1, 50, 100]]

for model, title in zip(clfs, titles):
    fig, ax = plt.subplots()
    plot_data(ax, X_np, y)
    plot_boundary(ax, model, X_np)
    ax.set_title(title)
    plt.show()

使用 loadmat 函数从文件中加载数据集 ex6data1.mat。将原始数据保存到 Pandas 的 DataFrame 中，并使用 Pandas 的一些函数对数据进行处理，例如将正负样本分别保存到 positive 和 negative 变量中。

定义 plot_boundary 函数：该函数用于绘制 SVM 模型的决策边界，使用 predict 方法获取预测值，并绘制出等高线图。

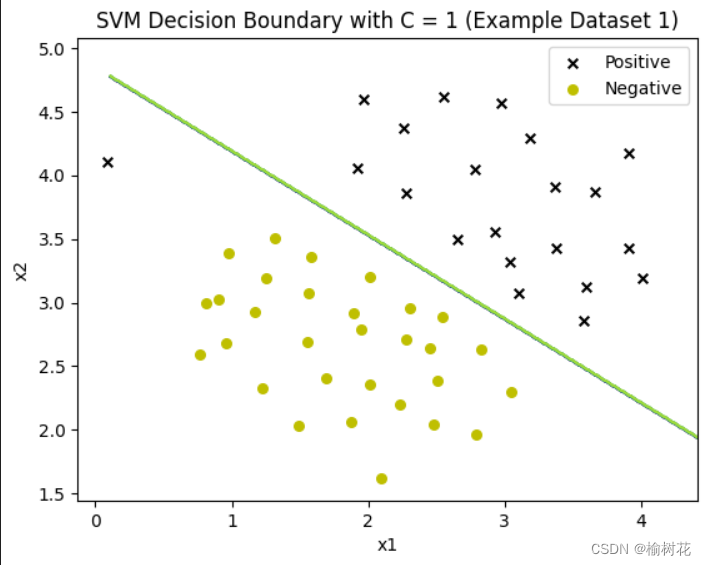
定义三个 SVM 模型，分别使用不同的正则化参数 C（1、50和100），并训练模型。

结果图：

# -*- coding: utf-8 -*-
import numpy as np
import pylab as plt
from sklearn import svm

X = np.r_[np.random.randn(20,2)-[2,2],np.random.randn(20,2)+[2,2]]
Y = [0] * 20+[1] * 20

clf = svm.SVC(kernel='linear')
clf.fit(X,Y)

w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5,5)
yy = a * xx - (clf.intercept_[0]) / w[1]  #(clf.intercept_[0])/w[1]指的是直线的截距

b = clf.support_vectors_[0]
yy_down = a * xx + (b[1] - a * b[0])#(b[1]-a*b[0])就是计算截距
b = clf.support_vectors_[-1]
yy_up = a * xx +(b[1] - a * b[0])

print("w:",w) #打印出权重系数
print("a:",a) #打印出斜率
print("suport_vectors_:",clf.support_vectors_)#打印出支持向量
print("clf.coef_:",clf.coef_)  #打印出权重系数

plt.figure()
plt.plot(xx,yy,'k-')
plt.plot(xx,yy_down,'k--') #绘制下边界
plt.plot(xx,yy_up,'k--') #绘制上边界
plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,0],s = 30,facecolors='none')
plt.scatter(X[:,0],X[:,1],c=Y,cmap=plt.cm.Spectral)
plt.axis('tight')
plt.show()

通过随机生成两组数据，分别属于两个类别。其中一组数据在坐标平面上的坐标值是从标准正态分布中随机生成的，并将其减去[2, 2]；另一组数据也是从标准正态分布中随机生成的，然后加上[2, 2]。这样生成的数据集就呈现出两个类别的聚类现象。然后，建立一个线性核函数的支持向量机分类器 svm.SVC(kernel='linear')，并将数据集X和对应的标签Y传入进行拟合。

获取分隔超平面的参数，其中包括权重系数w、斜率a以及截距。

计算并得出支持向量的方程，即确定了决策边界。通过支持向量的坐标和超平面的斜率计算得到下边界和上边界。

结果图：

四、实验小结

SVM 是一种强大的机器学习算法，主要用于二分类问题，但也可以扩展到多分类和回归问题。基本思想是通过在特征空间上找到一个最优的超平面，将不同类别的样本分开，并且使离超平面最近的样本点到该超平面的距离最大。核心概念是支持向量，它们是离超平面最近的训练样本点。这些支持向量决定了超平面的位置和形状。

SVM 可以使用不同的核函数，如线性核、多项式核和径向基函数（RBF）核，来处理线性不可分和非线性问题。训练过程涉及到选择适当的模型参数，如正则化参数 C 和核函数的参数。合理选择参数可以提高模型的泛化能力。

榆树花

关注

20
点赞
踩
14

收藏

觉得还不错? 一键收藏
1
评论
机器学习之——支持向量机

支持向量机是一种常用的监督学习算法，主要用于分类和回归问题。它的核心思想是找到一个最优的超平面，将不同类别的样本点有效地分开，同时尽量使得分类边界与样本点之间的间隔最大化。超平面：在二维空间中，超平面就是一条直线；在三维空间中，超平面是一个平面。对于高维空间，超平面是一个（n-1）维的子空间。在支持向量机中，我们的目标就是找到一个超平面，能够将不同类别的样本点分开。支持向量：支持向量是距离超平面最近的样本点，它们决定了超平面的位置和方向。也就是说，支持向量是离分类边界最近的样本点。间隔。
复制链接

扫一扫