【SPSS】列联表分析详细操作教程（附案例实战）

🤵‍♂️ 个人主页：@艾派森的个人主页

✍🏻作者简介：Python学习者
🐋 希望大家多多支持，我们一起进步！😄
如果文章对你有帮助的话，
欢迎评论 💬点赞👍🏻 收藏 📂加关注+

---

列联表分析

什么是列联表分析?

列联表分析也叫作交叉分组下的频数分析，用来分析变量间的相互影响和关系

 列联表分析的基本任务

• 编制交叉列联表
• 在交叉列联表的基础上，对两变量间是否存在一定的相关性进行分析

列联表的卡方检验

1.提出原假设（H0）

列联表分析中卡方检验的原假设是：行变量与列变量独立

2.计算检验统计量

列联表分析中卡方检验的检验统计量是Pearson卡方统计量，其数学定义为： 

 其中，r为列联表的行数；c为列联表的列数；fij o为观测频数； fij e为期望频数,期望频数的计算方法是：

 RT为指定单元格所在行的观测频数合计； CT为指定单元格所在列的观测频数合计； n为观测频数的总计；

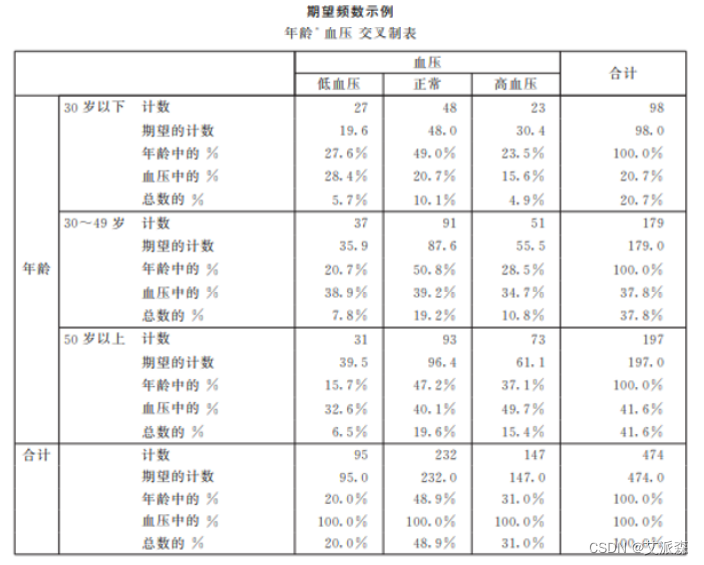
        例如：30岁以下且低血压组的期望频数为98x95/474=19.6, 其他单元格的期望频数相同的算法。 期望频数的分布反映的是行列变量独立下的分布。         

3.确定显著性水平和临界值

显著性水平α是指原假设为真却将其拒绝的风险，即弃真的概 率，通常设为0.05或0.01。在卡方检验中，由于卡方统计量服从 “（行数-1）x （列数-1）”个自由度的卡方分布，因此，在行列 数目和显著性水平α确定时，卡方临界值是唯一确定的。 

4.得出结论和决策

• 根据统计量观测值和临界值比较的结果进行决策 ：如果卡方统计量的观测值大于卡方临界值，则认为卡方值已经足够大，实际分布与期望分布之间的差距显著，可以拒绝原假 设，断定列联表的行列变量间不独立，存在相关关系
• 根据统计量观测值的概率P值和显著性水平α比较的结果进行决策：如果P值小于等于α，则拒绝原假设，断定列联表的行列变 量间不独立，存在相关关系

列联表卡方检验说明

• 如果交叉列联表中有较多单元格（20%以上）中的期望频数小于5，则一般不宜使用卡方检验。此 时，可以采用似然比卡方检验等方法进行修正
• 卡方值的大小也会受到样本量的影响，所以，也有必要对Pearson卡方值进行修正，以剔除样本量 的影响 

列联表分析案例 

【案例】 —— 影响高考志愿填报的因素与性别是否有关 

①选择菜单【分析】----> 【描述统计】----> 【交叉表】

②在“交叉表”对话框中选择行变量、列变量

③再点击上图（交叉表对话框）中的【单元格(E)】按钮，指定列联表单元格中的输出内容 

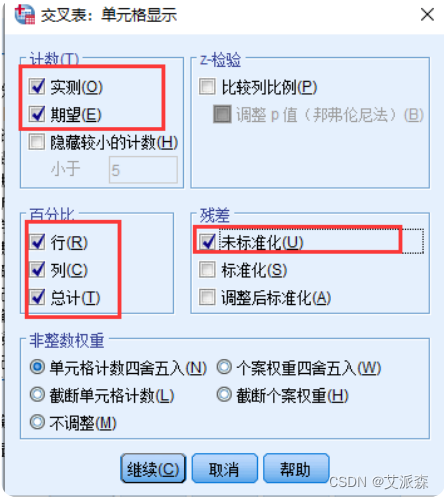
④点击交叉表对话框中的【统计(S)】按钮指定使用卡方检验来分析行变量和列变量间的关系 

⑤分析结果

结论：由于卡方的概率P值小于α，因此应拒绝原假设，认为不同性别的学生填报高考志愿时考虑的因素是不一致的。 

补充：

在卡方检验表中还出现了下面的两个卡方检验

• 似然比卡方检验，用于对Pearson卡方检验进行修正
• 线性关联卡方检验（Mantel-Haenszel），用于检验列联表中行列变量的线性相关性，原假 设是行列变量零相关，只适用于定序型变量，不能用于定类型变量