用于变分自动编码器（VAE）的 Copula 变分贝叶斯算法（Matlab代码实现）

然哥依旧

于 2024-10-11 12:00:00 发布

阅读量980

点赞数 10

文章标签：算法 matlab python

本文链接：https://blog.csdn.net/m0_64583023/article/details/142850506

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

2.1 高斯混合物的CVB：

2.2 双变量高斯的 CVB：

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

Copula 变分贝叶斯算法是一种结合了 Copula 函数和变分贝叶斯方法的算法，用于变分自动编码器 (VAE)。下面我将解释一下这个算法的基本思想和步骤。

首先，让我们回顾一下变分自动编码器 (VAE) 是如何工作的。VAE 是一种生成模型，通过学习输入数据的潜在分布来生成新的样本。它由两个部分组成：编码器和解码器。编码器将输入数据映射到潜在空间中的潜在变量，解码器根据潜在变量生成新样本。

然而，传统的 VAE 假设输入数据的潜在分布是多变量高斯分布。但在实际应用中，数据通常不满足高斯分布的假设。Copula 变分贝叶斯算法将 Copula 函数引入 VAE 中，以更好地建模数据的潜在分布。

Copula 函数是用于建立多变量分布的工具，它可以将边缘分布和相关性分离开来。Copula 函数的一个重要特性是它可以描述非线性相关性，因此可以更好地建模数据之间的复杂关系。

在 Copula 变分贝叶斯算法中，首先使用编码器将输入数据映射到潜在空间中，得到潜在变量的均值和方差。然后，使用 Copula 函数将潜在变量的边缘分布和相关性关系分离开来。具体地说，通过拟合 Copula 模型来建模潜在变量的相关性。

接下来，使用解码器根据潜在变量生成新样本。这里的关键是，解码器根据生成的潜在变量样本和 Copula 模型，通过反向变换来重构数据样本。

最后，在训练过程中，使用变分推断方法来估计潜在变量和模型参数的后验分布。这里的目标是最大化后验概率，从而优化模型的参数。

Copula 变分贝叶斯算法将 Copula 函数引入了 VAE 中，以更好地建模数据的潜在分布和相关性。通过将潜在变量的相关性关系分离开来，该算法可以更准确地生成新样本。

变分贝叶斯（VB），也称为独立平均场近似，已成为近年来贝叶斯网络推理的一种流行方法。它的应用非常广泛，例如在神经网络、压缩感知、聚类等方面。在本文中，VB 中的独立性约束将放宽为条件约束类，在统计学中称为 copula。由于联合概率分布始终属于 copula 类，因此新颖的 copula VB （CVB）近似是 VB 的广义形式。通过信息几何，我们将看到 CVB 算法迭代地将原始联合分布投影到 copula 约束空间，直到它达到局部最小 Kullback-Leibler （KL）散度。这样，所有均值场近似，例如迭代VB、期望最大化（EM）、迭代条件模式（ICM）和k均值算法，都是CVB近似的特例。对于通用贝叶斯网络，还将设计CVB的增强层次结构形式。虽然平均场算法只能返回相关网络的局部最优近似值，但增强型CVB网络是简单网络结构混合的最优加权平均值，可以首次实现全局最优近似。通过对高斯混合聚类的模拟，CVB的分类精度将远远优于最先进的VB、EM和k-means算法。

变分自动编码器是深度学习中用于估计权重的流行算法。尽管如此，VAE解只能通过随机梯度下降（SGD）方法找到。

除了使用梯度得体，我们还可以证明CVB算法可以应用于VAE问题，并直接产生迭代闭式解。由于 CVB 是平均场近似的一种松弛形式，因此 CVB 使用相同的易于处理的迭代方案，而不受变分贝叶斯方法等独立形式的限制。

此外，由于 CVB 是自由形式近似，因此 CVB 的形式可以自动迭代地适应真正的后验分布，直到收敛，而不受 VAE 等固定分布的约束。

最后，CVB方法的主要优点是CVB可以返回近似分布的最优混合。通过这种方式，我们可以将原始网络分解为近似网络的混合，其 CVB 的最优权重与每个近似网络的证据下限（ELBO）成正比。

📚2 运行结果

2.1 高斯混合物的CVB：

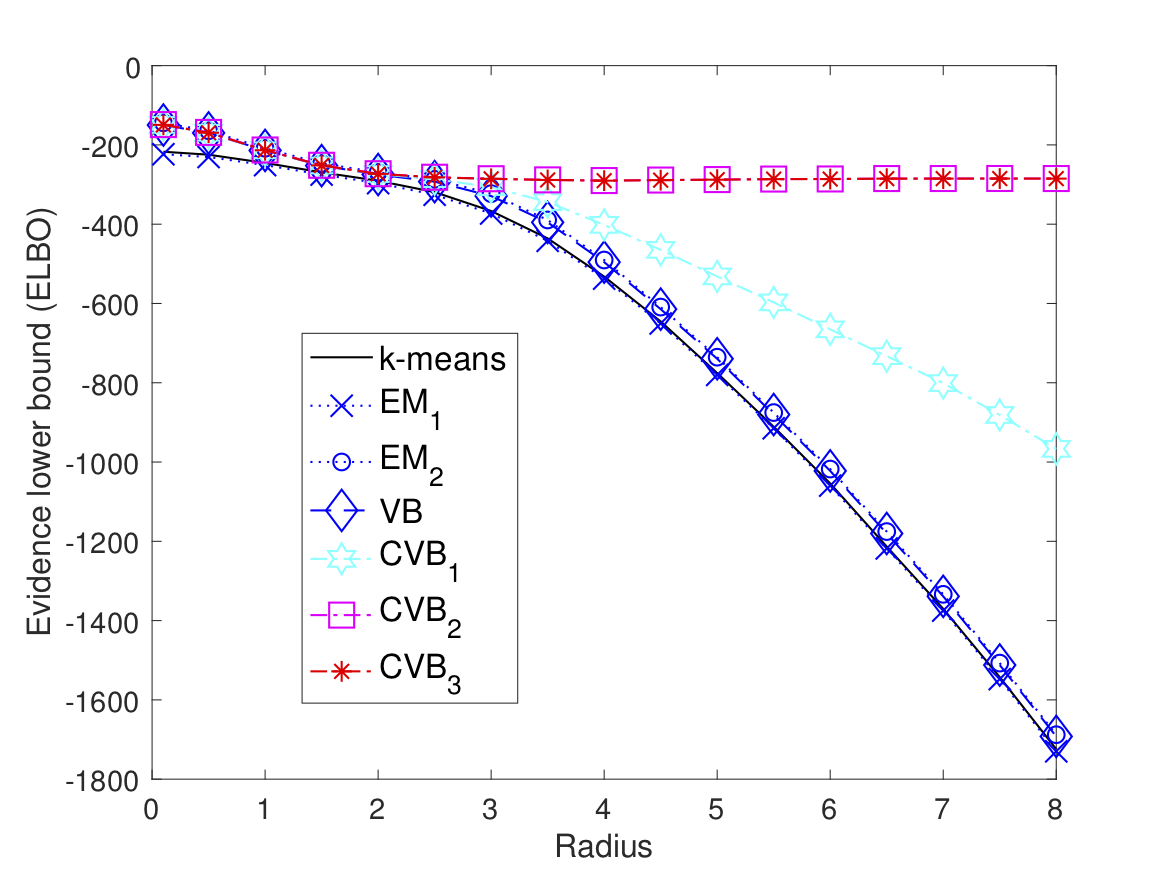
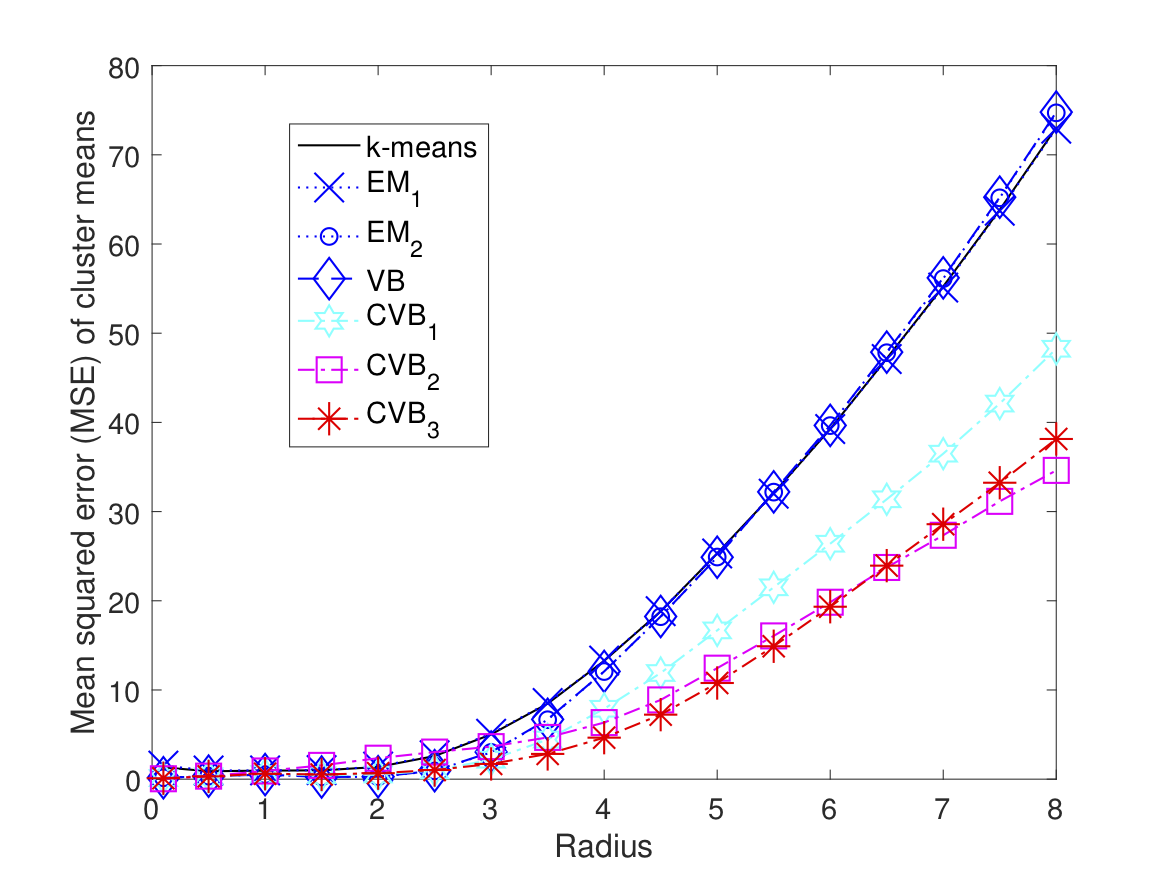
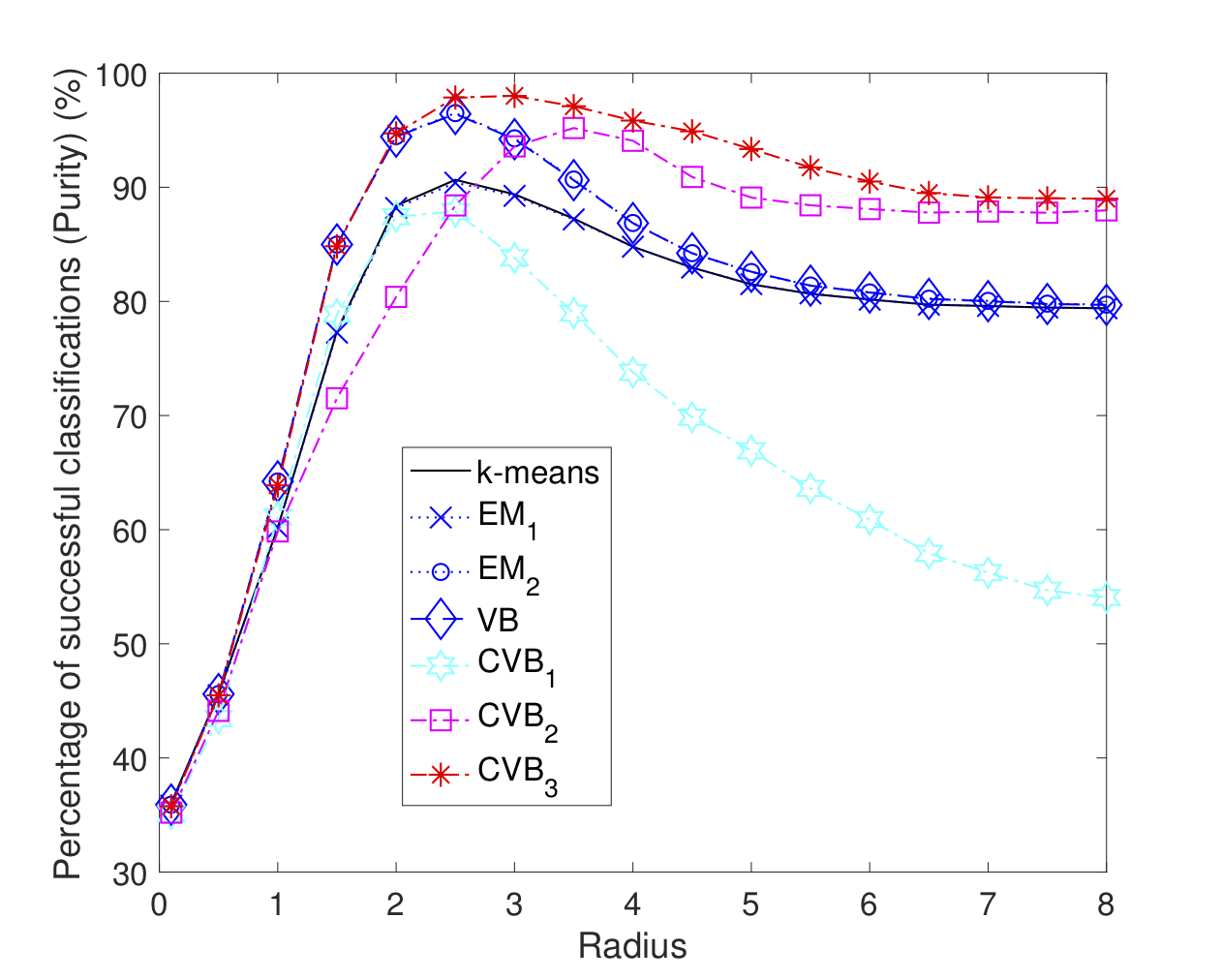
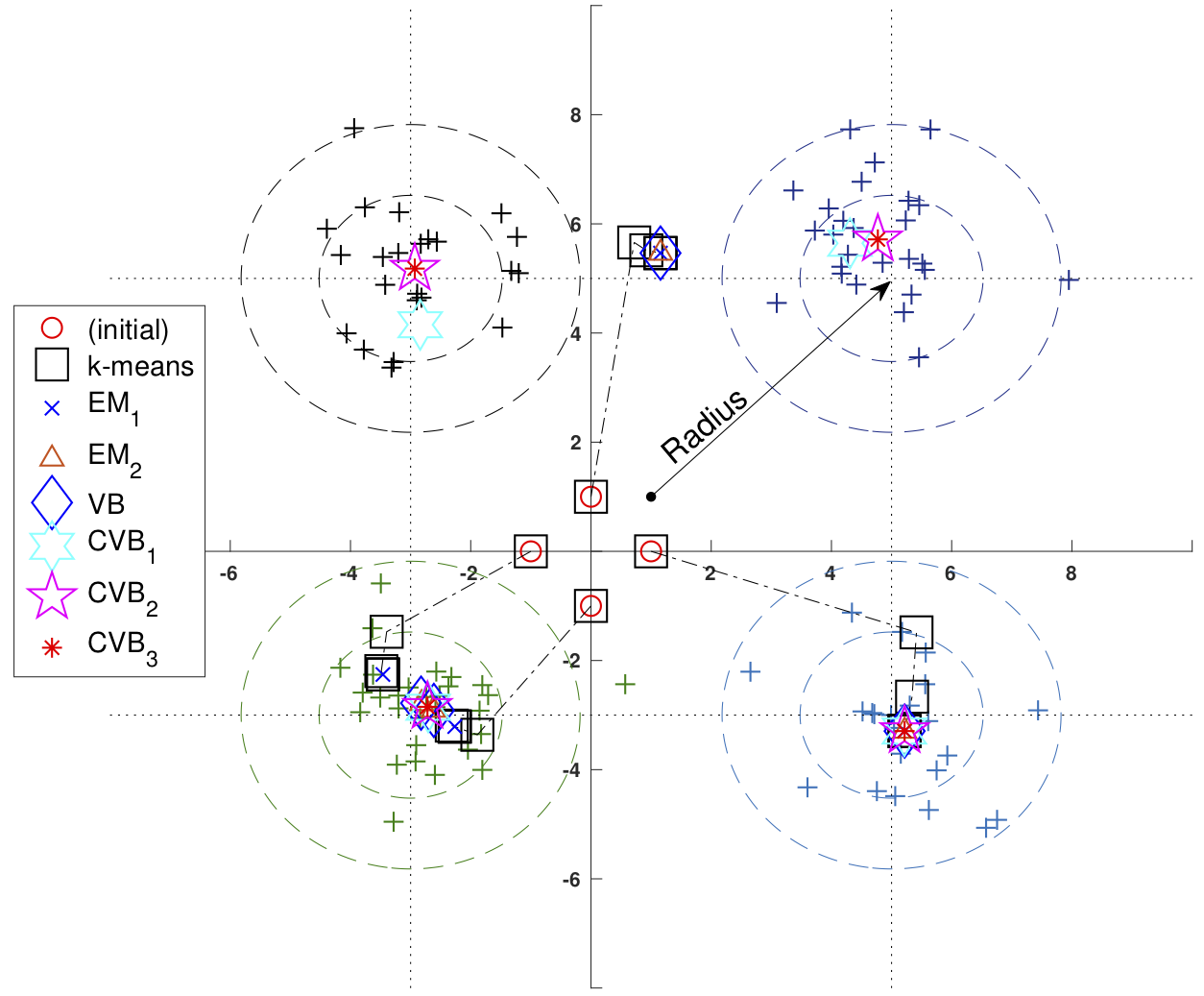
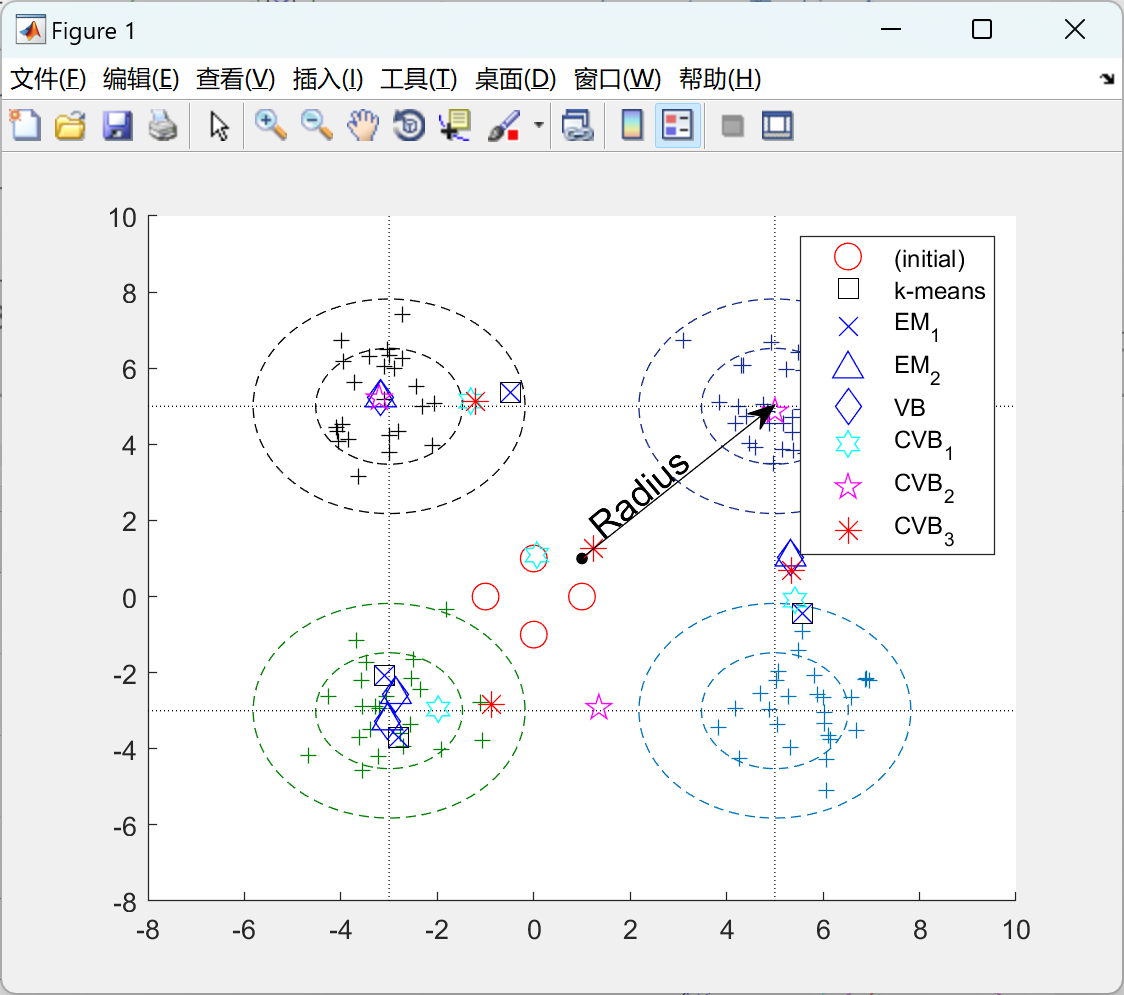
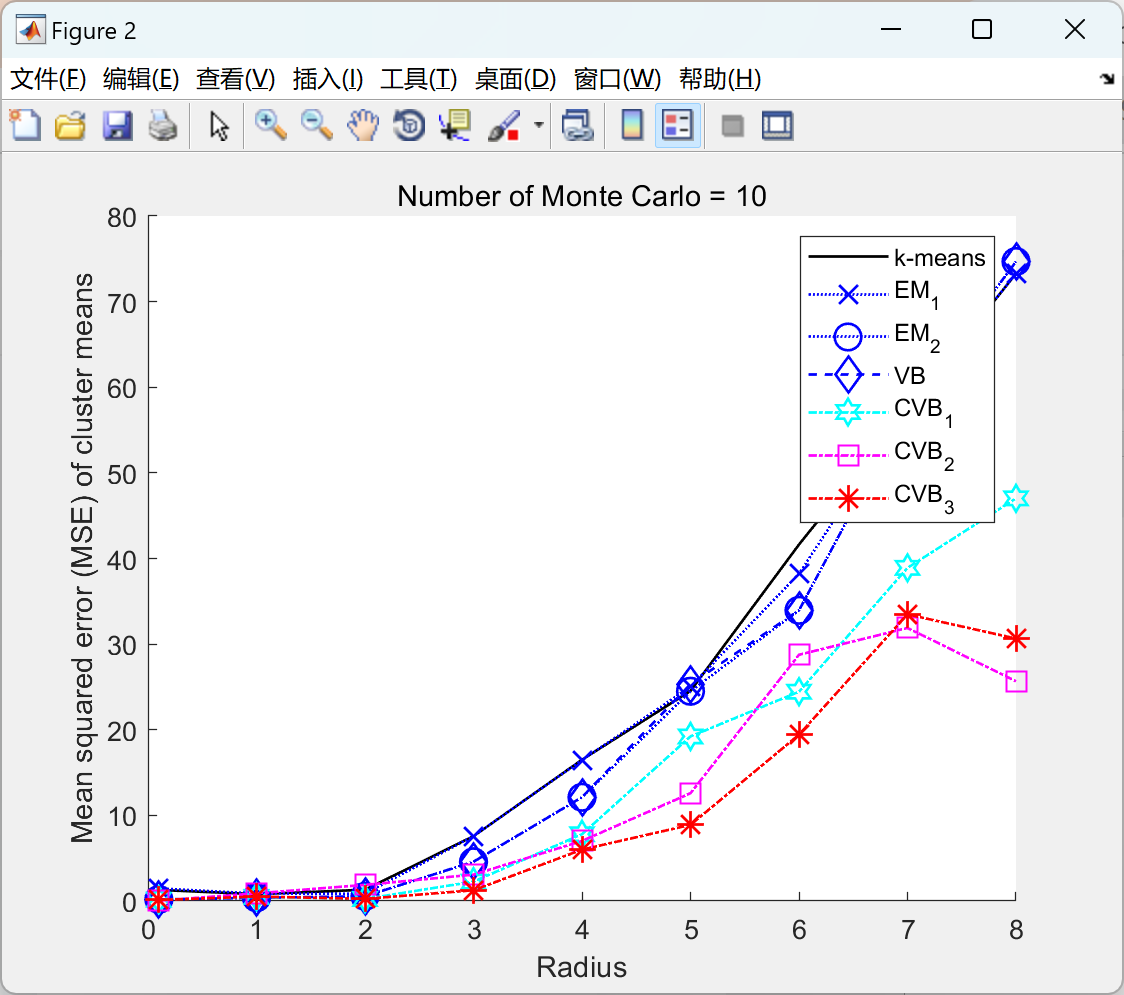
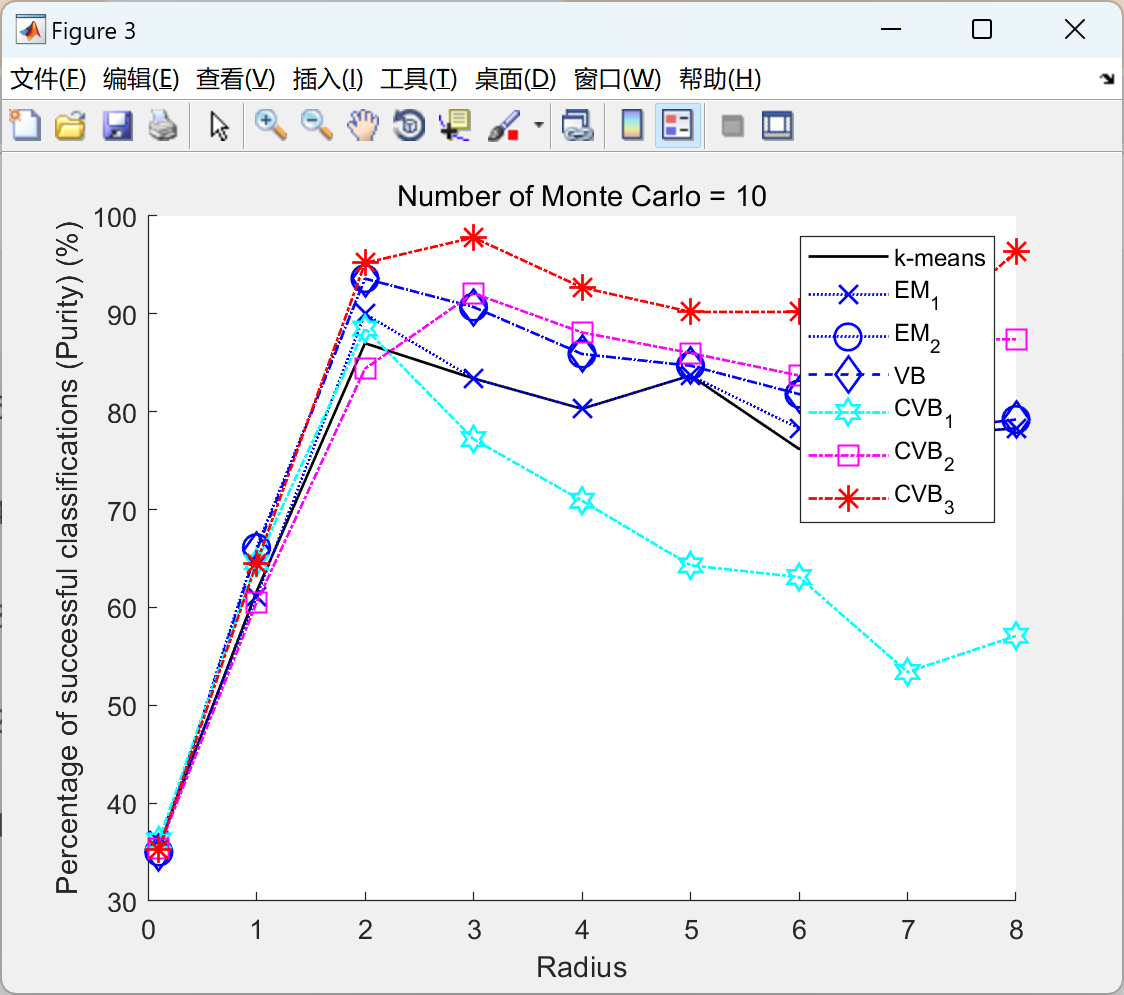
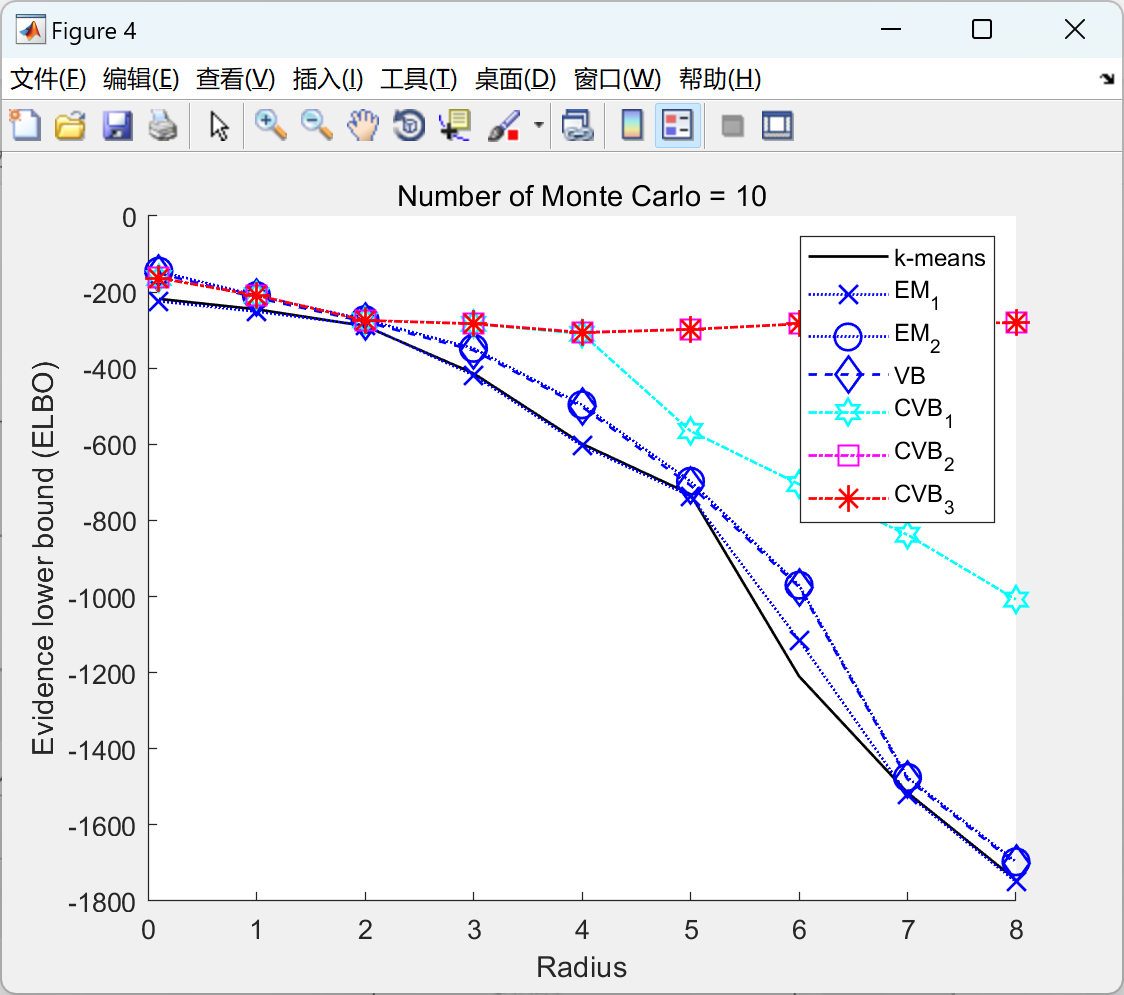
2.2 双变量高斯的 CVB：

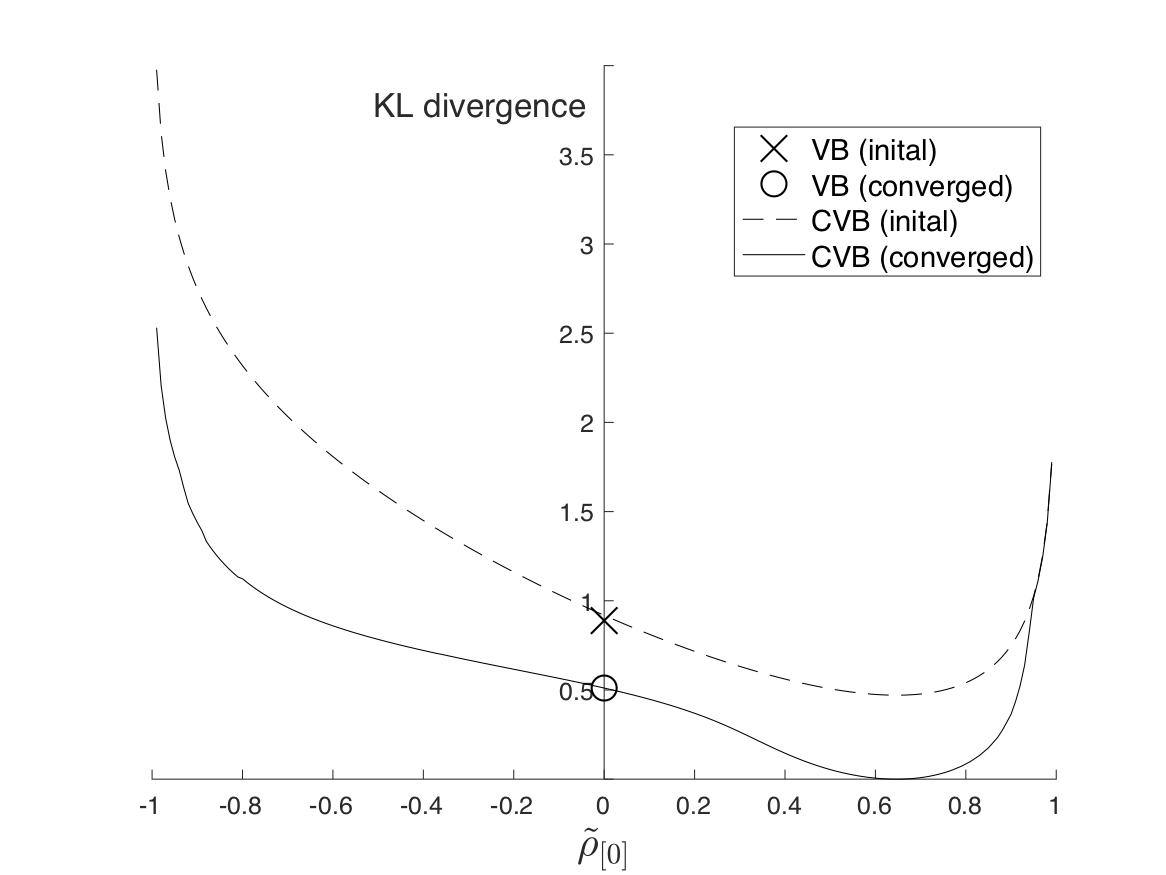
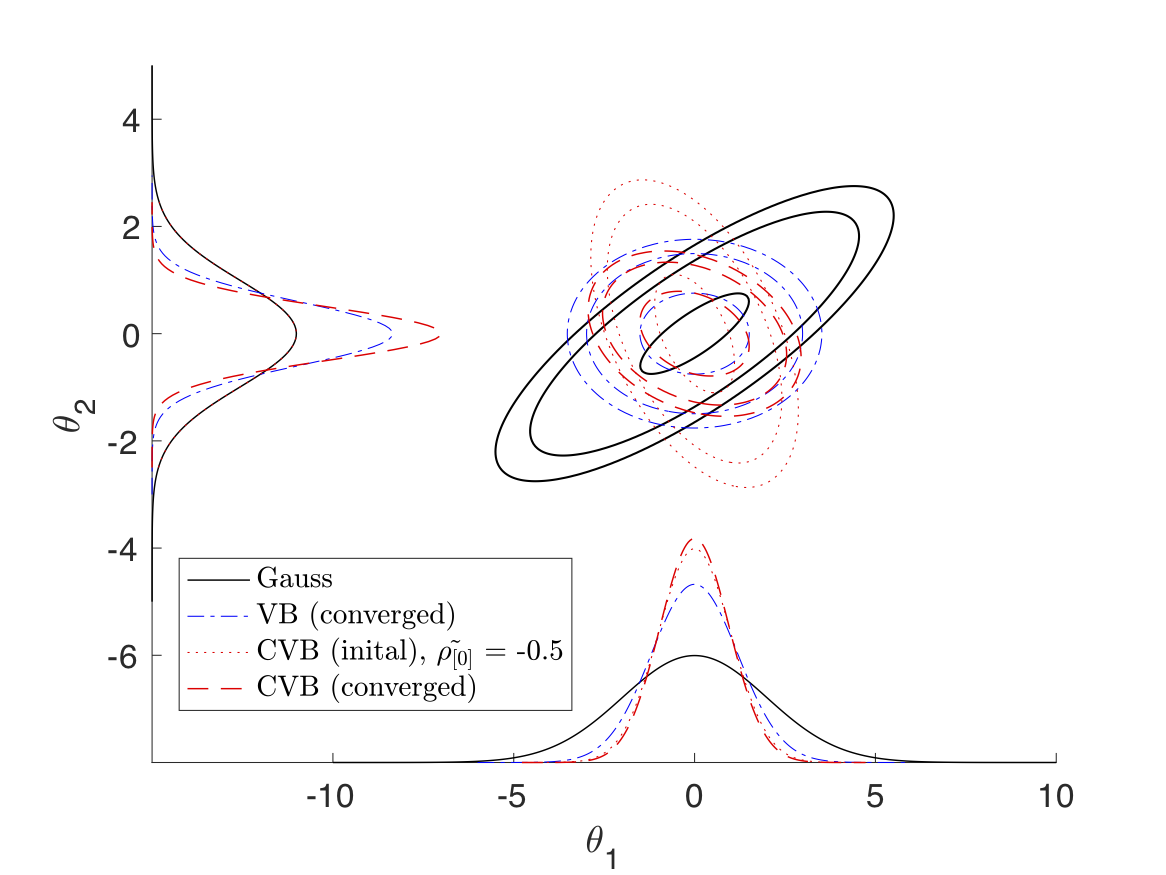
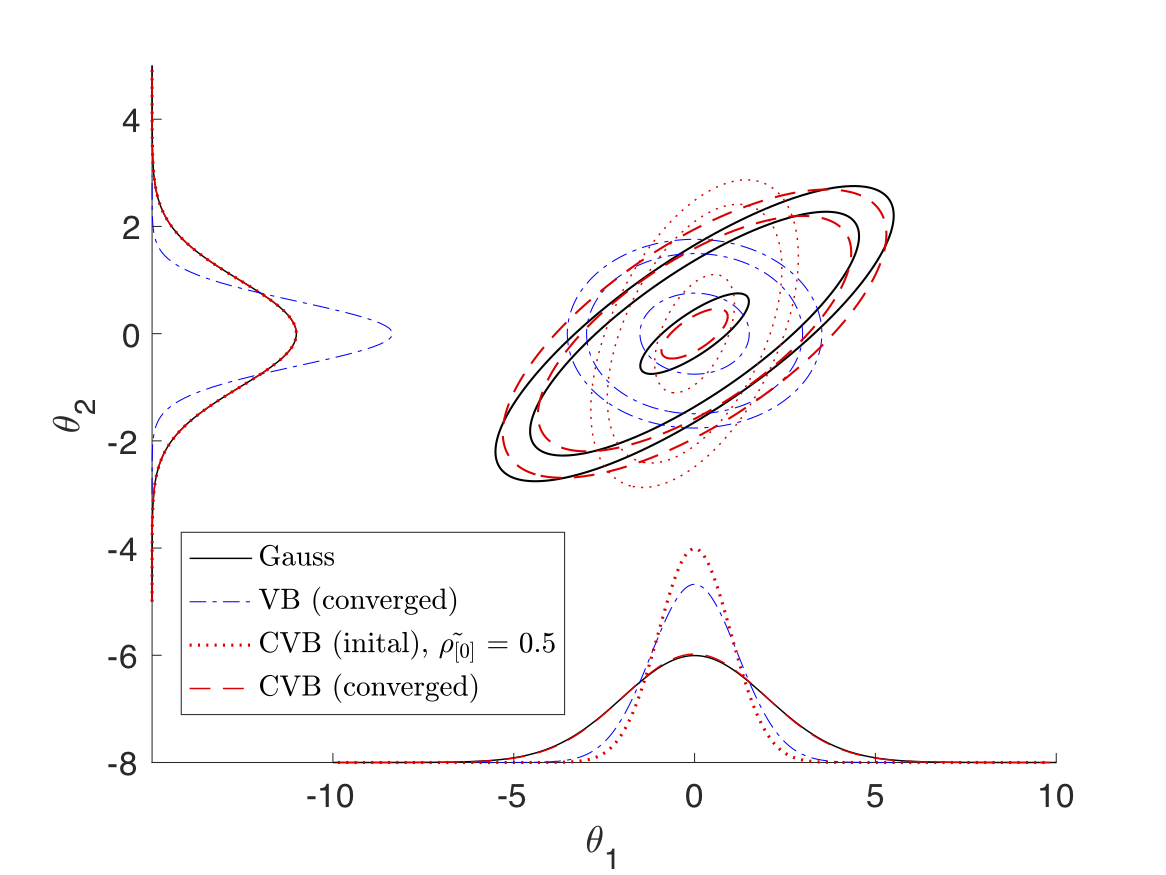
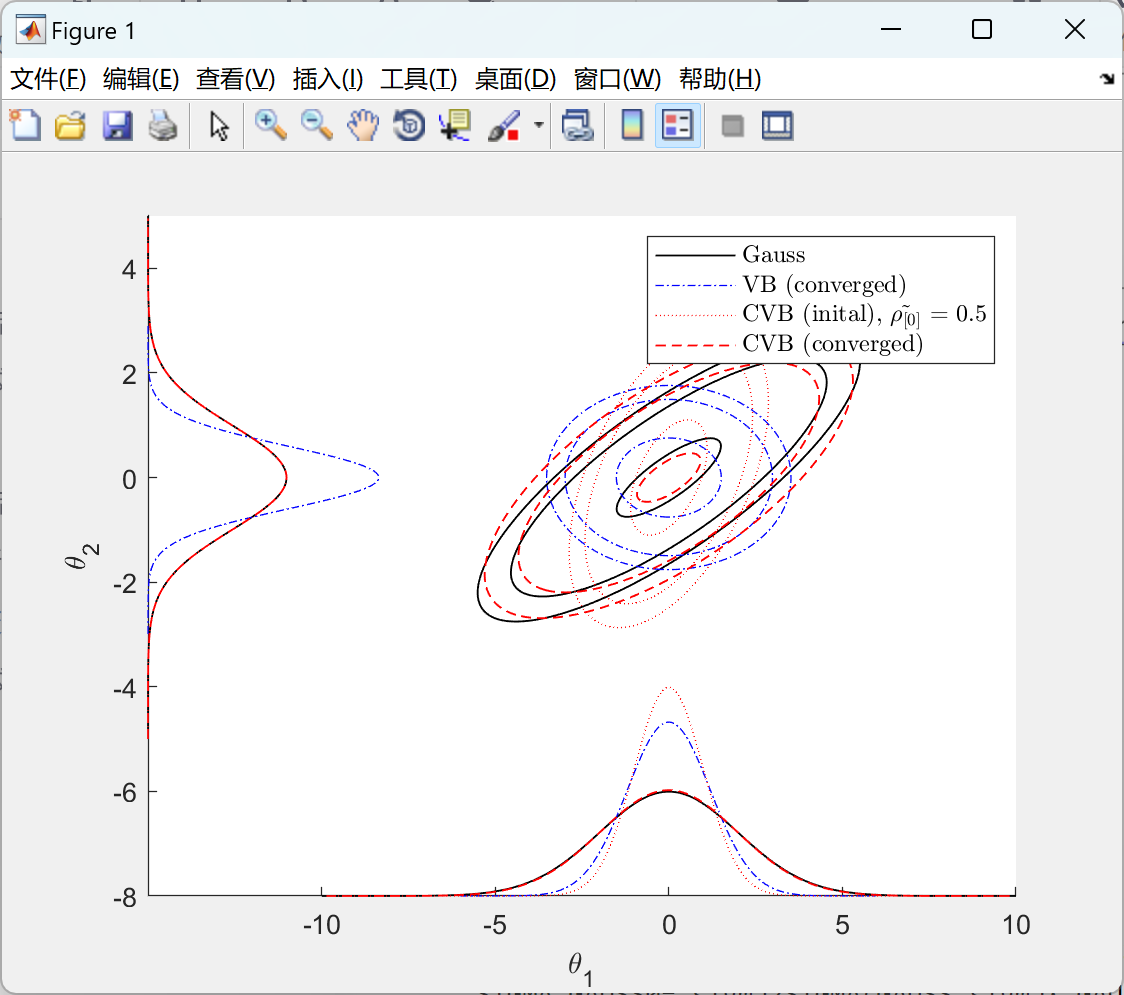
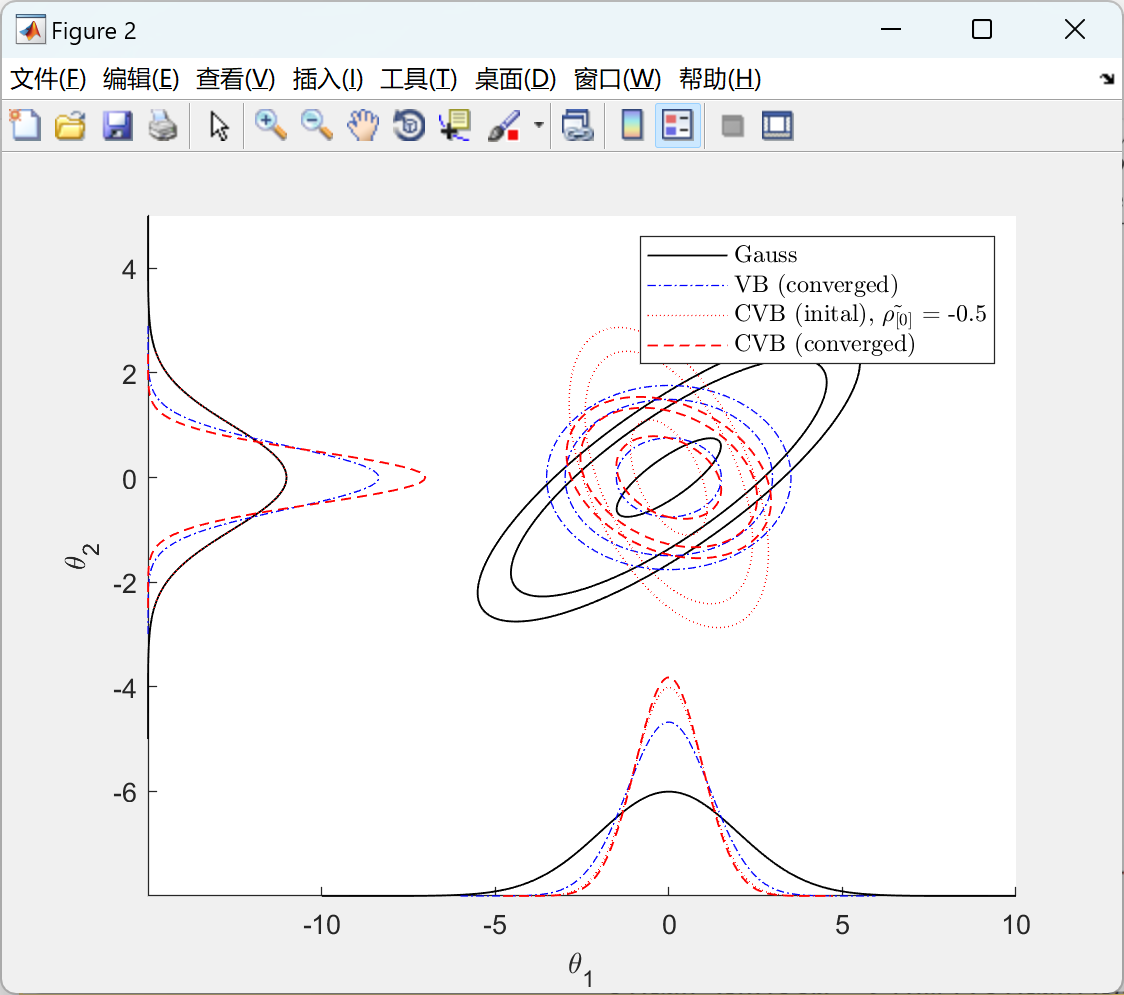
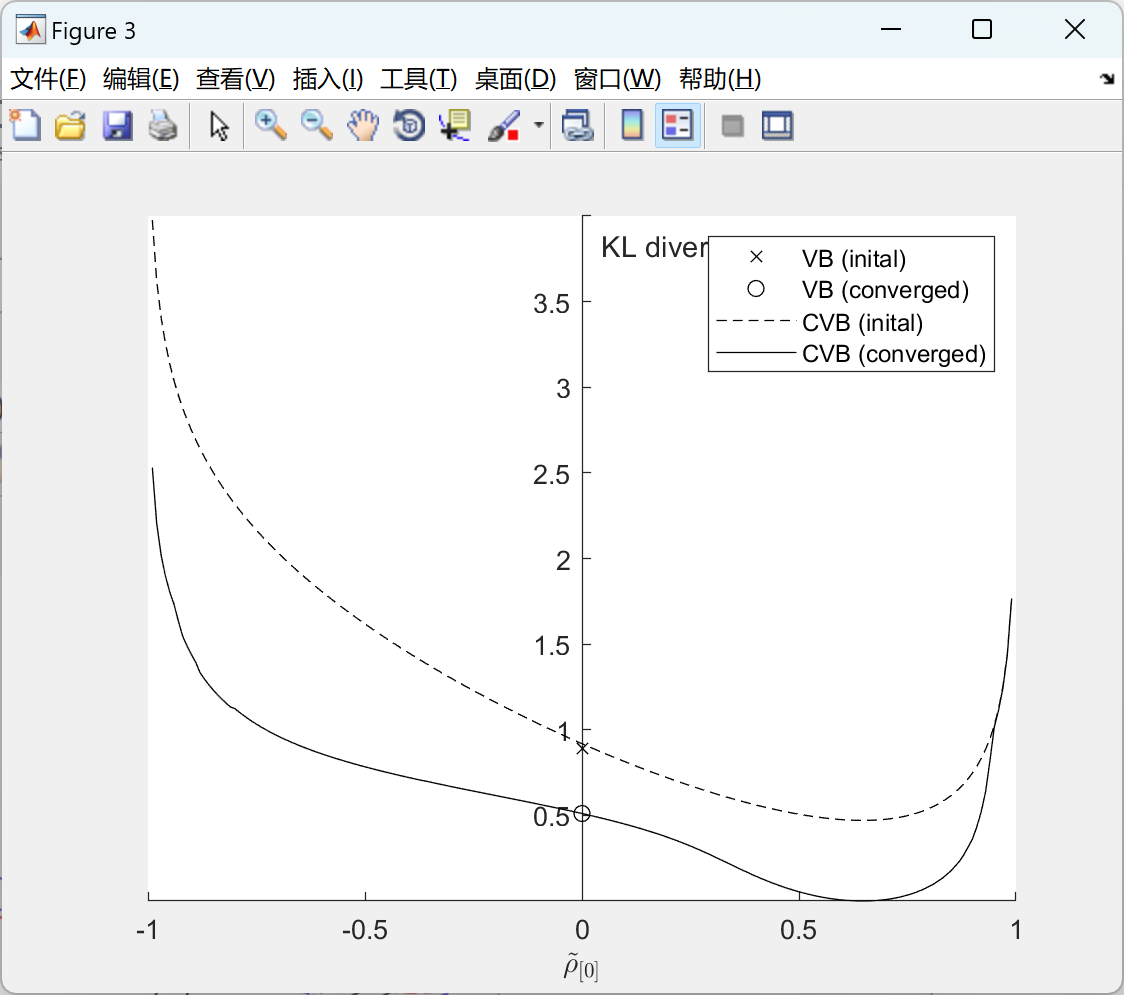
主函数部分代码：

% GAUSS (Ground truth)
GAUSS.sigmaX = 2;
GAUSS.sigmaY = 1;
GAUSS.rho = 0.8;

SIGMA.GAUSS = sigma2SIGMA(GAUSS.sigmaX,GAUSS.sigmaY,GAUSS.rho);
SIGMA.GAUSS0= sigma2SIGMA(GAUSS.sigmaX,GAUSS.sigmaY,0);

% CVB approx
nVB  = 100; %maximum number of iVB

Rho  = -0.99:0.01:0.99;

nRho = length(Rho);
%------------------------------------- declaration
CVB.sigmaX = zeros(nRho,nVB);
CVB.sigmaY = zeros(nRho,nVB);
CVB.rho    = zeros(nRho,nVB);
CVB.KLD   = zeros(nRho,nVB);

MR_KLD0 = zeros(nRho,1);
CopKLD0 = zeros(nRho,1);
MR_KLDend = zeros(nRho,1);
CopKLDend = zeros(nRho,1);

nCVB = zeros(1,nRho);
KLDend = zeros(1,nRho);
%------------------------------------- initialization
CVB.sigmaX(:,1) = 1;
CVB.sigmaY(:,1) = 1;
CVB.rho(:,1) = Rho';
%//

SIGMA.MR = sigma2SIGMA(CVB.sigmaX(1,1),CVB.sigmaY(1,1),0);
MR_KLD0(:)  = Func_KLDMultiGauss(SIGMA.MR  ,SIGMA.GAUSS0);

for iRho = 1:nRho
    
    SIGMA.CVB = sigma2SIGMA(CVB.sigmaX(1,1),CVB.sigmaY(1,1),CVB.rho(iRho,1));
    
    CVB.KLD(iRho,1)= Func_KLDMultiGauss(SIGMA.CVB ,SIGMA.GAUSS);
    CopKLD0(iRho) = CVB.KLD(iRho,1) - MR_KLD0(1);
        
for iVB = 2:2:(nVB-2) 
    
    %------------------------------------- X to Y
    
    [CVB.sigmaX(iRho,iVB)  ,CVB.sigmaY(iRho,iVB)  ,CVB.rho(iRho,iVB),CVB.KLD(iRho,iVB)] = Func_CVB_biGauss(CVB.sigmaX(iRho,iVB-1),CVB.sigmaY(iRho,iVB-1),CVB.rho(iRho,iVB-1),GAUSS.sigmaX,GAUSS.sigmaY,GAUSS.rho);

    %------------------------------------- Y to X
    
    [CVB.sigmaY(iRho,iVB+1),CVB.sigmaX(iRho,iVB+1),CVB.rho(iRho,iVB+1),CVB.KLD(iRho,iVB+1)] = Func_CVB_biGauss(CVB.sigmaY(iRho,iVB),CVB.sigmaX(iRho,iVB),CVB.rho(iRho,iVB),GAUSS.sigmaY,GAUSS.sigmaX,GAUSS.rho);
    
    if (CVB.KLD(iRho,iVB)-CVB.KLD(iRho,iVB+1)) <= (0.01 * CVB.KLD(iRho,iVB))
        nCVB(iRho) = iVB;
        KLDend(iRho) = CVB.KLD(iRho,iVB+1);
        
        SIGMA.CVB = sigma2SIGMA(CVB.sigmaX(iRho,iVB+1),CVB.sigmaY(iRho,iVB+1),CVB.rho(iRho,iVB+1));
        SIGMA.MR  = sigma2SIGMA(CVB.sigmaX(iRho,iVB+1),CVB.sigmaY(iRho,iVB+1),0);
        
        MR_KLDend(iRho) = Func_KLDMultiGauss(SIGMA.MR  ,SIGMA.GAUSS0);
        CopKLDend(iRho) = KLDend(iRho) - MR_KLDend(iRho);
        
        break;
    end
end
end
%