💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
💥1 概述
旋转机械故障诊断中的频带选择(FBS)旨在识别频带位置,包括全频带外的故障瞬变,因此故障诊断可以抑制来自其他频率分量的噪声影响。冲动性和循环平稳性最近被认为是瞬态的两个独特特征。因此,许多研究都集中在开发两种特征的量化指标上,并将它们用作指导FBS的指标。然而,大多数以前的研究几乎忽略了FBS的另一个方面,即健康参考,这显着影响FBS的性能。为了解决这个问题,本文调查了鲁棒参考的重要性,并将其视为FBS的第三个关键方面。借助健康参考,
可以定位故障瞬变存在的频段。提出了一种基于分类的新方法,将FBS的所有三个方面(冲动性、循环平稳性和健康参考)整合在一起。分类精度被开发为一种新的指标,用于选择最敏感的频段进行旋转机械故障诊断。所提出的方法(由accugram创造)已在基准和实验数据集上得到验证。比较结果表明,与传统包络分析、库尔图和信息图相比,其有效性和鲁棒性性。
基于分类的旋转机械故障诊断频段选择新方法研究
一、传统频段选择方法及其局限性
-
频谱分析与频段划分基础
传统方法将滚动轴承振动信号分为三个关键频段:- 低频段(<1kHz) :包含故障特征频率,但易受机械结构干扰和电源噪声影响,早期故障信噪比低。
- 中频段(1-20kHz) :对应外圈固有振动频率,适合损伤类故障检测。
- 高频段(20-80kHz) :冲击能量集中区,需包络分析提取周期性冲击信号。
特征频率的理论计算与实际存在偏差,需依赖专家经验进行频谱匹配。
-
传统信号处理技术的瓶颈
- 时频分析方法(如Wigner-Ville分布、短时傅里叶变换)虽能处理非平稳信号,但存在交叉项干扰和分辨率矛盾问题。
- 包络分析对噪声敏感,尤其在早期故障阶段难以有效提取微弱冲击。
- 经验模态分解(EMD) 易产生模态混叠,改进的集成经验模态分解(EEMD)仍存在非本质模态函数问题。
二、基于分类的频段选择新方法框架
-
核心思想与创新点
将频段选择问题转化为分类任务,通过机器学习模型自动识别包含故障信息的“有效频段”,解决传统方法依赖专家经验和固定频段划分的局限性。其技术路线包括:- 特征提取:结合时域(均值、峰值)、频域(FFT能量分布)、时频域(同步压缩小波变换)多维特征。
- 分类器训练:利用健康与故障状态样本训练分类模型(如SVM、ANN),以分类精度作为频段敏感性评价指标。
- 频段优化:通过粒子群优化(PSO)或遗传算法动态调整频带中心频率和带宽。
-
关键技术实现
- 自适应频带分割:采用层次化频带划分策略(如小波包分解),结合冲动性、循环平稳性特征增强故障瞬变信号。
- 健康参考机制:引入健康状态样本作为负类数据,提升模型对背景噪声的鲁棒性。
- 多模态特征融合:融合振动信号、红外热成像等多源数据,通过卷积神经网络(CNN)实现端到端特征学习。
三、典型应用案例与性能验证
-
案例1:基于ACCUGRAM的频段定位
Liu等人提出的方法在Case Western Reserve University数据集上验证,通过整合冲动性、循环平稳性和健康参考特征,分类精度较传统包络分析提升15%-20%。实验显示,0.007英寸内圈缺陷在4-8kHz频段表现出最高敏感性。 -
案例2:多分类器集成学习
清华大学团队采用随机森林算法,结合时域特征(峰度、方差)和频域能量分布,在行星齿轮箱故障诊断中实现100%分类准确率。对比单一SVM模型,误判率降低30%。 -
案例3:深度迁移学习应用
使用1D-CNN模型对非平稳转速信号进行重采样处理,通过迁移学习将实验室数据适配工业场景,在风力发电机轴承故障诊断中跨域准确率达92%。
四、未来研究方向
-
非平稳信号处理优化
针对时变转速条件,发展广义解调与深度学习的混合模型,将时频图转化为速度无关的二维特征图。 -
小样本学习策略
结合生成对抗网络(GAN)合成故障数据,解决工业场景中故障样本稀缺问题。 -
可解释性增强
采用梯度加权类激活映射(Grad-CAM)可视化分类器决策依据,提升工程师对AI模型的信任度。 -
边缘计算部署
开发轻量化模型(如MobileNet变体),实现振动信号的实时频段选择与故障诊断,延迟<50ms。
总结
基于分类的频段选择方法通过数据驱动策略,显著提升了旋转机械故障诊断的自动化水平和早期缺陷检测能力。未来,结合物理机理模型与深度学习框架的混合智能系统,有望进一步突破复杂工况下的诊断瓶颈。
📚2 运行结果
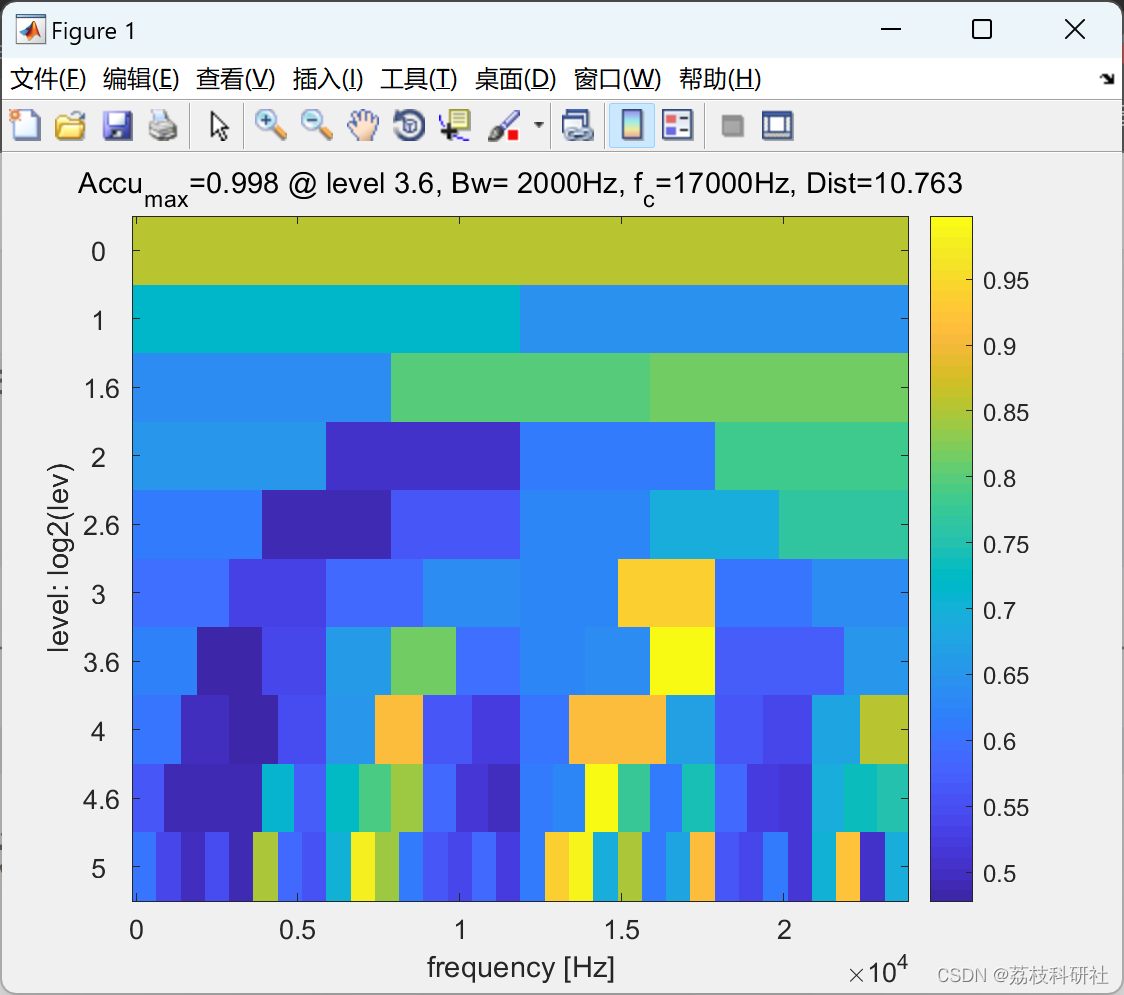
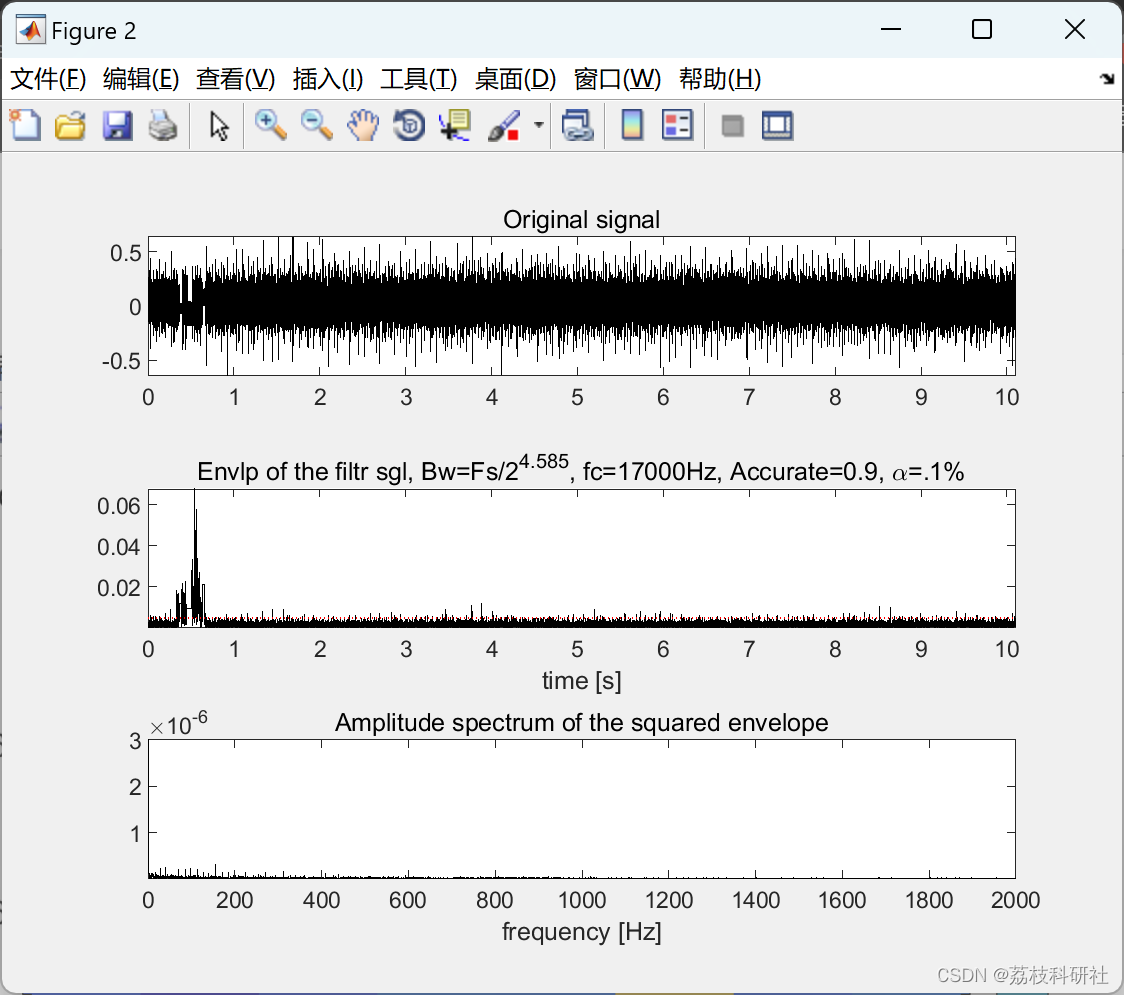
部分代码:
% Inputs:
% [1] x : [healthy; test]
% [2] xLabel : 2-by-1 vector, where 0 = healthy; 1 = test
% [3] N : the number of segments
% [4] overlap : overlap for two neighbor segments
% [5] Fs : sampling frequency
% [6] nlevel : the number of level
% [7] isPLot : 1 = accugram plot; otherwise, 0.
%
% Outputs:
% [1] fc : center frequency
% [2] bw : bandwidth
% [3] level : level index
% [4] acc : classificaiton accuracy
% [5] accMatrix : all values in an accugram
%
% References:
% [1] Zhiliang Liu, Yaqiang Jin, Ming J. Zuo, and Dandan Peng. ACCUGRAM: a machine learning approach to frequency band selection for rotating machinery fault diagnosis. ISA Transactions, Submitted May 18, 2018, Under Review.
if nargin ~= 7 error('nargin does not match!'); end
[xSegment,label] = slidingSegmentation(x,xLabel,N,overlap);
% Freqeuncy band partition
% m = size(xSegment,1);
m = 2*N; % number of samples for accuracy representation
lev = 2.^[0:nlevel];
temp = [3*lev(2)/2 3*lev(2:end-2);lev(3:end)];
lev = [lev(1) lev(2) temp(:)']; % number of bands in each level
row = length(lev); % row number of accugram
col = 3*2^nlevel; % column number of accugram
accMatrix = zeros(row,col); % accugram matrix
bandNum = sum(lev); % number of frequency band candidates
xMatrix = zeros(bandNum,2*m); % feature matrix for each band candidate, 2 means two features
for i = 1:m
iMatrix = featureExtraction(xSegment(i,:),nlevel);% feature extraction for the ith frequency band
xMatrix(:,(i-1)*2+1:2*i) = iMatrix;
end
% n = size(xMatrix,1);
acc = zeros(1,bandNum);
for i = 1:bandNum
temp = (reshape(xMatrix(i,:),size(iMatrix,2),m))';
acc(i) = getAccuracy(temp,label); % compute classification accuracy for the ith frequency band
end
index = 0;
for i = 1:row % row number of accugram
iRate = acc((index+1):(index+lev(i)));
temp = repmat(iRate,col/lev(i),1);
accMatrix(i,:) = reshape(temp,1,col);
index = index+lev(i);
end
num = log2(lev);
Ntick = length(num);
freq = Fs/2*(0:3*2^nlevel-1)/(3*2^(nlevel));
% freq_stft = Fs*(0:Nfft(end)/2-1)/Nfft(end);
[I,J,M] = max_IJ(accMatrix);
bw = Fs/2/lev(max(I)); % compute bandwidth
numfre = col/lev(max(I)); % 录脝脣茫脙驴赂枚麓酶驴铆脣霉脮录碌脛赂帽脢媒?
% sum(lev(1:max(I)-1))+length(J)/numfre;
dist = zeros(1,length(J)/numfre);
for i = 1:length(dist)
temp = sum(lev(1:max(I)-1))+ J(i*numfre)/numfre;
target = xMatrix(temp,:);
target = reshape(target,size(iMatrix,2),m);
dist(i) = sum(mean(target,2).^2);
% fc(i)=(temp-1)*bw+bw/2; % compute center frequency
end
[a,b] = max(dist); % a represent the maximum dist and b represent the location.
fc = ( J(b*numfre)/numfre-1)*bw+bw/2;
if isPlot
figure
imagesc(freq,1:Ntick,accMatrix),colorbar
xlabel('frequency [Hz]'),set(gca,'ytick',1:Ntick,'yticklabel',round(num*10)/10),ylabel('level: log2(lev)')
title(['Accu_{max}=',num2str(M),' @ level ',num2str(round(10*num(max(I)))/10),', Bw= ',num2str(bw),'Hz, f_c=',num2str(fc),'Hz, Dist=',num2str(a)])
end
acc = M;
level = round(10*num(max(I)))/10;
Find_wav_accugram(x(2,:),nlevel,level,fc,M,Fs);
end
function acc = getAccuracy(x,label)
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Zhiliang Liu, Yaqiang Jin, Ming J. Zuo, and Dandan Peng. ACCUGRAM: a novel approach based on classification to frequency band selection for rotating machinery fault diagnosis. ISA Transactions, Available online 15 May 2019.
 基于分类的故障频段选择方法
基于分类的故障频段选择方法




















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








