0/0型 ①洛必达 ②等价无穷小代换 ③泰勒公式
遇到两个根号相减→方法一:有理化 方法二:拉格朗日中值定理(两个函数值的差)
遇到tanx-sinx→想到tanx=sinx/cosx,sinx=tanx•cosx 提取出公因子→tanx-sinx=tanx(1-cosx)
遇到1-cosx→等价代换 遇到x-ln(1+x)→等价代换
遇到两个以e为底的指数函数相减→方法一:提取相同因子,变乘积,使得括号内等价代换ax+b(前提指数趋于0)。方法二:拉格朗日中值定理(看做两个函数值的差)
遇到在相减的式子中有单个的cosx→可以根据另外几个数的阶级,泰勒展开【出现函数值的差值 都可以试一下拉格朗日中值定理!】
遇到分子是arctanx-sinx→增减一项x:(arctanx-x)+(x-sinx)~【加减关系中可以用等价无穷小代换的条件:减法中两减项不等价
,a-b~a1-b1;加法中两加项
,a+b~a1+b1】
遇到积分区间为0到x的定积分→不好积时可以等价代换化简,eg.0到x的定积分fln(1+t的平方)dt~ft的平方dt=1/3x的三次方 x+sinx→等价代换2x
遇到x趋于0,(1+x)^a→等价代换ax
【推广到a(x)趋于0,a(x)b(x)趋于0,→等价代换a(x)b(x)】多用于出现幂指函数时(底数包含x,指数也包含x),把底数凑成1+a(x)的形式再用等价代换
【推广到x趋于0,→等价代换
】
同时遇到cosx,e^x,ln(1+x)→泰勒展开式
遇到x趋于0时x+ln(1-x)→=ln(1-x)-(-x)~
∞/∞型 ①洛必达 ②分子分母同除以分子和分母各项中最高阶的无穷大
【怎么找出最高阶的无穷大?】常用的一些无穷大趋向无穷的速度快慢比较:当x→+∞时,对数函数<<幂函数<<指数函数(都是比较规范的函数:对数函数的底数大于0,幂函数的幂次大于0,指数函数的底数大于1)武忠祥P12
遇到x趋于-∞时→注意无穷大趋向无穷的速度快慢比较:是当x→+∞时,所以这里特别注意,分子和分母各项中最高阶的无穷大有可能是(-x),而不是x
∞-∞型 ①分式差:通分变成0/0型 ②根式差:根式有理化 ③∞-∞型,提出无穷因子,再等价代换or变量代换(eg.令x=1/t)or泰勒公式
遇到cotx→转化成
∞-∞型,分式差:通分后遇到→
,等价代换
等价代换:x趋于0时【推广到x趋于∞时
】
【 ∞-∞型:可提出无穷因子
,再等价代换】
【遇到幂指函数,先取对数,保持恒等!】eg.
综合复杂题,用到多种方法:部分是∞/∞型→分子分母同除各项中最高阶的无穷大,整体是∞-∞型分式差→通分,出现幂指函数→取对数保持恒等,基本极限x趋向+∞时lim(1+1/x)^x=e
①前半部分是∞/∞型,先尝试化简→分子分母同除各项中最高阶的无穷大
,
②整体是∞-∞型分式差→通分,分子中提出无穷因子x
③分母中出现基本极限
,极限非零的因子的极限可以先提出
④幂指函数→取对数,保持恒等:
⑤等价代换:x趋于0时
,式中
⑥再凑出一个等价代换:x趋于0时
0×∞型 ①化成0/0型 ②化成∞/∞型
再用0/0型 ①洛必达②等价无穷小代换③泰勒公式;∞/∞型 ①洛必达②分子分母同除以分子和分母各项中最高阶的无穷大
题型:0×∞型,带绝对值求极限
【特殊的等价代换:x趋向于1时,lnx=ln[1+(x-1)]~x-1】
★0×∞型 ,化成∞/∞型【注意把复杂的对数函数ln放在分子上】,再用洛必达
遇到带绝对值的时候用洛必达→其实只需分类讨论:x<1时,[ln|1-x|]’=[ln(1-x)]’=
;当x>1时,[ln|1-x|]’=[ln(x-1)]’=
。综上可得[ln|1-x|]’=
。
 型 ①凑基本极限 ②幂指函数取对数改写成指数函数 ③利用结论
型 ①凑基本极限 ②幂指函数取对数改写成指数函数 ③利用结论
若limα(x)=0,limβ(x)=∞,且limα(x)β(x)=A,则lim=
【方法③最简单,三步走:(1)写标准型 原式=lim (2)求极限 lim
(2)求极限 lim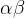 =A (3)写结果 原式=
=A (3)写结果 原式= 】
】

遇到一个复杂的幂指函数→可以拆成两个简单的幂指函数分别求极限
【选择题中出现常数a,也可以用特殊值法设a=0来化简式子】
遇到cos2x→想到化开cos2x==
 和
和 型,这类极限的函数一定是幂指函数lim
型,这类极限的函数一定是幂指函数lim![\left [ f\left ( x \right ) \right ]^{g\left ( x \right )}](https://latex.csdn.net/eq?%5Cleft%20%5B%20f%5Cleft%20%28%20x%20%5Cright%20%29%20%5Cright%20%5D%5E%7Bg%5Cleft%20%28%20x%20%5Cright%20%29%7D) ①幂指函数取对数,保持恒等lim
①幂指函数取对数,保持恒等lim 。
。
化为0·∞型 ①化成0/0型 ②化成∞/∞型
遇到求幂指函数嵌套幂指函数的极限
★先判断出极限的类型:
【幂指函数比较多也没关系,挨个取对数保持恒等即可】












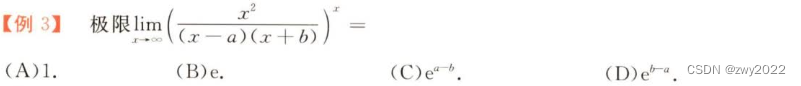
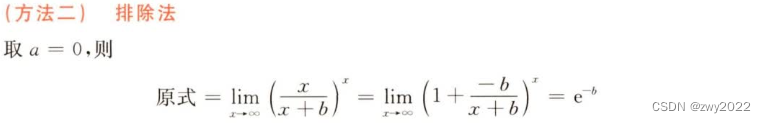



















 1941
1941

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








