任务：拟合曲面

3d

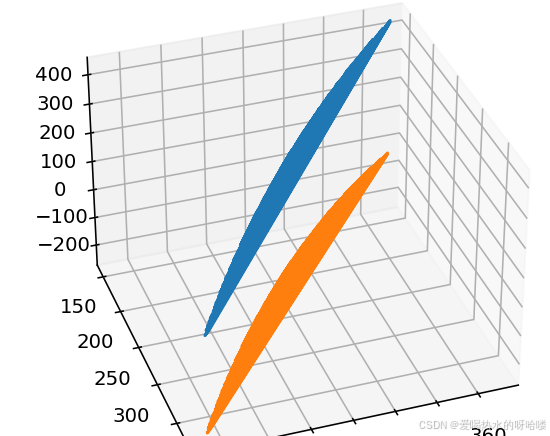
要拟合粗的蓝色曲面，剩下三条线是在3个平面的投影 

1

2

3

进度1：多项式拟合

%matplotlib notebook

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
# ax.plot(x,y,x**2+y**2)
# ax.plot(x,y,-(popt[0]*x+popt[1]*x**2+popt[2]*y+popt[3]*y**2)/popt[4])
def func(x,a,b,c,d,e,f,g,h,i):
    x1,x2,x3=x
    return a*x1++b*x1**2+c*x2+d*x2**2+e*x3+f*x3**2+g+h*x1**3+i*x2**3
a=pd.read_excel("3维有功边界点数据.xlsx")
x,y,z=a['P1'],a['P2'],a['P3']
# z=x**2+y**2
w0=np.array([0]*len(x))
input0=np.vstack((x,y,z))
popt,pcov=curve_fit(func,input0,w0)
ax.plot(x,y,z)
ax.plot(x,y,-(popt[0]*x+popt[1]*x**2+popt[2]*y+popt[3]*y**2+popt[7]*x**3+popt[8]*y**3)/popt[4]+popt[6])

 不太行，到三次都不太行、

当使用最小二乘法进行多项式拟合时，如果发现拟合结果与实际数据的差异较大（即残差大），可以尝试以下几种方法来改进：

1. 增加多项式的次数：通常情况下，提高多项式的次数可以提高模型的复杂度，从而更好地捕捉到数据的趋势。但是要注意过拟合的风险，即模型在训练集上表现很好但在测试集上表现不佳。

2. 正则化：通过引入正则化项如L1或L2正则化，可以帮助减少过拟合的风险，同时保持模型的简单性。

3. 特征选择：检查是否所有的输入变量都是必要的。有时候去除一些不相关的变量可以提高模型的性能。

4. 交叉验证：使用交叉验证来评估模型的泛化能力，而不是仅仅依赖一个固定的训练/测试划分。

5. 不同的初始条件：如果你在使用迭代算法（如梯度下降）来进行拟合，那么改变初始参数值可能会得到不同的结果。

6. 非线性变换：考虑对数据进行某种形式的非线性变换，比如对数、指数或其他函数转换，以使数据更适合线性模型。

7. 其他类型的模型：考虑使用其他的模型类型，例如支持向量机(SVM)、随机森林、神经网络等，这些模型可能更适用于某些特定类型的数据。

8. 更多的数据：如果有条件的话，收集更多的数据样本也可能有助于改善模型的准确性。

9. 可视化分析：通过绘制残差图等方式来直观地分析误差分布情况，看看是否有明显的模式或异常点。

10. 调整学习率和其他超参数：对于迭代优化算法来说，适当调整学习率和其它超参数有时也能显著影响最终结果的精度。

在实际操作中，通常会综合运用上述多种策略来逐步提升模型的性能

问题发现：f(x,y,z)=0中有z的二次项，当时想着反正算出来也是0，就放着了，加上最后z的表达式常数项放错位置了，所以一直错位。令f中z只有一次项即可。

import numpy as np
from scipy.optimize import curve_fit
import pandas as pd
import matplotlib.pyplot as plt%matplotlib notebook

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

def func(x,a,b,c,d,f,g,h,i):#func(x,a,b,c):
    x1,x2,x3=x
    return a*x1++b*x1**2+c*x2+d*x2**2+f*x3+g+h*x1**3+i*x2**3#a*x1+b*x2+c*x3#

b=pd.read_excel("3维有功边界点数据.xlsx")

x,y,z=a['P1'],a['P2'],a['P3']
w0=np.array([0]*len(x))
input0=np.vstack((x,y,z))
popt,pcov=curve_fit(func,input0,w0)
a=b[:300]
x,y,z=a['P1'],a['P2'],a['P3']
ax.scatter(x,y,z)
ax.scatter(x,y,-(popt[0]*x+popt[1]*x**2+popt[2]*y+popt[3]*y**2+popt[6]*x**3+popt[7]*y**3+popt[5])/popt[4])#-(popt[0]*x+popt[1]*y)/popt[2])

meshgrid一下hh

z（x,y）显示表达，结果更简介

import numpy as np
from scipy.optimize import curve_fit
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib notebook

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
def funcz(x,a,b,c,d,g,h,i):#func(x,a,b,c):
    x1,x2=x
    return a*x1++b*x1**2+c*x2+d*x2**2+g+h*x1**3+i*x2**3#a*x1+b*x2+c*x3#

a=pd.read_excel("3维有功边界点数据.xlsx")
# a=b[:300]
x,y,z=a['P1'],a['P2'],a['P3']
# z=x**2+y**2
# w0=np.array([0]*len(x))
input0=np.vstack((x,y))
popt,pcov=curve_fit(funcz,input0,z)

ax.scatter(x,y,z)
# a=b[:100]
# x,y,z=a['P1'],a['P2'],a['P3']

# x,y=np.meshgrid(x,y)
ax.scatter(x,y,popt[0]*x+popt[1]*x**2+popt[2]*y+popt[3]*y**2+popt[5]*x**3+popt[6]*y**3+popt[4])#-(popt[0]*x+popt[1]*y)/popt[2])
# ax.scatter(x,y,-(popt[0]*x+popt[1]*x**2+popt[2]*y+popt[3]*y**2+popt[7]*x**3+popt[8]*y**3)/popt[4]+popt[6]+350)#-(popt[0]*x+popt[1]*y)/popt[2])

4d

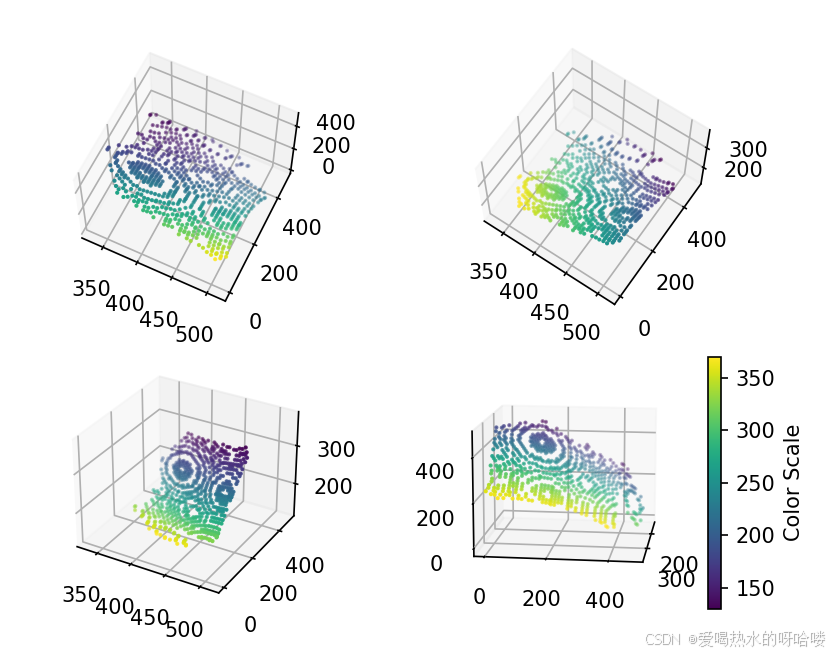
进展：感觉每三个变量单独拿出来，都能拟合成正常的曲面—— 

无语。

fig = plt.figure()
ax01 = fig.add_subplot(2, 2, 1, projection='3d')
ax02 = fig.add_subplot(2, 2, 2, projection='3d')
ax03 = fig.add_subplot(2, 2, 3, projection='3d')
ax04 = fig.add_subplot(2, 2, 4, projection='3d')
# 创建一个与散点数量相同的颜色映射值数组
colors = w  # 作为颜色映射值，但可以是任何数值数组

# 使用scatter绘制散点图，并指定颜色映射值
sc =ax01.scatter(x,y,z,s=1,c=w)#,cmap="viridis")  # 使用viridis颜色映射

# 添加颜色条
cbar = plt.colorbar(sc)  # sc是scatter返回的对象
cbar.set_label('Color Scale')  # 为颜色条设置标签

ax02.scatter(x,y,w,c=z,s=1)
ax03.scatter(x,z,w,s=1,c=y)
ax04.scatter(w,y,z,s=1,c=x)