【开黑盒系列-机器学习】核函数——原理剖析

谭贤芳

已于 2024-06-25 00:01:11 修改

阅读量819

点赞数 13

分类专栏：黑盒系列文章标签：机器学习人工智能算法

于 2024-06-24 23:22:40 首次发布

本文链接：https://blog.csdn.net/m0_70254540/article/details/139908465

版权

黑盒系列专栏收录该内容

1 篇文章 0 订阅

订阅专栏

核函数（Kernel Function）是机器学习和统计学中的一个重要概念，特别是在支持向量机（SVM）和其他基于核方法的算法中。核函数的主要作用是通过一个隐式的方式将数据映射到一个高维空间，从而使得在该高维空间中线性不可分的问题变得线性可分。

定义：

核函数 $\kappa (x, y)$ 是一个定义在输入空间中的函数，满足 $\kappa (x, y) = (\phi(x), \phi(y))$ ，其中 $\phi$ 是一个从输入空间映射到高维特征空间的映射， $<\cdot ,\cdot >$ 表示高维空间中的内积。

作用：

核函数通过计算输入数据在高维空间中对应点的内积，而不需要显式进行映射 $\phi$ 。这种方法被称为“核技巧”（Kernel Trick）。

灵魂提问：是不是在看了上面的定义后感觉云里雾里的？没关系，现在让我们抛开一切无关的事情，花20分钟来认真领会一下，核函数的原理到底是什么。

核函数为什么会诞生？

首先看一张图，这张图揭示了核函数为何诞生，它出现解决了什么样的问题。

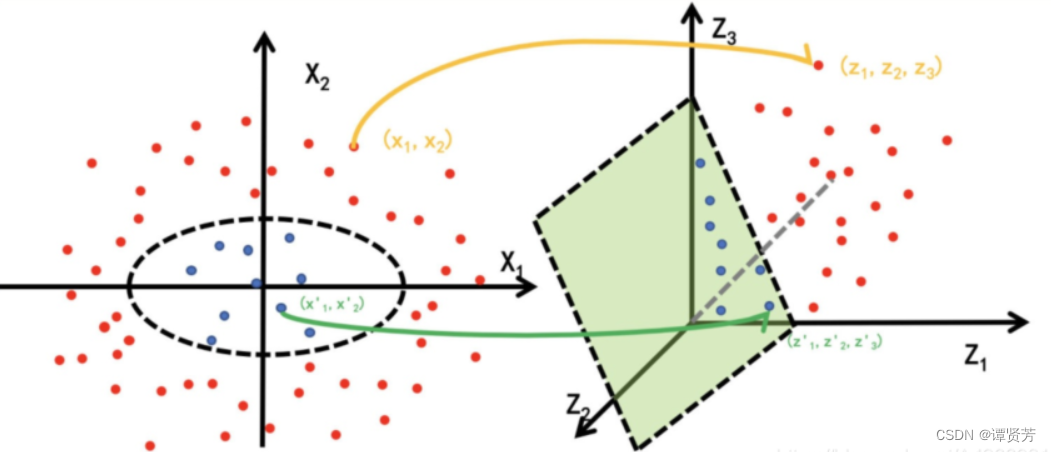
假设我们现在正在处理一个二分类问题，红蓝两类样本在原始空间 $X$ 中的分布如左图所示。如果我要将两类样本分开，在这个例子中，我需要用一个 $\frac{x_{1}^{2}}{a^2} + \frac{x_{1}^{2}}{b^2} = 1$ 的椭圆方程作为划分线进行分割。

显然这样做是比较麻烦的，对于这个例子，我们最理想的划分方式是通过一条直线就将两类样本划分开来。

但这在原始空间 $X$ 中是不可实现的，那如果我们将原始空间中的所有样本点，通过一个映射关系 $\phi$ ，从原始空间 $X$ 中“送到”右边的映射空间 $H$ 中，就可以找到一个“平面”将两类样本划分开。这个映射过程，用数学语言描述就是：

$\phi:R^2 \rightarrow R^3$

$(x_1, x_2) \mapsto (z_1, z_2, z_3) = (x_1^{2}, \sqrt{2}x_1x_2, x_2^{2})$

经过映射之后， $X$ 中的每个样本的点的坐标就由 $(x_1, x_2)$ 变为了 $(x_1^{2}, \sqrt{2}x_1x_2, x_2^{2})$ 。于是刚刚在 $X$ 空间中用于划分红蓝两类样本的椭圆方程 $\frac{x_{1}^{2}}{a^2} + \frac{x_{1}^{2}}{b^2} = 1$ 映射到 $H$ 空间中后就变成了后面这个方程 $\frac{z_1}{a^2} +0\cdot z_2 + \frac{z_3}{b^2} = 1$ 。

现在我们令原始空间中红色类别中的任意一个样本点为 $A(x_1^{}, x_2^{})$ ，任意一个蓝色类别样本点为 $B(x_1^{'}, x_2^{'})$ 。

于是在 $H$ 空间中，任意一个红色样本与任意一个蓝色样本取的内积就可以表示为：

$<\phi(x_1, x_2), \phi(x_1^{'}, x_2^{'})>$

$=<(z_1, z_2, z_3), (z_1^{'}, z_2^{'}, z_3^{'})>$

$=<(x_1^{2}, \sqrt{2}x_1x_2, x_2^2), (x_1^{'2}, \sqrt{2}x_1^{'}x_2^{'}, x_2^{'2})>$

$=x_1^2x_1^{'2} + 2x_1x_2x_1^{'}x_2^{'} + x_2^2x_2^{'2}$

$=(x_1x_1^{'} + x_2x_2^{'})^2$

这个时候你会发现，这不就是原空间 $X$ 中的内积的平方吗？于是可以再写成: $(<x, x^{'}>)^2$ 也就是说，如果想要算出高维度空间 $H$ 中 $A^{'}\cdot B^{'}$ ，其实可以先算出原始空间 $X$ 中 $A\cdot B$ 再平方。我们要找的核函数其实就是 $\kappa(x, x^{'})=$ $(<x, x^{'}>)^2$ 。

因此，我们就可以求出在 $H$ 空间中两点的之间的距离：

$\left \| \phi(x) - \phi(x^{'}) \right \|$

$=(\phi(x)-\phi(x^{'})^T)(\phi(x)-\phi(x^{'}))$

$=\phi(x)^T\phi(x)-2\phi(x)^T\phi(x^{'})+\phi(x^{'})^T\phi(x^{'})$

$= <\phi(x),\phi(x)> -2<\phi(x), \phi(x^{'})> + <\phi(x^{'},\phi(x^{'}))>$

$=\kappa(x,x)-2\kappa(x,x^{'})+\kappa(x^{'}, x^{'})$

相应的，我们也可以求出在 $H$ 空间中两向量的夹角：

$<\phi(x), \phi(x^{'})>$ $=\left \| \phi(x) \right \|\cdot \left \| \phi(x^{'}) \right \|cos\theta$

$\Rightarrow cos\theta=\frac{<\phi(x), \phi(x^{'})>}{\left \| \phi(x) \right \|\cdot \left \| \phi(x^{'}) \right \|}=\frac{<\phi(x), \phi(x^{'})>}{\sqrt{<\phi(x), \phi(x)>}\sqrt{<\phi(x^{'}), \phi(x^{'})>}}$

$=\frac{\kappa(x, x^{'})}{\sqrt{\kappa(x,x)}\sqrt{\kappa(x^{'}, x^{'})}}$

同时，我们也可以求出在 $H$ 空间中的所有点相互内积组成的 $Gram$ 矩阵，又称内积矩阵或核矩阵：

$K=\begin{bmatrix} <\phi(x_1,\phi(x_1)> & \cdots& <\phi(x_1), \phi(x_n)>& \\ \vdots& \ddots & \vdots& \\ <\phi(x_n), \phi(x_1)>&\cdots& <\phi(x_n), \phi(x_n)> & \end{bmatrix}$

$=\begin{bmatrix} \kappa(x_1,x_1)& \cdots & \kappa(x_1, x_n)\\ \vdots & \ddots & \vdots \\ \kappa(x_n,x_1)& \cdots & \kappa(x_n,x_n) \end{bmatrix}$

接下来，可以通过一个简单的例子来展示核函数 $\kappa$ 在分类上的作用。

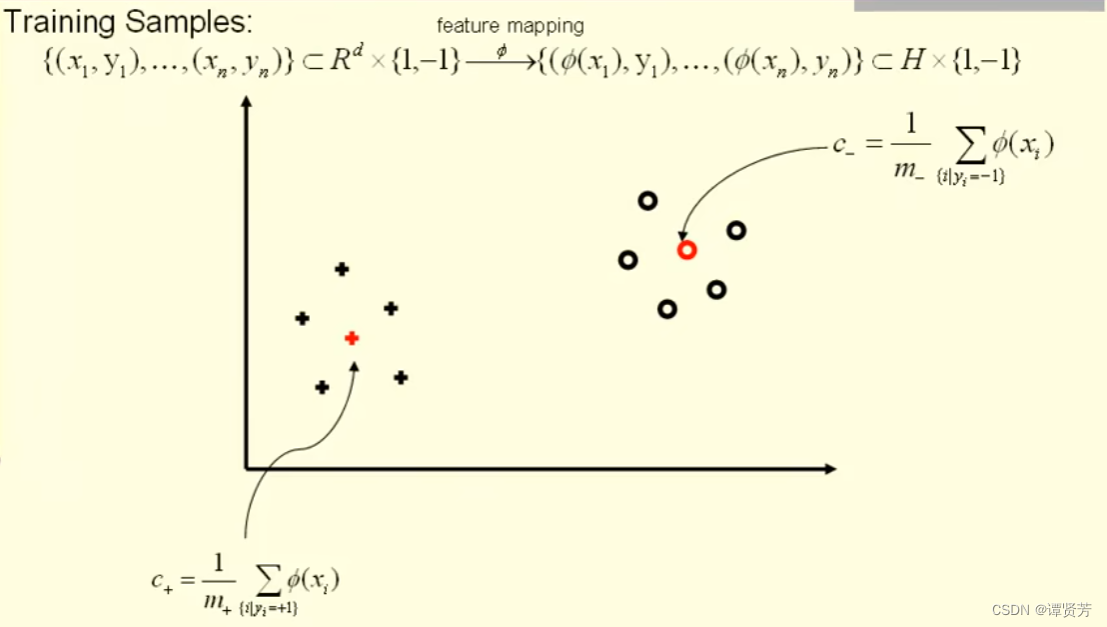
假设现在我们有训练集:

$\{(x_1,y_1),...,(x_n,y_n)\}\subset R^d \times \{1,-1\}$

这个训练集属于d维空间，每个样本可能对应的标签是-1和1。这就是一个简单的二分类问题。

现在我们通过 $\phi$ 将原始空间 $X$ 中的点送到映射空间 $H$ 中。

于是训练集就变成了:

$\{(\phi(x_1), y_1),...,(\phi(x_n),y_n)\}\subset H\times \{1,-1\}$

假设“+”标记点属于正类（y=1），“○”标记点属于负类（y=-1）。因此我们可以分别求出正负两类点的中心位置分别为：

$c_+=\frac{1}{m_+}\sum\limits_{\{i|y_i=+1\}}\phi(x_i)$ （正类中心点）

$c_-=\frac{1}{m_-}\sum\limits_{\{i|y_i=-1\}}\phi(x_i)$ （负类中心点）

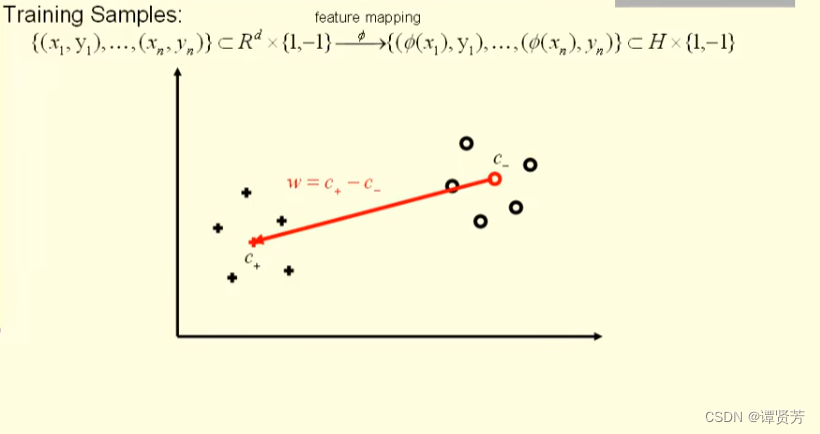
知道了中心点，根据“三角形法则”就可以求出由负类中心点指向正类中心点的红色向量为：

$w = c_+-c_-$

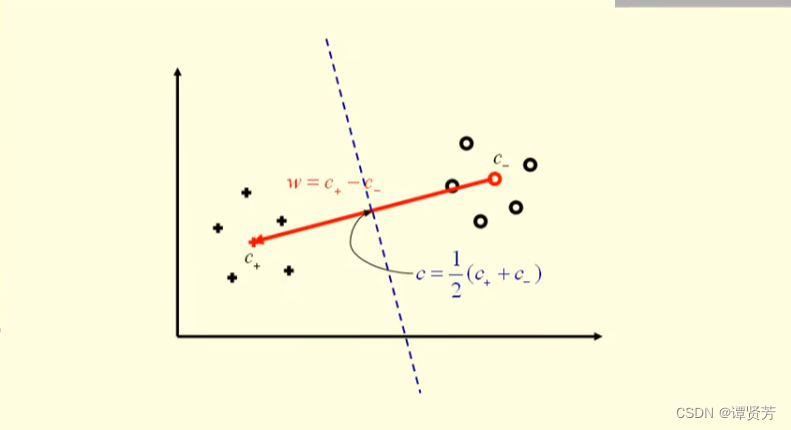
有了 $w$ 就可以在其1/2的位置做一条垂线，那现在如果有一个新的样本 $\phi(x)$ （图中绿色五角星）进来，我们该如何预测它的类别呢？

我们需要判断图中 $\theta$ 的角度大小即可。

如果是小于90度，则属于正类，即：

$y=1$

$\Leftrightarrow$ $0< cos\theta\leq 1$

$\Leftrightarrow$ $0< \frac{<\phi(x)-c,w>}{\sqrt{\left \| \phi(x)-c \right \|^2\sqrt{\left \| w \right \|^2}}}\leq 1$

$\Leftrightarrow$ $<\phi(x)-c,w>\ \ \geq 0$

如果是大于90度，则属于负类，则：

$y=-1$

$\Leftrightarrow$ $-1\leq cos\theta< 0$

$\Leftrightarrow$ $-1\leq \frac{<\phi(x)-c,w>}{\sqrt{\left \| \phi(x)-c \right \|^2\sqrt{\left \| w \right \|^2}}}< 0$

$\Leftrightarrow$ $<\phi(x)-c,w>\ \ \leq 0$

最后将 $<\phi(x)-c,w>$ 算出来的值通过信号函数 $sgn = \left\{\begin{matrix} x<0,-1\\x\geq 0 ,+1 \end{matrix}\right.$ 处理之后就可以得到类别。

到这里，很容易知道，我们只要能算出 $<\phi(x)-c,w>$ 就可以对未知样本进行分类。

于是：

$<\phi(x)-c,w>$

$=w^T(\phi(x)-c)$

$=w^T\phi(x)-w^Tc$

将 $w = c_+-c_-$ 和 $c=c_++c_-$ 带入上式

$=(c_+-c_-)^T\phi(x)-\frac{1}{2}(c_+-c_-)^T(c_++c_-)$

$=(\frac{1}{m_+}\sum\limits_{\{i|y=+1\}}\phi(x_i)-\frac{1}{m_-}\sum\limits_{\{i|y=-1\}}\phi(x_i))^T\phi(x)-(\frac{1}{2}c^T_+c_+-c_+^{T}c_-+\frac{1}{2}c_-^Tc_-)$

$=(\frac{1}{m_+}\sum\limits_{\{i|y=+1\}}\phi(x_i)^T\phi(x)-\frac{1}{m_-}\sum\limits_{\{i|y=-1\}}\phi(x_i)^T\phi(x))-b$

我们又嗅到了熟悉的味道，前面部分又可以用 $\kappa$ 来计算，于是：

$=(\frac{1}{m_+}\sum\limits_{\{i|y_i=+1\}}\kappa(x, x_1)-\frac{1}{m_-}\sum\limits_{\{i|y_i=-1\}}\kappa(x, x_1))-b$

现在，我们只需要找到核函数 $\kappa$ 就可以进行计算并进行分类。

于是又有以下的疑问：

1、 $\phi$ 是不是必须要知道？ No！

2、我们是不是只需要 $\kappa$ 就可以进行求解？ Yes！

3、那么什么样的 $\kappa$ 是符合要求的，具有什么性质？ 有限半正定的(一会讲解)

4、给定一个映射 $\phi$ ，我们能不能找到一个相关的核函数 $\kappa$ 计算 $H$ 空间中的内积? Yes!

5、给定一个核函数 $\kappa$ ，我们能不能构建一个特征空间 $H$ ？ Yes!

什么是有限正半定函数？

首先我们先了解清楚什么是半正定矩阵：

一个对称矩阵 $A\in \mathbb{R}^{n\times n}$ 被称为半定矩阵，如果对于所有非零向量 $x\in \mathbb{R}^n$ ，都有： $X^TAX\geq 0$ ,换句话说，任何向量与这个矩阵做双线性乘积的结果总是非负的。

然后我们来说什么什么样的函数有资格称为核函数，也就是上面说的一个函数的内积矩阵是半正定矩阵。

$K=\begin{bmatrix} <\phi(x_1,\phi(x_1)> & \cdots& <\phi(x_1), \phi(x_n)>& \\ \vdots& \ddots & \vdots& \\ <\phi(x_n), \phi(x_1)>&\cdots& <\phi(x_n), \phi(x_n)> & \end{bmatrix}$

$=\begin{bmatrix} \kappa(x_1,x_1)& \cdots & \kappa(x_1, x_n)\\ \vdots & \ddots & \vdots \\ \kappa(x_n,x_1)& \cdots & \kappa(x_n,x_n) \end{bmatrix}$

以下是常用的核函数: