转速闭环直流调速系统

最新推荐文章于 2025-03-11 13:11:44 发布

小z不会累～

最新推荐文章于 2025-03-11 13:11:44 发布

阅读量1.6w

点赞数 19

文章标签：自动化

本文链接：https://blog.csdn.net/m0_70748084/article/details/125485563

版权

调速范围

$D=\frac{n_{\max}}{n_{\min}}=\frac{n_Ns}{\bigtriangleup n_N\left( 1-s \right)}$

$n_{max}$ 表示同向最高转速， $n_{min}$ 表示同向最低转速。 $n_N$ 为最高转速， $\bigtriangleup n_N$ 为额定负载下的转速降落。

静差率

$s=\frac{\bigtriangleup n_N}{n_0}\times 100\%$

$\bigtriangleup n_N$ 表示转速降落， $n_0$ 表示理想空载转速，静差率是用来衡量调速系统在负载变化下转速的稳定度的。它和机械特性的硬度有关，特性越硬，静差率越小，转速的稳定度就越高。

直流电机的额定速降

$\bigtriangleup n_N=\frac{RI_N}{C_e}$

$R$ 为电枢回路电阻， $I_N$ 为额定负载电流， $C_e$ 为电动势系数

3.1 比例控制转速闭环直流调速系统

原理框图如图3-1所示

忽略各种非线性因素以及控制电源和电位器的内阻，各环节的稳态关系如下：

电压比较环节： $\bigtriangleup U_n=U_{n}^{*}-U_n$

比例调节器： $U_c=K_p\bigtriangleup U_n$

电力电子变换器： $U_{d0}=K_sU_c$

直流电动机： $n=\frac{U_{d0}-I_dR}{C_e}$

测速反馈环节： $U_n=\alpha n$

$K_p$ 为比例调节器的系数， $\alpha$ 为转速反馈系数。

转速n可由下式表示：

$n=\frac{K_pK_sU_{n}^{*}-I_dR}{C_e\left( 1+K_pK_s\alpha /C_e \right)}=\frac{K_pK_sU_{n}^{*}}{C_e\left( 1+K \right)}-\frac{RI_d}{C_e\left( 1+K \right)}$

K为闭环系统的开环放大系数， $K=\frac{K_pK_s\alpha}{C_e}$

如果断开上图中的反馈回路即为开环系统，则该系统的开环机械特性为：

$n=\frac{U_{d0}-I_dR}{C_e}=\frac{K_pK_sU_{n}^{*}}{C_e}-\frac{RI_d}{C_e}=n_{0op}-\varDelta n_{op}$

$n_{0op}$ 为开环系统的理想空载转速； $\varDelta n_{op}$ 为开环系统的稳态速降;

闭环时的静特性可写成：

$n=\frac{U_{d0}-I_dR}{C_e\left( 1+K \right)}=\frac{K_pK_sU_{n}^{*}}{C_e\left( 1+K \right)}-\frac{RI_d}{C_e\left( 1+K \right)}=n_{0cl}-\varDelta n_{cl}$

$n_{0cl}$ 为开环系统的理想空载转速； $\varDelta n_{cl}$ 为开环系统的稳态速降;

在同样的负载扰动下，开环系统和闭环系统的转速降落分别为：

$\varDelta n_{op}=\frac{RI_d}{C_e},\varDelta n_{cl}=\frac{RI_d}{C_e\left( 1+K \right)}$

它们的关系是:

$\varDelta n_{cl}=\frac{\varDelta n_{op}}{1+K}$

显然当K值较大时， $\varDelta n_{cl}$ 比 $\varDelta n_{op}$ 小得多，即闭环系统的特性要硬得多。

闭环系统和开环系统静差率的比较

$s_{cl}=\frac{\varDelta n_{cl}}{n_{0cl}},s_{op}=\frac{\varDelta n_{op}}{n_{0op}}$

按理想空载转速相同的情况比较，当 $n_{0op}=n_{ocl}$ 时，

$s_{cl}=\frac{s_{op}}{1+K}$

当静差率一定时，闭环系统可以大大提高调速范围

如果要求电动机的最高转速都是 $n_N$ ，而对最低静差率的要求相同，

开环时，

$D_{op}=\frac{n_Ns}{\varDelta n_{op}\left( 1-s \right)}$

闭环时，

$D_{cl}=\frac{n_Ns}{\varDelta n_{cl}\left( 1-s \right)}$

考虑静差率的关系可得：

$D_{cl}=\left( 1+K \right) D_{op}$

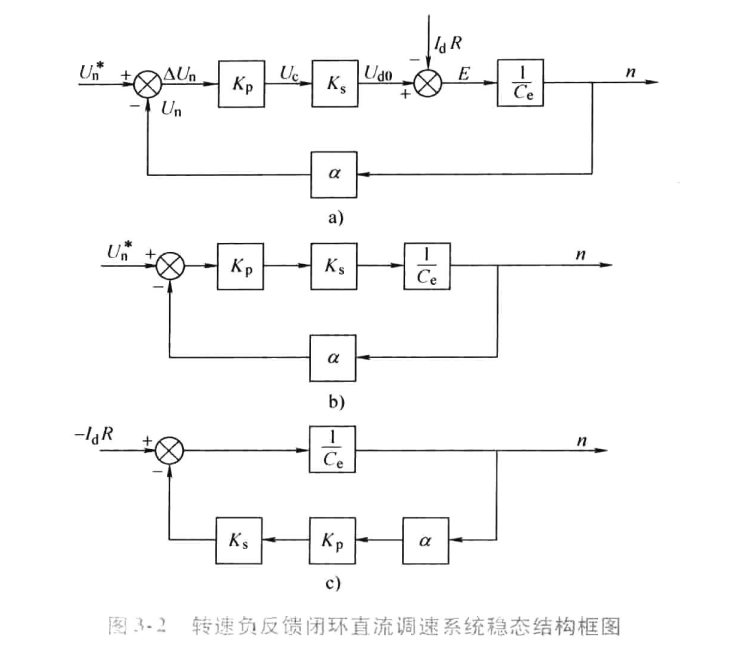
根据图3-2，系统的控制电压 $U_c$ 可表示为：

$U_c=\frac{K_pU_{n}^{*}}{1+K}+\frac{K_P\alpha RI_{dL}}{C_e\left( 1+K \right)}$

结论：

在闭环系统中，每增加(或减少)负载，相应得 $I_{dL}$ 升高(或降低),则控制电压 $U_c$ 提高(或降低)，即它能随着负载的变化而相应地改变电枢电压，以补偿电枢回路电阻压降的变化。系统稳态时控制电压由系统给定和负载共同决定。

比例控制的直流调速系统可以获得比开环调速系统硬的多的稳态特性，从而在保证一定静差率的要求下，能够提高调速范围。

闭环直流调速系统的反馈控制规律

(1)只有比例控制的反馈调速系统，其被调量有静差

我们可以通过调节比例系数 $k_p$ 来使稳态压降趋近于0，但只有当 $K\rightarrow \infty$ 时达到消除稳态误差的效果，但这在实际系统中显然是不可能实现的，并且控制器的输出 $U_c$ 与偏差成比例关系，若偏差为0此时系统控制输入也为0，所以比例反馈控制只能减小稳态误差，而不能消除它，因此这样的控制系统叫做有静差控制系统。

(2)反馈控制系统的作用是抵抗扰动，服从给定

反馈控制系统具有良好的抗扰性能，它能有效地抑制一切被负反馈环所包围的前向通道上的扰动作用，但对于反馈通道上的扰动无能为力，如果在反馈通道上的测速系数\alpha受到某种影响而发生变化，它非但不能得到反馈控制系统的抑制，反而会造成被调量的误差。

(3)系统的精度依赖于给定和反馈检测的精度

反馈通道上的扰动是比例反馈控制无法克服的，所以反馈检测装置的精度时保证控制系统精度的重要因素。如：测速发电机励磁发生变化时，会使检测到的转速反馈信号偏离应有的数值，而测速发电机电压中的换相纹波、制造或安装不良造成转子的偏心等，都会给系统带来周期性的干扰。

稳定性分析

动态电压方程为：

$U_{d0}=RI_d+L\frac{dI_d}{dt}+E$

忽略粘性摩擦及弹性力矩，电机轴上的动力学方程为：

$T_e-T_L=\frac{GD^2}{375}\frac{dn}{dt}$

额定励磁下的感应电动势和电磁转矩分别为：

$E=C_en,T_e=C_mI_d$

$T_L$ 为包括电动机空载转矩在内的负载转矩(N·m)

$GD^2$ 为电力拖动装置折算到电机轴上的飞轮惯量( $N\cdot m^2$ )

$C_m$ 为电动机额定励磁下的转矩系数(N·m/A), $C_m=\frac{30}{\pi}C_e$

定义电枢回路电磁时间常数(s) $T_l$ ,电力拖动系统机电时间常数(s) $T_m$

$T_l=\frac{L}{R}$

$T_m=\frac{GD^2R}{375C_eC_m}$

将时间常数代入上式得:

$U_{d0}-E=R\left( I_d+T_l\frac{dI_d}{dt} \right)$

$I_d-I_{dL}=\frac{T_m}{R}\frac{dE}{dt}$

$I_{dL}$ 为负载电流， $I_{dL}=\frac{T_L}{C_m}$ .

在零初始条件下，取等式两侧的拉普拉斯变换，得电压与电流间的传递函数

$\frac{I_d\left( s \right)}{U_{d0}\left( s \right) -E\left( s \right)}=\frac{1/R}{T_ls+1}$

电流与电动势间的传递函数

$\frac{E\left( s \right)}{I_d\left( s \right) -I_{dL}\left( s \right)}=\frac{R}{T_ms}$

根据上述两式画出额定励磁下直流电动机的动态结构图，

根据闭环传递函数，即省去电流 $I_d$ ，画出系统的等效框图

根据比例放大器特性和反馈测速元件特性，以及各环节的传递函数，画出闭环直流调速系统的动态结构框图

上面讨论了比例闭环反馈系统，虽然可以有效补偿加大负载带来的转速降落，但是系统仍然存在静差，所以后续通过积分器有效解决这个问题，由此引出了比例积分(PI)控制器。

3.2 无静差的转速闭环调速系统

积分调节器的作用是输出量为输入量的积分。当输入量为转速误差信号\varDelta U_n时，积分调节器的输入输出关系为

$U_c=\frac{1}{\tau}\int\limits_0^t{\varDelta U_ndt}$

其传递函数为

$W_I\left( s \right) =\frac{1}{\tau s}$

其中 $\tau$ 为积分时间常数

比例调节器的输出只取决于输入偏差量的现状，而积分调节器的输出则包含了输入偏差量的全部历史。虽然到稳态时 $\varDelta U_n=0$ ,只要历史上有过 $\varDelta U_n$ ，其积分就有一定数值，足以产生稳态运行所需要的控制电压 $U_c$ 。这就是积分控制规律和比例控制规律的根本区别。