一、线性规划(Linear Programming,简称LP)是运筹学中的一个重要分支,也是一门实用性很强的应用数学学科。它主要研究在线性约束条件下,如何优化(最大化或最小化)线性目标函数的问题。
%%线性规划求最小值
%[x,fval] = linprog(c,A,b,Aeq,beq,lb,ub,x0)
format long g %长数字格式
c = [1,1]';
A = [1,2];
b = 8;
Aeq = [1,1];
beq = 10;
lb = [0,0]';
[x,fval] = linprog(c,A,b,Aeq,beq,lb,[],[])
可以看出该方程无最优解 。
二、非线性规划(Nonlinear Programming,简称NP)是一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。它研究一个n元实函数在一组等式或不等式的约束条件下的极值问题,且目标函数和约束条件至少有一个是未知量的非线性函数。由于非线性规划问题多是NP难问题,并不容易得到最优的可行解。因此,在求解非线性规划问题时,往往需要结合近似算法、启发式算法,甚至利用强化学习等方式,以在短时间内给出一个较好的可行解。
非线性规划的基本概念包括全局最优解和局部最优解。全局最优解是指在所有可行解中,使得目标函数达到最优(最大或最小)的解;而局部最优解则是指在某个特定区域内的最优解。
此外,凸规划是非线性规划中的一个特殊类型,其特点是如果目标函数和约束函数都是凸函数,那么该问题可以求得全局最优解。
%%非线性规划求最小值
%[x,fval] = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)
%@fun目标函数,@nonlfun:[非线性不等式,非线性等式]非线性约束
clear;clc;
format long g
A = [-2,3];
b = 6;
x0 = [0,0]';
op = {'interior-point',...
'sqp','active-set'};
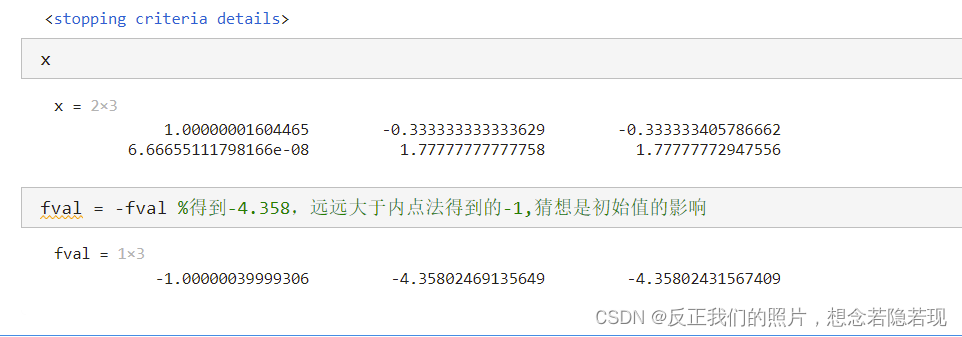
x = zeros(2,3);
fval = zeros(1,3);
for i = 1:3
option = optimoptions("fmincon",'Algorithm',op{i});
%%option有以下方法:
%interior-point——内点法
%trust-region-reflective——信赖域反射算法
%sqp——序列二次规划法
%active-set——有效集法
[x(:,i),fval(:,i)] = fmincon(@fun,x0,A,b,[],[],[],[],@nonlfun,option);
end
三、整数规划(Integer Programming)是数学规划的一个分支,其特点是规划中的变量(部分或全部)被限制为整数。在线性规划模型中,如果变量限制为整数,则称为整数线性规划。
整数规划可以分为几种不同的类型,包括纯整数规划、混合整数规划、纯0-1整数规划和混合0-1规划。在纯整数规划中,所有决策变量都必须是整数;而在混合整数规划中,只有部分决策变量需要是整数。纯0-1整数规划和混合0-1规划则是要求决策变量只能取0或1的特殊类型。
整数规划问题的求解方法有多种,包括分枝定界法、割平面法、隐枚举法等。这些方法根据问题的具体特点选择使用,以有效地找到整数规划问题的最优解。
需要注意的是,整数规划问题的最优解并不能简单地通过对实数最优解取整获得。在某些情况下,整数规划问题的最优解可能不存在,或者即使存在,其最优值也可能比实数最优解要差。
%%整数规划求最小值
%[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub,x0)
c=[18,23,5]';
intcon=3; % x3限定为整数
A=[107,500,0;
72,121,65;
-107,-500,0;
-72,-121,-65];
b=[50000;2250;-500;-2000];
lb=zeros(3,1);
[x,fval]=intlinprog(c,intcon,A,b,[],[],lb,[],[])
四、最大最小化模型是一种在决策论和运筹学中常见的优化模型。该模型主要解决的是在不利的条件下寻求最有利的策略的问题。在实际问题中,经常需要求解的是最大值的最小化问题,例如急救中心选址问题、投资规划中的风险最小化问题等。
在最大最小化模型中,对于每个可能的决策变量x(通常是一个向量),我们需要先计算目标函数f(x)的最大值。这里的f(x)可以是一个向量函数,包含多个目标函数值。然后,从这些最大值中找出最小的那个,即求解min{max[f1,f2,...,fm]}。这个最小值就是最大最小化模型的最优解。
%%最大最小化模型 min(max{f1,f2,...,fn})
%[x,fval] = fminimax(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)
x0 = [6, 6]; % 给定初始值
lb = [3, 4]; % 决策变量的下界
ub = [8, 10]; % 决策变量的上界
[x,feval] = fminimax(@Fun,x0,[],[],[],[],lb,ub,[],[])
function f = Fun(x)
a=[1 4 3 5 9 12 6 20 17 8];
b=[2 10 8 18 1 4 5 10 8 9];
% 函数向量
f=zeros(10,1);
for i = 1:10
f(i) = abs(x(1)-a(i))+abs(x(2)-b(i));
end
% f(1) = abs(x(1)-a(1))+abs(x(2)-b(1));
% f(2) = abs(x(1)-a(2))+abs(x(2)-b(2));
% f(3) = abs(x(1)-a(3))+abs(x(2)-b(3));
% f(4) = abs(x(1)-a(4))+abs(x(2)-b(4));
% f(5) = abs(x(1)-a(5))+abs(x(2)-b(5));
% f(6) = abs(x(1)-a(6))+abs(x(2)-b(6));
% f(7) = abs(x(1)-a(7))+abs(x(2)-b(7));
% f(8) = abs(x(1)-a(8))+abs(x(2)-b(8));
% f(9) = abs(x(1)-a(9))+abs(x(2)-b(9));
% f(10) = abs(x(1)-a(10))+abs(x(2)-b(10));
end 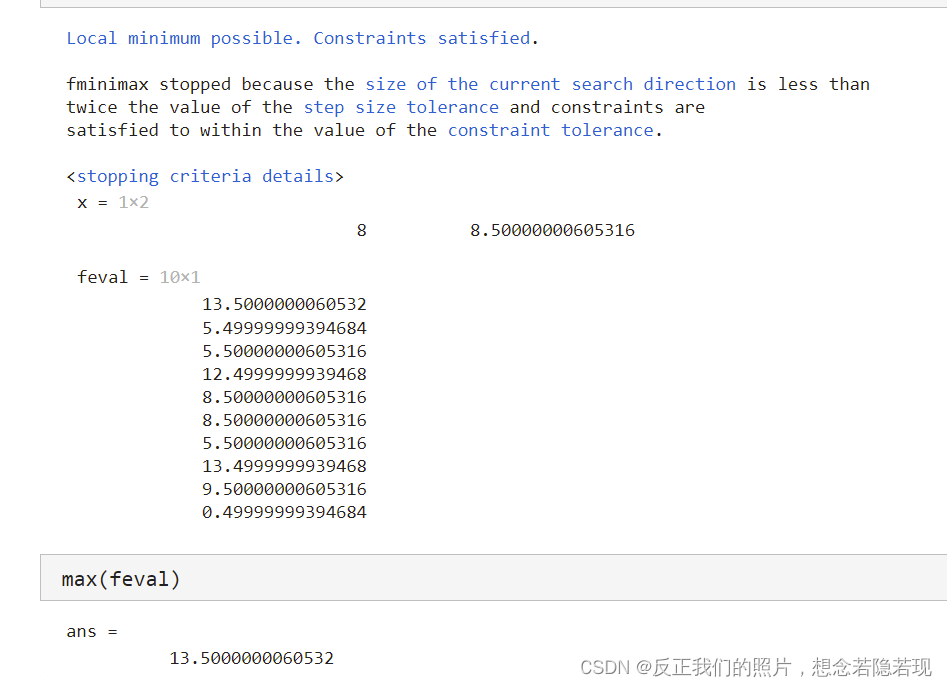







 本文探讨了线性规划、非线性规划、整数规划以及最大最小化模型在数学优化中的应用,涉及问题的定义、求解策略和特性,强调了非线性和整数问题的复杂性以及寻找最优解的挑战。
本文探讨了线性规划、非线性规划、整数规划以及最大最小化模型在数学优化中的应用,涉及问题的定义、求解策略和特性,强调了非线性和整数问题的复杂性以及寻找最优解的挑战。














 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








