非有理 B 样条曲线插值方法——给定点数据的全局曲线插值（参数化插值方法）

一、B 样条基函数的定义和性质

1.1、B 样条基函数的定义

令 U = { u 0 , u 1 , ⋯   , u m } U=\{u_0,u_1,\cdots,u_m\} U={u0​,u1​,⋯,um​} 是一个单调不减的实数序列，即 $u_i\le u_{i+1},i=0,1,\cdots ,m-1$。其中，$u_i$ 称为节点，$U$ 称为节点矢量，用 $N_{i,p}(u)$ 表示第 $i$ 个 $p$ 次（$p+1$ 阶）B 样条基函数，其定义为（也称为 Cox-deBoor 公式）
$$\begin{array}{rl}{N}_{i,0}(u)& =\{\begin{array}{ll}1,& u_i\le u<u_{i+1},\\ 0,& else\end{array}\\ N_{i,p}(u)& =\frac{u-u_i}{u_{i+p}-u_i}{N}_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}{N}_{i+1,p-1}(u)\end{array}\text{\hspace{1em}(1)}$$

由上述定义式可知：

1. 事先指定节点矢量 $U$ 和次数 $p$， 即可计算出对应的一组基函数；
2. 半开区间 $u\in [u_i,u_{i+1})$ 称为第 $i$ 个节点区间，它的长度可以为零，因为相邻节点可以是相同的；
3. 计算 $p$ 次基函数的过程生成一个如下形式的三角形阵列：（通常将 $N_{i,p}(u)$ 写为 $N_{i,p}$）
   $$\begin{gathered} N_{0,0} \\ {N}_{0,1} \\ {N}_{1,0}{N}_{0,2} \\ {N}_{1,1}{N}_{0,3} \\ {N}_{2,0}{N}_{1,2} \\ {N}_{2,1}{N}_{1,3} \\ {N}_{3,0}{N}_{2,2}⋮ \\ {N}_{3,1}⋮ \\ {N}_{4,0}⋮ \end{gathered}$$

例1. 令 U = { u 0 = 0 , u 1 = 0 , u 2 = 0 , u 3 = 1 , u 4 = 1 , u 5 = 1 } , p = 2 U=\{u_0=0,u_1=0,u_2=0,u_3=1,u_4=1,u_5=1\},p=2 U={u0​=0,u1​=0,u2​=0,u3​=1,u4​=1,u5​=1},p=2，我们分别计算 0 次、1 次和 2 次的 B 样条基函数。
$$\begin{array}{rl}& N_{0,0}=N_{1,0}=0,-\infty <u<\infty \\ & N_{2,0}=\{\begin{array}{ll}1,& 0\le u<1\\ 0,& 其他\end{array}\\ & N_{3,0}=N_{4,0}=0,-\infty <u<\infty \\ & N_{0,1}=\frac{u-0}{0-0}{N}_{0,0}+\frac{0-u}{0-0}{N}_{1,0}=0,-\infty <u<\infty \\ & N_{1,1}=\frac{u-0}{0-0}{N}_{1,0}+\frac{1-u}{1-0}{N}_{2,0}=\{\begin{array}{ll}1-u,& 0\le u<1\\ 0,& 其他\end{array}\\ & N_{2,1}=\frac{u-0}{1-0}{N}_{2,0}+\frac{1-u}{1-1}{N}_{3,0}=\{\begin{array}{ll}u,& 0\le u<1\\ 0,& 其他\end{array}\\ & N_{3,1}=\frac{u-1}{1-1}{N}_{3,0}+\frac{1-u}{1-1}{N}_{4,0}=0,-\infty <u<\infty \\ & N_{0,2}=\frac{u-0}{0-0}{N}_{0,1}+\frac{1-u}{1-0}{N}_{1,1}=\{\begin{array}{ll}(1-u{)}^2,& 0\le u<1\\ 0,& 其他\end{array}\\ & N_{1,2}=\frac{u-0}{1-0}{N}_{1,1}+\frac{1-u}{1-0}{N}_{2,1}=\{\begin{array}{ll}2u(1-u),& 0\le u<1\\ 0,& 其他\end{array}\\ & N_{2,2}=\frac{u-0}{1-0}{N}_{2,1}+\frac{1-u}{1-1}{N}_{3,1}=\{\begin{array}{ll}{u}^2,& 0\le u<1\\ 0,& 其他\end{array}\end{array}$$

1.2、B 样条基函数的性质

P1 局部支撑性

如何 $u\notin [u_i,u_{i+p+1}]$，则 $N_{i,p}(u)=0$，如下图所示，$N_{1,3}$ 是 $N_{1,0},N_{2,0},N_{3,0}$ 和 $N_{4,0}$ 的线性组合，因此 $N_{1,3}$ 仅在 $u\in [u_1,u_5)$ 上非零。

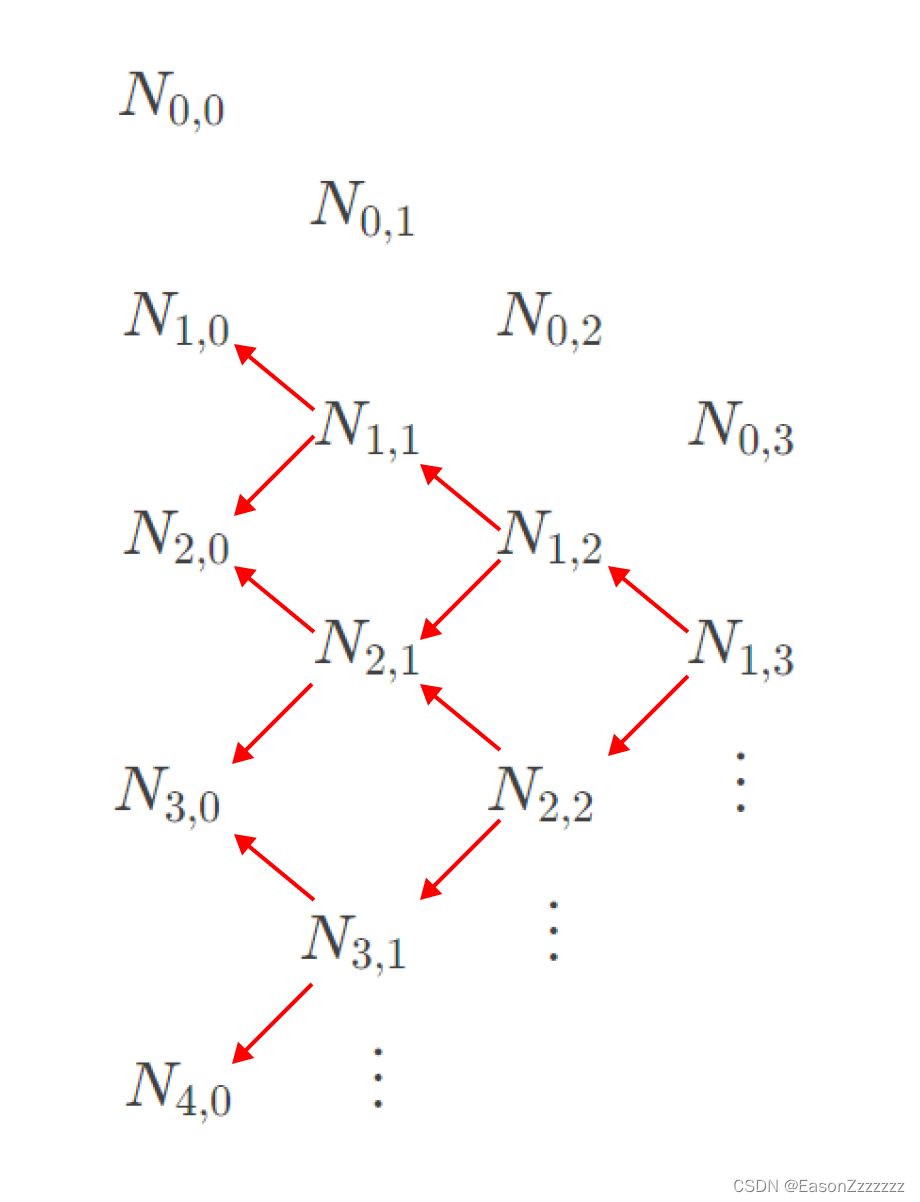
P2

在任意给定的节点区间 $[u_i,u_j)$ 内，最多 $p+1$ 个 $N_{i,p}$ 是非零的，它们是 $N_{i-p},\cdots ,N_{i,p}$。

P3 非负性

对于所有 $i,p$ 和 $u$，有 $N_{i,p}(u)\ge 0$

P4 规范性

对于任意的节点区间 $[u_i,u_{i+1})$，当 $u\in [u_i,u_{i+1})$ 时，${\sum }_{j=i-p}^i{N}_{j,p}=1$，即同一次数的基函数和为 1。

P5 可微性

在节点区间内部，$N_{i,p}(u)$ 是无限次可微的（在每个节点区间内部，它是一个多项式）。在节点处 $N_{i,p}(u)$ 是 $p-k$ 次连续可微的，其中 $k$ 是节点的重复度。因此，增加次数将提高曲线的连续性，而增加节点的重复度则使连续性降低。

P6

非周期节点矢量具有如下形式：
U = { a , ⋯   , a ⏟ p + 1 , u p + 1 , ⋯   , u m − p − 1 , b , ⋯   , b ⏟ p + 1 } (2) U=\{\underbrace{a,\cdots,a}_{p+1},u_{p+1},\cdots,u_{m-p-1},\underbrace{b,\cdots,b}_{p+1}\}\tag{2} U={p+1 a,⋯,a​​,up+1​,⋯,um−p−1​,p+1 b,⋯,b​​}(2)
定义在非周期节点矢量上，设节点个数是 $m+1$，则存在 $n+1$ 个基函数（每个控制点对应一个基函数），这里 $n=m-p-1$；并且，$N_{0,p}(a)=1，N_{n,p}(b)=1$，$N_{i,p}(a)=0,i\ne 0$ 且 $N_{i,p}(b)=0,i\ne n$

二、B 样条基函数的计算

令 U = { u 0 , u 1 , ⋯   , u m } U=\{u_0,u_1,\cdots,u_m\} U={u0​,u1​,⋯,um​} 为形如（2）式的节点矢量，假设我们感兴趣的是 $p$ 次基函数，并假设 $u$ 是固定的，$u\in [u_i,u_{i+1})$。我们给出以下两个算法，分别用来计算：

• 计算 $u$ 所属的节点区间的下标 $i$；
• 基于（1）式计算 $N_{i-p,p},\cdots ,N_{i,p}$；

由性质 P2 和假设 $u\in [u_i,u_{i+1})$，我们可以只把注意力集中在计算函数 $N_{i-p,p},\cdots ,N_{i,p}$ 上，因为其他所有函数都为 0，没必要费力去计算它们。因此，计算的第一步就是确定 $u$ 所属的节点区间，这可以对节点矢量使用二分法搜索得到。由于我们使用的区间形式为 $u\in [u_i,u_{i+1})$，在计算基函数时需要特殊考虑的一个情况是 $u=u_m$ 的情形。这时，我们直接将节点区间的下标设置为 $n=m-p-1$

def FindSpan(p, u, U):
    """
    确定参数 u 所在的节点区间的下标
    :param p: 基函数次数
    :param u: 固定点
    :param U: 节点矢量
    :return: u 所属的节点区间的下标
    """
    m = len(U) - 1
    start, end = p, m
    if u == U[-1]:
        return m - p - 1
    while end != start + 1 and end != start:
        mid_index = (start + end) // 2
        if U[mid_index] == u:
            return mid_index
        if u > U[mid_index]:
            start = mid_index
        else:
            end = mid_index
    return start

现在我们来考虑第二个算法。假设 $u$ 在第 $i$ 个节点区间内，计算所有非零 B 样条基函数的过程可形成如下的一个倒置的三角形：

我们利用（1）式写出二次基函数的一般形式，有
$$\begin{array}{rl}& N_{i-2,2}(u)=\frac{u-u_{i-2}}{u_i-u_{i-2}}{N}_{i-2,1}(u)+\frac{u_{i+1}-u}{u_{i+1}-u_{i-1}}{N}_{i-1,1}(u)\\ & N_{i-1,2}(u)=\frac{u-u_{i-1}}{u_{i+1}-u_{i-1}}{N}_{i-1,1}(u)+\frac{u_{i+2}-u}{u_{i+2}-u_i}{N}_{i,1}(u)\\ & N_{i,2}(u)=\frac{u-u_i}{u_{i+2}-u_i}{N}_{i,1}(u)+\frac{u_{i+3}-u}{u_{i+3}-u_{i+1}}{N}_{i+1,1}(u)\end{array}\text{\hspace{1em}(3)}$$

我们引入符号
$$\mathrm{left}[j]=u-u_{i+1-j}，\mathrm{right}[j]=u_{i+j}-u$$

那么（3）式可以写为
$$\begin{array}{rl}& N_{i-2,2}(u)=\frac{\mathrm{left}[3]}{\mathrm{right}[0]+\mathrm{left}[3]}{N}_{i-2,1}(u)+\frac{\mathrm{right}[1]}{\mathrm{right}[1]+\mathrm{left}[2]}{N}_{i-1,1}(u)\\ & N_{i-1,2}(u)=\frac{\mathrm{left}[2]}{\mathrm{right}[1]+\mathrm{left}[2]}{N}_{i-1,1}(u)+\frac{\mathrm{right}[2]}{\mathrm{right}[2]+\mathrm{left}[1]}{N}_{i,1}(u)\\ & N_{i,2}(u)=\frac{\mathrm{left}[1]}{\mathrm{right}[2]+\mathrm{left}[1]}{N}_{i,1}(u)+\frac{\mathrm{right}[3]}{\mathrm{right}[3]+\mathrm{left}[0]}{N}_{i+1,1}(u)\end{array}$$

基于以上观察设计算法，用来计算所有非零 B 样条基函数。

def BaseFunction(p, u, U):
    """
    计算所有非零 B 样条基函数的值
    :param u: 固定值
    :param p: 基函数次数
    :param U: 节点矢量
    :return: 基函数值数组
    """
    i = FindSpan(p, u, U)
    N = np.zeros(p + 1)
    N[0] = 1.0
    left = np.zeros(p + 1)
    right = np.zeros(p + 1)
    for j in range(1, p + 1):
        left[j] = u - U[i + 1 - j]
        right[j] = U[i + j] - u
        saved = 0.0
        for r in range(j):
            if (right[r + 1] + left[j - r]) == 0:
                temp = 0.0
            else:
                temp = N[r] / (right[r + 1] + left[j - r])
            N[r] = saved + right[r + 1] * temp
            saved = left[j - r] * temp
        N[j] = saved
    return N

三、B 样条曲线的定义和性质

$p$ 次 B 样条曲线的定义为
$$C(u)=\sum _{i=0}^n{N}_{i,p}(u)P_i,a\le u\le b\text{\hspace{1em}(1)}$$

这里 $P_i$ 是曲线的控制点， { N i , p ( u ) } \{N_{i,p}(u)\} {Ni,p​(u)} 是定义在非周期（并且非均匀）节点矢量
$$U=(\underset{p+1}{\underbrace{a,\cdots ,a}},u_{p+1},\cdots ,u_{m-p-1},\underset{p+1}{\underbrace{b,\cdots ,b}})$$

（包含 $m+1$ 个节点）上的 $p$ 次 B 样条基函数。除非特别声明，通常取 $a=0,b=1$。由 $P_i$ 构成的多边形称为控制多边形。

对于固定的 $u$ 值，计算 B 样条曲线上的对应点需要三步：

1. 找到 $u$ 所在的节点区间；
2. 计算非零的基函数；
3. 将非零基函数的值与相应的控制点相乘，再求和。

例. U = { 0 , 0 , 0 , 1 , 2 , 3 , 4 , 4 , 5 , 5 , 5 } ,    u = 5 2 ,    p = 2 \quad U=\{0,0,0,1,2,3,4,4,5,5,5\},\ \ u=\dfrac{5}{2},\ \ p=2 U={0,0,0,1,2,3,4,4,5,5,5},  u=25​,  p=2
此时，$u\in [u_4,u_5)$，则
$$N_{2,2}\left(\frac{5}{2}\right)=\frac{1}{8},N_{3,2}\left(\frac{5}{2}\right)=\frac{6}{8},N_{4,2}\left(\frac{5}{2}\right)=\frac{1}{8}$$

与相应的控制点相乘并求和得
$$C\left(\frac{5}{2}\right)=\frac{1}{8}{P}_2+\frac{6}{8}{P}_3+\frac{1}{8}{P}_4$$

def CurvePoint(p, U, P, u):
    """
    计算 B 样条曲线上的点
    :param p: 基函数次数
    :param U: 节点矢量
    :param P: 控制点
    :param u: 固定值
    :return: 固定值 u 在 B 样条曲线上的对应值
    """
    N = BaseFunction(p, u, U)
    span = FindSpan(p, u, U)
    C = 0.0
    for i in range(p+1):
        C = C + N[i] * P[span - p + i]
    return C

四、给定点数据的全局曲线插值

假设定义一组数据点 { Q k } , k = 0 , 1 , ⋯   , n \{\pmb Q_k\},k=0,1,\cdots,n {Qk​},k=0,1,⋯,n，我们想要用一条 $p$ 次非有理 B 样条曲线插值于这些点。如果我们为每一点 $Q_k$ 指定了一个参数值 ${\overline{u}}_k$，并且选定了一个合适的节点矢量 U = { u 0 , u 1 , ⋯   , u m } U=\{u_0,u_1,\cdots,u_m\} U={u0​,u1​,⋯,um​}，我们就可以建立一个系数矩阵为 $(n+1)\times (n+1)$ 的线性方程组
$$Q_k=C({\overline{u}}_k)=\sum _{i=0}^n{N}_{i,p}({\overline{u}}_k)P_i$$

$n+1$ 个控制点 $P_i$ 是未知量，令 $r$ 是 $Q_i$ 的坐标分量的个数（一般是 2、3 或 4），则存在 $r$ 个线性方程组，它们具有相同的系数矩阵，每个方程组的解对应于一个坐标分量的设置。

剩下来的问题是如何选择 $Q_k$ 对应的参数值 ${\overline{u}}_k$ 以及节点矢量 $U$，这将影响到曲线的形状和参数化

2.1、参数值 ${\overline{u}}_k$ 的选择

假定参数都在 $u\in [0,1)$ 的范围内，通常有三种选择 ${\overline{u}}_k$ 的方法：

1. 均匀参数化：
$${\overline{u}}_0=0,{\overline{u}}_n=1,{\overline{u}}_k=\frac{k}{n},k=1,2,\cdots ,n-1$$

不推荐采用这种方法，因为当数据点分布不均匀时它会产生很奇怪的形状（例如打圈自交）。

2. 弦长参数化：令 $d$ 为总弦长
$$d=\sum _{k=1}^n\mid Q_k-Q_{k-1}\mid$$

则 ${\overline{u}}_0=0,{\overline{u}}_n=1$
$${\overline{u}}_k={\overline{u}}_{k-1}+\frac{\mid Q_k-Q_{k-1}\mid }{d},k=1,2,\cdots ,n-1$$

这是目前最常用的方法，并且一般用它就足够了

3. 向心参数化：令
$$d=\sum _{k=1}^n\sqrt{\mid Q_k-Q_{k-1}\mid }$$

则 ${\overline{u}}_0=0,{\overline{u}}_n=1$
$${\overline{u}}_k={\overline{u}}_{k-1}+\frac{\sqrt{\mid Q_k-Q_{k-1}\mid }}{d},k=1,2,\cdots ,n-1$$

当数据点急转弯变化时，这个方法能得到比弦长参数化更好的结果。

2.2、节点矢量 $U$ 的选择

1. 等距分布：即
$$\begin{array}{rl}& u_0=\cdots =u_p=0,u_{m-p}=\cdots =u_m=1\\ & u_{j+p}=\frac{j}{n-p+1},j=1,2,\cdots ,n-p\end{array}$$

不推荐采用这种方法，因为它可能导致产生奇异方程组。

2. 平均值分布：
$$\begin{array}{rl}& u_0=\cdots =u_p=0,u_{m-p}=\cdots =u_m=1\\ & u_{j+p}=\frac{1}{p}\sum _{i=j}^{j+p-1}{\overline{u}}_i,j=1,2,\cdots ,n-p\end{array}$$

这种方法节点矢量能很好地反映 ${\overline{u}}_k$ 的分布情况。

def NodeVector(p, Q):
    """
    准均匀B样条的节点向量计算
    :param p: 基函数次数
    :param Q: 数据点数组
    :return: 节点矢量
    """
    n = Q.shape[1] - 1
    d = 0.0
    for i in range(1, n + 1):  # 计算总弦长
        d += np.linalg.norm(Q[:, i] - Q[:, i - 1])
    Q_parameterize = np.zeros(n + 1)
    Q_parameterize[0] = 0
    Q_parameterize[-1] = 1
    for i in range(1, n):
        Q_parameterize[i] = Q_parameterize[i - 1] + np.linalg.norm(Q[:, i] - Q[:, i - 1]) / d

    m = n + p + 1
    U = np.zeros(m + 1)
    U[m - p:m + 1] = 1
    for i in range(1, n - p + 1):
        U[i + p] = np.sum(Q_parameterize[i:i + p]) / p
    return Q_parameterize, U

五、案例应用

例 令 { Q k } = { ( 0 , 0 ) , ( 3 , 4 ) , ( − 1 , 4 ) , ( − 4 , 0 ) , ( − 4 , − 3 ) , ( − 2 , − 5 ) , ( − 1 , − 7 ) } \{\pmb Q_k\}=\{(0,0),(3,4),(-1,4),(-4,0),(-4,-3),(-2,-5),(-1,-7)\} {Qk​}={(0,0),(3,4),(−1,4),(−4,0),(−4,−3),(−2,−5),(−1,−7)}，用三次曲线插值这些点。

完整代码如下

import numpy as np
import matplotlib.pyplot as plt


def FindSpan(p, u, U):
    """
    确定参数 u 所在的节点区间的下标
    :param p: 基函数次数
    :param u: 固定点
    :param U: 节点矢量 行向量
    :return: 节点区间的下标
    """
    m = len(U) - 1
    start, end = p, m
    if u == U[-1]:
        return m - p - 1
    while end != start + 1 and end != start:
        mid_index = (start + end) // 2
        if U[mid_index] == u:
            return mid_index
        if u > U[mid_index]:
            start = mid_index
        else:
            end = mid_index
    return start


def BaseFunction(p, u, U):
    """
    计算所有非零 B 样条基函数的值
    :param u: 固定值
    :param p: 基函数次数
    :param U: 节点矢量
    :return: 基函数值数组
    """
    i = FindSpan(p, u, U)
    N = np.zeros(p + 1)
    N[0] = 1.0
    left = np.zeros(p + 1)
    right = np.zeros(p + 1)
    for j in range(1, p + 1):
        left[j] = u - U[i + 1 - j]
        right[j] = U[i + j] - u
        saved = 0.0
        for r in range(j):
            if (right[r + 1] + left[j - r]) == 0:
                temp = 0.0
            else:
                temp = N[r] / (right[r + 1] + left[j - r])
            N[r] = saved + right[r + 1] * temp
            saved = left[j - r] * temp
        N[j] = saved
    return N


def NodeVector(p, Q):
    """
    准均匀B样条的节点向量计算
    :param p: 基函数次数
    :param Q: 数据点数组
    :return: 节点矢量
    """
    n = Q.shape[1] - 1
    d = 0.0
    for i in range(1, n + 1):  # 计算总弦长
        d += np.linalg.norm(Q[:, i] - Q[:, i - 1])
    Q_parameterize = np.zeros(n + 1)
    Q_parameterize[0] = 0
    Q_parameterize[-1] = 1
    for i in range(1, n):
        Q_parameterize[i] = Q_parameterize[i - 1] + np.linalg.norm(Q[:, i] - Q[:, i - 1]) / d

    m = n + p + 1
    U = np.zeros(m + 1)
    U[m - p:m + 1] = 1
    for i in range(1, n - p + 1):
        U[i + p] = np.sum(Q_parameterize[i:i + p]) / p
    return Q_parameterize, U


def CurvePoint(p, U, P, u):
    """
    计算 B 样条曲线上的点
    :param p: 基函数次数
    :param U: 节点矢量
    :param P: 控制点
    :param u: 固定值
    :return: 固定值 u 在 B 样条曲线上的对应值
    """
    N = BaseFunction(p, u, U)
    span = FindSpan(p, u, U)
    C = 0.0
    for i in range(p+1):
        C = C + N[i] * P[span - p + i]
    return C


if __name__ == '__main__':
    Q = np.array([[0, 3, -1, -4, -4, -2, -1], [0, 4, 4, 0, -3, -5, -7]])
    Q_parameterize, NodeVector = NodeVector(3, Q)
    A = np.zeros((Q.shape[1], Q.shape[1]))
    for i in range(Q.shape[1]):
        temp = BaseFunction(p=3, u=Q_parameterize[i], U=NodeVector)
        span = FindSpan(p=3, u=Q_parameterize[i], U=NodeVector)
        A[i, span - 3:span + 1] = temp

    Px = np.linalg.solve(A, Q[0, :])
    Py = np.linalg.solve(A, Q[1, :])
    print(A)
    print(Q[0, :])
    print(Q[1, :])

    u = np.linspace(0, 1, 1000)
    x = np.zeros(1000)
    y = np.zeros(1000)
    for i in range(len(u)):
        x[i] = CurvePoint(p=3, U=NodeVector, P=Px, u=u[i])
        y[i] = CurvePoint(p=3, U=NodeVector, P=Py, u=u[i])

    plt.plot(x, y, c='r')
    for i in range(Q.shape[1]):
        plt.plot(Q[0, i], Q[1, i], 'go', markerfacecolor='none')
    plt.show()